当我们研究某个问题的时候,该问题有很多个变量,而且某些变量与变量之间存在一定的相关关系,如果两个变量存在相关关系,那么这两个变量之间存在着重叠信息,而这就造成了数据的冗余。比如一群学生,Boy和Girl,他们的性别我们可以用二维数组来表示,对于某个学生,Boy 可表示成:[1][0],Girl可表示为[0][1],其实不必,我们可以用一维数组来表示,男生为1,女孩为0。我们为了除去一组变量的相关性,我们可以利用正交变换来把一组相关的变量转换成线性无关的变量。从原始变量中导出少数几个主成分,使它们尽可能多地保留原始变量的信息,且彼此间互不相关,由他们来代替原始变量,这就是主成分分析(PCA)。
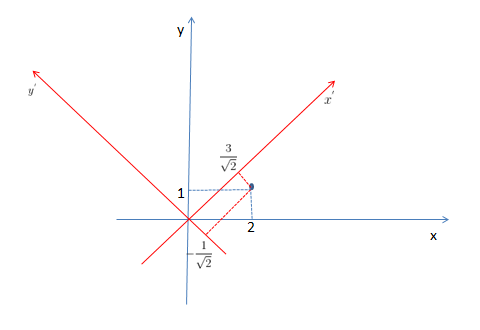
由此我们知道PCA是可以用来降低原始数据的维度的,那么怎么实现降维的呢?降维可以理解成把原始数据在一组新坐标基下表示。比如:U(2,1)这个点,在新的坐标基下的为
由此可以看出,U在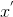
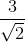
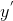

我们要对数据进行去均值,Python中mean(data, axis = 0)即可以按列求平均值,X = data-mean(data, axis = 0),即可以使得数据中心化,得:
接着刚才的问题,向每个方向投影的是不是都一样呢?不是的。我们知道方差是可以描述一维数据的,当数据在某个方向作出投影,我们可以用方差来评估这些投影后的数据,我们知道这些数据在这个方向上的分布越分散,方差越大。然而数据越分散携带的信息越丰富,因此我们可以用方差来决定向哪个方向投影比较好。在哪个方向上的方差最大,我们就选择向哪个方向投影。
不妨设向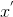
对应的方差为
由于我们之前已经去均值,则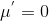
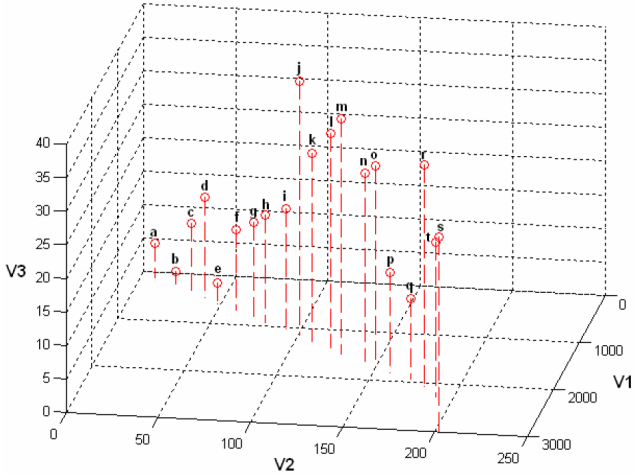
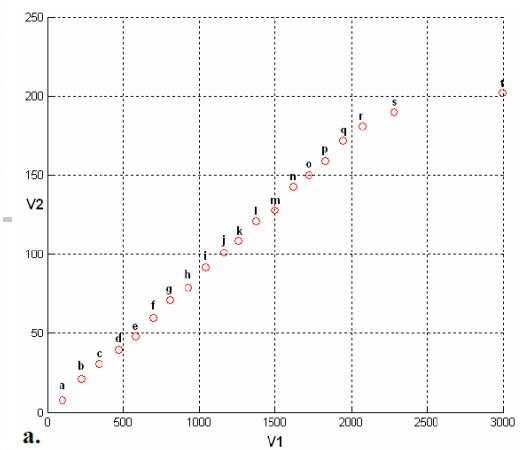
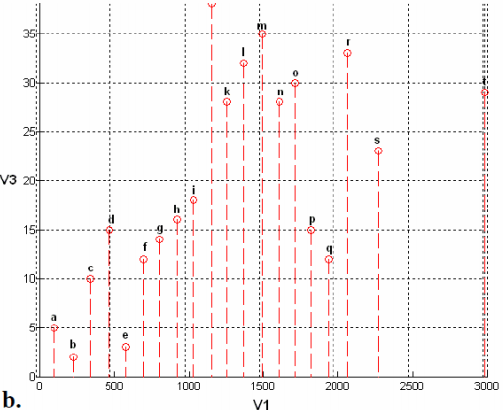
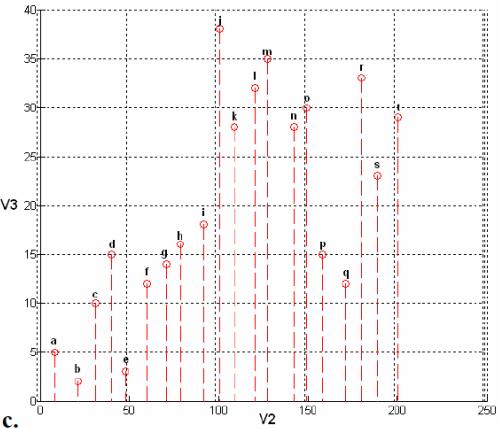
到此我们知道二维数据可以利用方差来投影,那么如果是三维数据,降到二维呢?如下所示:
我们首先同样可以利用方差,来选择一个方差最大的方向,那么这只是第一个方向,如何选择第二个呢?我们上面已经说明,我们希望得到一组线性无关的数据,假如我们继续选择方差最大的来投影,那么第二个方向将会与第一个方向几乎重合,这是我们不允许的。那么怎么办呢?我们知道考虑两个变量是否相关,有协方差可以描述。
我们知道,对于两个变量a,b,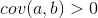
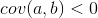
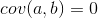
那么哪一个最好的呢?我们同样还是要利用方差的性质,即在保证所选方向是正交的之外,我们仍要保证方差尽可能的大。为了方便描述,我们仍用二维数据来描述,对于上述的X,我们有:
两端同时除以n,有:

由此,可以看出,这是一个协方差矩阵,要保证数据的不相关,就是使得该协方差矩阵相似对角化。我们知道实对称阵一定可以对角化的,而且不同特征值所对应的的特征向量一定是正交的,这些都是线代的基础知识。要保证方差最大,就可以在对角化后的对角矩阵中选取值最大特征,所对应的特征向量作为投影方向。对于n维数据,要降维到K维向量中,就选取前k大的 特征值所对应的特征向量作为新的基。由原始数据乘以新的基组成的矩阵,即为降维后的数据。
总结
PCA分为如下五步:
1,去均值
2,求原始数据的协方差矩阵
3,求该协方差矩阵的特征值特征向量
4,找出前K大的特征值所对应的特征向量,作为新的基
5,由原始数据乘以新的基组成的矩阵,即为降维后的数据。
根据如上所述,我们可以实现PCA,数据来自于http://download.csdn.net/detail/hearthougan/9664933
# -*- coding: utf-8 -*-
"""
Spyder Editor
This is a temporary script file.
"""
from numpy import *
def loadDataSet(fileName, delm = '\t'):
dataSet = open(fileName)
dataProcessed = [line.strip().split(delm) for line in dataSet.readlines()]#删除每一行的首位空格,然后按'\t'来分割
dataMatrix = matrix([map(float, line) for line in dataProcessed])#将字符串转换成浮点型
return dataMatrix
def PCA(dataMatrix, KDimesion = 9999999):
meanVal = mean(dataMatrix, axis = 0)#按列求均值
deMean = dataMatrix - meanVal
covMatrix = matrix(cov(deMean, rowvar = 0))#求且方差矩阵
eigenvalue, eigenvector = linalg.eig(covMatrix)#求特征值,特征向量
eigenvalueIndex = argsort(eigenvalue)#按从小到大排列特征值之后,返回的是每个特征值在原来特征值序列中的位置
KMaxEigenvalueIndex = eigenvalueIndex[:-(KDimesion+1):-1]#找出最大的k个特征值,对应的是k个最大的方差
selectKMaxEigenvector = eigenvector[:, KMaxEigenvalueIndex]#找出这k个特征值对应的特征向量,作为新的基
lowDimensionData = deMean * selectKMaxEigenvector#降维后的数据
reconstructionData = (lowDimensionData * selectKMaxEigenvector.T) + meanVal#重构数据
return lowDimensionData, reconstructionData
dataMatrix = loadDataSet('testSet.txt')
lowDimensionData, reconstructionData = PCA(dataMatrix, 1)
print dataMatrix
参考:蔡老师《ComputerVision_PCA_EigenFace》
张洋《PCA的数学原理》








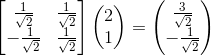
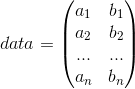
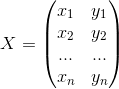
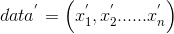
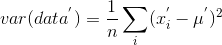
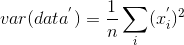
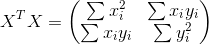













 630
630











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








