前言
前面几节讲到了深度学习采用的数据库大小为28×28的手写字,这对于机器学习领域算是比较低维的数据,一般图片是远远大于这个尺寸的,比如256×256的图片。然而特征向量的维数过高会增加计算的复杂度,像前面训练60000个28×28的手写字,在我这个4G内存,CORE i5的CPU上训练需要3个小时,如果你使用GPU当然会增加训练的速度。维数过高会对后续的分类问题带来负担,实际上维数过高的特征向量对于分类性能(识别率)也会造成负面的影响。很多人认为提取的特征维数越高对提高识别有用,然而事实并不是我们通常想的,因为一张图片中的很多特征是相关的。也就是选取合适的特征向量对提高识别率有很大的影响。因此就出现了PCA。
快速PCA算法
PCA的计算中最主要的工作是计算样本的协方差矩阵的特征值和特征向量,当然这对于MATLAB来说是非常容易的了。设样本矩阵X的大小为n×d,n代表样本的个数,d代表一个样本的特征向量。则样本的散布矩阵(协方差矩阵)S是一个d×d的方阵,当维数d较大时,如维数d=10000,那么S是一个10000×10000的矩阵,这样非常消耗内存,结果就是你的笔记本电脑卡死,CPU使用率变高,内存被占的满满的,你无法做任何其他事。这时就出现了快速PCA算法。
计算散布矩阵的特征值和特征向量,设Z为n×d的样本举证X中的每一个样本减去样本均值m后得到的矩阵,即散布矩阵S为Z'Z,S为d×d。若现在考虑矩阵R=ZZ',R为n×n,一般情况下样本目标n是远远小于样本的维数d的,R的尺寸也是远远大于散布矩阵S,然而它与S有着相同的非零特征值。
设n维列向量v是R的特征向量,则有
(ZZ')v=λv (1)
将式(1)的两边同时左乘Z',并利用矩阵乘法结合律得
(Z'Z)(Z'v)=λ(Z'v) (2)
式(2)说明Z'v为散布矩阵S=Z'Z的特征值。这说明可以计算小矩阵R=ZZ'的特征向量v,而后通过左乘Z'得到散布矩阵S=Z'Z的特征向量Z'v。
下面以剑桥大学的ORL人脸库进行试验。下面是数据库中的样本例子:
STEP 1
生成样本矩阵,大小为n×d,n代表样本个数,d代表一个样本的特征数。下面是代码。
ReadFaces.m
<span style="font-family:Times New Roman;"><span style="font-size:14px;">function [imgRow,imgCol,FaceContainer,faceLabel]=ReadFaces(nFacesPerPerson,nPerson,bTest)
if nargin==0
nFacesPerPerson=5;
nPerson=40;
bTest=0;
elseif nargin<3
bTest=0;
end
img=imread('D:\机器学习\att_faces\s1\1.pgm');
[imgRow,imgCol]=size(img);
FaceContainer=zeros(nFacesPerPerson*nPerson,imgRow*imgCol);
faceLabel=zeros(nFacesPerPerson*nPerson,1);
for i=1:nPerson
i1=mod(i,10);
i0=char(i/10);
strPath='D:\机器学习\att_faces\s';
if(i0~=0)
strPath=strcat(strPath,'0'+i0);
end
strPath=strcat(strPath,'0'+i1);
strPath=strcat(strPath,'/');
tempStrPath=strPath;
for j=1:nFacesPerPerson
strPath=tempStrPath;
if bTest==0
strPath=strcat(strPath,'0'+j);
else
strPath=strcat(strPath,num2str(5+j));
end
strPath=strcat(strPath,'.pgm');
img=imread(strPath);
FaceContainer((i-1)*nFacesPerPerson+j,:)=img(:)';
faceLabel((i-1)*nFacesPerPerson+j)=i;
end
end
save('FaceMat.mat','FaceContainer')</span></span>
利用生成的样本矩阵求特征值和特征向量。(1)先求出样本矩阵特征的平均值;(2)计算协方差矩阵;(3)计算协方差矩阵前 k 个特征值和特征向量;(4)得到协方差矩阵的特征向量然后再归一化;(5)线性变化投影到 k 维。
fastPCA.m
<span style="font-family:Times New Roman;"><span style="font-size:14px;">function [pcaA V]=fastPCA(A,k)
% A-代表样本矩阵
% k-代表降至k维
% PcaA-降维后的k维样本特征向量组成的矩阵,每一行代表一个样本,
% 列数k为降维后的样本矩阵的维数
% V-主成份向量
A=load('FaceMat.mat');
[r c]=size(A);
meanVec=mean(A);%求样本的均值
Z=(A-repmat(meanVec,r,1));
covMatT=Z*Z'; %计算协方差矩阵,此处是小样本矩阵
[V D]=eigs(covMatT,k);%计算前k个特征值和特征向量
V=Z'*V;%得到协方差矩阵covMatT'的特征向量
%特征向量归一化单位特征向量
for i=1:k
V(:,i)=V(:,i)/norm(V(:,i));
end
pcaA=Z*V;%线性变化降维至k维
save('PCA.mat','V','meanVec');</span></span>通过前两步就提取到了样本的特征向量和特征值并存储在pcaA中。
下面将介绍可视化主成份脸。V中每一列存储的是主份特征,第一列就表示存储的第一主成份,第二列表示存储的第二主成份,以此类推。
visualize_pc.m
<span style="font-family:Times New Roman;"><span style="font-size:14px;">function visualize_pc(E)
[size1 size2]=size(E);
global imgRow;
global imgCol;
row=imgRow;
col=imgCol;
figure
img=zeros(row,col);
for ii=1:20
img(:)=E(:,ii);
subplot(4,5,ii);
imshow(img,[]);
end</span></span>main1.m
<span style="font-family:Times New Roman;font-size:14px;">function main1(k)
%k代表降至k维
global imgRow;
global imgCol;
nPerson=40;
nFacesPerPerson=5;
display('读入人脸数据.....');
[imgRow,imgCol,FaceContainer,faceLabel]=ReadFaces(nFacesPerPerson,nPerson);
display('..................');
nFaces=size(FaceContainer,1);
display('PCA降维.....');
[LowDimFaces W]=fastPCA(FaceContainer,k);
visualize_pc(W);
save('LowDimFaces.mat','LowDimFaces');
display('结束.....');</span>
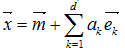
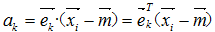

























 1029
1029

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








