题意 :
分析: 很容易可以得出:
即 :
最后可得每一项的系数为
然后可以用NTT(快速数论变换)求出每一项的系数.
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 998244353;
const ll maxn = 1e5 + 10;
ll wn[22];
ll a[maxn << 2], b[maxn << 2];
ll F[maxn], N[maxn];
ll qmod(ll a, ll b) {
ll ans = 1;
while(b) {
if(b & 1) ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
void init() {
for(int i = 0; i < 20; i++) {
int t = 1 << i;
wn[i] = qmod(3, (mod - 1) / t);
}
F[0] = 1, N[0] = 1;
for(int i = 1; i < maxn; i++) {
F[i] = F[i - 1] * i % mod;
}
N[maxn - 1] = qmod(F[maxn - 1], mod - 2);
for(int i = maxn - 1; i >= 1; i--) {
N[i - 1] = N[i] * i % mod;
}
}
void bit_reverse(int n, ll *x) {
for(int i = 0, j = 0; i != n; i++) {
if(i > j) swap(x[i], x[j]);
for(int l = n >> 1; (j ^= l) < l; l >>= 1);
}
}
void NTT(ll *a, int len, int on) {
bit_reverse(len, a);
int id = 0;
for(int h = 2; h <= len; h <<= 1) {
id++;
for(int j = 0; j < len; j += h) {
ll w = 1;
for(int k = j; k < j + h / 2; k++) {
ll u = a[k] % mod;
ll t = w * (a[k + h / 2] % mod) % mod;
a[k] = (u + t) % mod;
a[k + h / 2] = ((u - t) % mod + mod) % mod;
w = w * wn[id] % mod;
}
}
}
if(on == -1) {
for(int i = 1; i < len / 2; i++)
swap(a[i], a[len - i]);
ll Inv = qmod(len, mod - 2);
for(int i = 0; i < len; i++)
a[i] = a[i] % mod * Inv % mod;
}
}
void Conv(ll *a, ll *b, int n) {
NTT(a, n, 1);
NTT(b, n, 1);
for(int i = 0; i < n; i++)
a[i] = a[i] * b[i] % mod;
NTT(a, n, -1);
}
int main() {
init();
int n, m;
while(~scanf("%d", &n)) {
memset(a, 0, sizeof a);
memset(b, 0, sizeof b);
for(int i = 0; i <= n; i++) {
scanf("%lld", &a[i]);
a[i] = a[i] * F[i] % mod;
}
scanf("%d", &m);
int s = 0, x;
for(int i = 0; i < m; i++) {
scanf("%d", &x);
s = (s + x) % mod;
}
s = (-s + mod) % mod;
ll g = 1;
for(int i = 0; i <= n; i++) {
b[n - i] = g * N[i] % mod;
g = g * s % mod;
}
int p = 1;
while(p <= n) p <<= 1;
p <<= 1;
Conv(a, b, p);
for(int i = 0; i <= n; i++) {
a[i + n] = a[i + n] * N[i] % mod;
a[i + n] = (a[i + n] + mod) % mod;
printf("%lld ", a[i + n]);
}
printf("\n");
}
return 0;
}










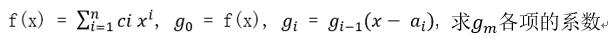
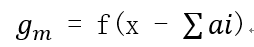
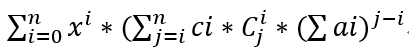
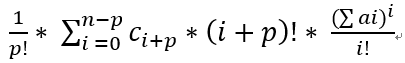














 2902
2902

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








