本人最近在看最小割/最大流的相关文章,和增广路径、压入与重标记算法相关。于是就对这两个算法进行了理解,在查看了他人的资料之后,整合之后生成了本篇文章。
增广路径(path augmentation)
思想:从任意一个可行流(如零流)出发,找到一条源s到汇t的增广路,并在该增广路上增加流值,于是得到一个新的可行流。循环此过程直到找不出s到t的新的增广路。
该算法关键是找到s到t的增广路,这可通过标号法实现,具体规则为:
· 一个节点先进行标号,再检查。一个节点可处于三个状态之一:已标号并且已检查;已标号但未检查;未标号。每次检查是从已标号的节点开始,所以设置源点s为永久标号点,当其他都未标号时,算法从已标号的源点开始。
· 一个节点i的标号表现形式由两个分量组成(+j, δ(i))或(-j, δ(i)) ,第一个分量+表示前继点,-表示后继点(即某条通过节点i的可行流的前一个节点j或后一个节点j),第二个分量表示了允许增加的流量 δ(i)=min(δ(j), cij-fij ) 。假设G(V,E) 是一个有限的有向图,它的每条边(u,v)∈E都有一个非负值实数的容量c(u,v) ;f(u,v) 是由u到v的净流。
· 从每个已标号但未检查的节点i开始,对其进行检查:检查该所相邻的所有节点j(前继点或后继点),如果存在未标号点j使得有向弧(i, j)的现有流量 fij <该弧的容量 cij ,则对该节点j进行前继标记(+i, δ(j)) 其中 δ(j)=min( δ(i), cij-fij ) ;或者存在未标号点j使得有向弧(j,i)的现有流量 fji >0,则对该节点j进行后继标记(-i, δ(j)) 其中 δ(j)=min( δ(i), fji ) 。
算法步骤:
1°. 令x=(xij)是任意整数可行流,给s一个永久标号 (*,∞);
2°. (1)如果所有标号顶点都已检查,转第4步
(2)找到一个已标号但未检查的顶点i,做如下检查:对每一条有向弧(i,j)且j未标号, 如果fij < cij 则给j标号(+i, δ(j)),δ(j)=min(δ(i), cij-fij) ;对每一条有向弧(j,i)且j未标号,如果 fji >0,则给j标号(-i, δ(j)),δ(j)=min(δ(i), fji) 。
(3)如果汇t被标记,转3°,否则转(1)
3°. 根据得到的增广路上各项标号来增加流量,并抹去除了源s外的标号转2°
4°. 此时当前流是最大流,且把所有标好点的集合记为S,(S, /S)是G的最小割。
算法的 伪代码:
1 for each edge (u, v) ∈ E[G]
2 do f[u, v] ← 0 //f[u, v]为顶点u,v之间的网络流
3 f[v, u] ← 0
4 while there exists a path p from s to t in the residual network Gf //Gf 为残留网络
5 do cf(p) ← min {cf(u,v) : (u, v) is in p} //cf(p) 为增广路径p的残留容量,cf(u,v)为边(u,v)的残留容量
6 for each edge (u, v) in p
7 dof[u, v] ← f[u, v] + cf(p)
8 f[v, u] ← -f[u, v]
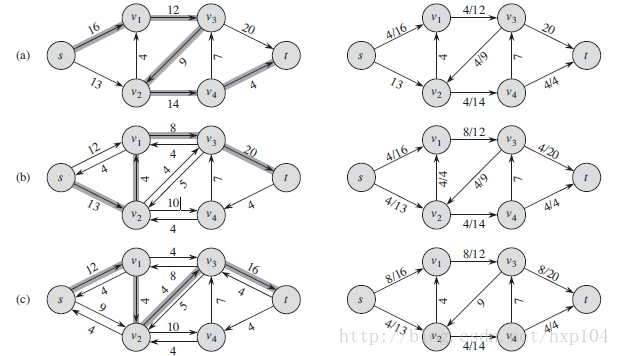
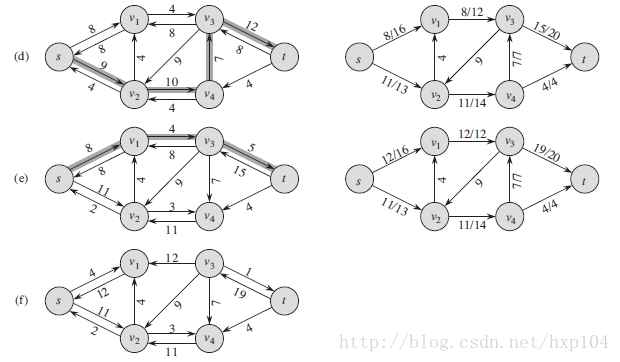
下图为实验例子的详细图解:(2个算法同为此例子)
增广路径的代码如下:
#include<iostream>
#include<math.h>
using namespace std;
#define INFI 1000
typedef struct _mark//MARK:(+j, δ(i))结构体。pre_suc:前一个连接点。max_incr:最大增量的流量即δ(i)
{
int pre_suc;
int max_incr;
}MARK;
int iteration = 0;//增广路径的次数
const int N = 100;
bool isMark[N], isCheck[N], isDone;//isMark标记。isChec检查
MARK markList[N];
int c[N][N], f[N][N];
int n; //顶点数
int min(int a,int b)
{
return a>b?b:a;
}
void Mark(int index, int pre_suc, int max_incr)//index讲标记的点。pre_suc已标记,正在检查的点
{
isMark[index] = true;
markList[index].pre_suc = pre_suc;
markList[index].max_incr = max_incr;
}
void Check(int i)
{
isCheck[i] = true;
for (int j=0;j<=n;j++)
{
if (c[i][j]>0 && !isMark[j] && c[i][j]>f[i][j])//对每一条有向弧(i,j)且j未标号, 如果fij < cij 则给j标号(+i, δ(j)),δ(j)=min(δ(i), cij-fij)
Mark(j, i, min(markList[i].max_incr, c[i][j]-f[i][j]));
if(c[j][i]>0 && !isMark[j] && f[j][i]>0)//对每一条有向弧(j,i)且j未标号,如果 fji >0,则给j标号(-i, δ(j)),δ(j)=min(δ(i), fji)
Mark(j, -i, min(markList[i].max_incr, f[j][i]));
}
}
int Maxflow()//最大流计算
{
int flow =0;
for (int i=0;i<n;i++)
{
if(isMark[i])
for(int j=1;j<n;j++)
{
if(j!=i&&!isMark[j]) flow += c[i][j];
}
}
return flow;
}
void Mincut()
{
int i = 0;
while (i<n)
{
if(isMark[i])
cout<<i<<" ";
i++;
}
}
int IncrFlowAuxi(int index)//辅助函数:计算增广路径中的最大可增量
{
if(index==0) return markList[index].max_incr;
int prev = markList[index].pre_suc;
int maxIncr = markList[index].max_incr;
return min(maxIncr, IncrFlowAuxi(prev));
}
void IncrFlow()//增广路径的增加
{
iteration++;
int incr = IncrFlowAuxi(n-1); //最大可增量
int index = n-1;
int prev;
while(index!=0)
{
prev = markList[index].pre_suc;
f[prev][index] += incr; //增广路径增加后,相应的流量进行更新
f[index][prev]=-f[prev][index];// do f[u, v] ← f[u, v] + cf(p) f[v, u] ← -f[u, v]
index = prev;
}
}
//ford_fulkerson算法
int ford_fulkerson()
{
int i;
while (1)
{
isDone = true;
i=0;
while(i<n)
{
if (isMark[i] && !isCheck[i]) //判断是否所有标记的点都已被检查:若是,结束整个算法
{
isDone = false;
break;
}
i++;
}
if (isDone) //算法结束,则计算最小割和最大流
{
Mincut();
return Maxflow();
break;
}
while (i<n)
{
if(isMark[i] && !isCheck[i])
{
Check(i);
i = 0;
}
if(isMark[n-1]) //如果汇t被标记,说明找到了一条增广路径,则增加该条路径的最大可增加量
{
IncrFlow();
memset(isMark+1, false, n-1); //增加该增广路径后,除了源s,其余标记抹去
memset(isCheck, false, n);
}
else i++;
}
}
}
int main()
{
int m, i, j,k;
cout<<"顶点个数:";
cin>>n;
cout<<"边数:";
cin>>m;
for ( k = 0; k < n; ++k)
{
memset(c[k], 0, sizeof(c[0][0])*n);
memset(f[k], 0, sizeof(f[0][0])*n); //初始各分支流量为0
memset(isMark, false, n);
memset(isCheck, false, n);
}
isMark[0] = true; //给源做永久标记
markList[0].max_incr = INFI;
markList[0].pre_suc = INFI;
cout<<"各边的数值:";
for(k=0;k<m;k++)
{
cin>>i;
cin>>j;
cin>>c[i][j];
}
cout<<"segment set S = {";
int maxflow=ford_fulkerson();
cout<<"}"<<endl;
cout<<"max flow ="<<maxflow<<endl;
return 0;
}
ps:S点为0点,其余点为1到n-1(此为本代码的缺陷,若想改可以自己改)
下面是运行的结果图:
压入和重标记算法(push-relable)
- 初始化前置流:将与源点s相连的管道流量f(0,i)设为该管道的容量,即 f(0,i)=c(0,i);将源点s的高度h(0)=V,(V表示图的顶点个数),其余顶点高度h(i)=0;将源的点余量e(0)设为源容量减去源的流出量,即e(0)=-∑f(0,i)=-∑c(0,i),与源s相连的点余量设为该点的流入量e(i)=c(0,i),其余点都为0。
- 构造一个存储顶点的队列vlist,用以检查点的压栈。从源点s出发,将与之相连的顶点压入栈(s不入栈,与s相连的点入栈)。
- 每次从栈中取首个元素,即某一个点,检查其点余量e(i),若不为0,表示要对该点进行操作——重标记或者压入流:检查与该点i全部的相邻点j,若该点比它相邻点的高度大h(i)>h(j)且该管道的容量c(i,j)大于流量f(i,j)时,将该点的余量以最大方式压入该管道delta=min(e(i), c(i,j)-f(i,j)), 点余量e、流量f相应的进行减加,另外在队列中加入满足点余量e(j)>0的相邻点j(vlist.push(j); j原不存在该队列中);若没有相邻点满足上述条件,则将该点的高度值h(i)根据相邻点j进行增加,h(i)=min(h(j))+1。以上的重标记或压入流操作循环进行,直至该点的余量e(i)为0。
- 重复第3步,直至队列vlist中没有元素,停止算法,最后输出汇点t的余量e(t), t=V-1, 该值就是最后所求的最大流。
方法的流程
1.给源点s一个足够(等于源点邻接边的容量之和)的流,流向它的邻近顶点,使它的邻近顶点构成一个活动顶点的集合A
2.遍历活动顶点集合A的每一个点v,对v进行如下操作:
(1)对v的每一条邻接边以边容量的流向前推进流(如果每条邻边都以边容量推进过的(达到最大推进),则执行(2)),并将该顶点加入集合A
(2)若(1)操作后顶点v的还有盈余量(e(v)>0),则将流量退回(逆推进)给上一个顶点(流给它的顶点),最后将v从集合A中移除,其中退回给的上一个顶点就变成了活动顶点要进入集合A
3.直到活动顶点集合A为空为止,流向汇点t的流量就是最大流量。
Push Relabel算法的流程
1)、构造初始流。将源点高度标记为n,其余点高度均为0;
2)、如果残留网络中不存在活结点,则算法结束。否则继续执行下一步;
3)、选取活结点,如果该结点出边为可推流边,则沿此边推流,否则将该节点高度增至可流向的高度值最低的点的高度值+1,执行步骤2)。
压入与重标记算法实现代码
#include <iostream>
#include <cstring>
using namespace std;
const int MAX_SIZE = 100;
const int INF = 1 << 30;
int capacityGraph[MAX_SIZE][MAX_SIZE];//即c[u][v]
int flowMap[MAX_SIZE][MAX_SIZE];//即f[u][v]
int height[MAX_SIZE];//高度h()
int excess[MAX_SIZE];//余流e()
int src, des;
int vertex_num, edge_num,account=0;//vertex_num顶点数,edge_num边数
void init()//初始设置
{
memset( capacityGraph, 0, sizeof( capacityGraph ) );
memset( flowMap, 0, sizeof( flowMap ) );
memset( height, 0, sizeof( height ) );
memset( excess, 0, sizeof( excess ) );
cout<<"输入顶点数和边数 : ";
cin>>vertex_num>>edge_num;
cout<<"各边的数值:";
for( int i = 1; i <= edge_num; ++i ){
int start, end, cap;
cin>>start>>end>>cap;
capacityGraph[start][end] = cap;
}
src = 1;
des = vertex_num;
height[src] = vertex_num;
}
void preFlow()//前置流
{
for( int i = src; i <= des; ++i ){
if( capacityGraph[src][i] > 0 ){
const int flow = capacityGraph[src][i];
flowMap[src][i] += flow;
flowMap[i][src] = - flowMap[src][i];
excess[src] -= flow;
excess[i] += flow;
}
}
}
void push( int start, int end )//压入
{
int flow = excess[start]>(capacityGraph[start][end] - flowMap[start][end] )?(capacityGraph[start][end] - flowMap[start][end] ):excess[start];
flowMap[start][end] += flow;
flowMap[end][start] = -flowMap[start][end];
excess[start] -= flow;
excess[end] += flow;
}
bool reLabel( int index )//重标记
{
int minestHeight = INF;
for( int i = src; i <= des; ++i ){
if( capacityGraph[index][i] - flowMap[index][i] > 0 ){
minestHeight = minestHeight> height[i]?height[i]:minestHeight;
}
}
if( minestHeight == INF ) return false;
height[index] = minestHeight + 1;
for( i = src; i <= des; ++i ){
if( excess[index] == 0 ) break;
if( height[i] == minestHeight && capacityGraph[index][i] > flowMap[index][i] ){
push( index, i );
}
}
return true;
}
void pushReLabel()
{
bool flag = true;
preFlow();
while( true ){
if( flag == false ) break;
flag = false;
for( int i = src; i <= des - 1; ++i ){
if( excess[i] > 0 ) flag = flag || reLabel( i );//此处每轮循环只执行一次函数reLabel( i ),当flag为TRUE时,不执行函数reLabel( i )
}
}
}
int main(){
init();
pushReLabel();
cout<<"max flow : "<<excess[des]<<endl;
return 0;
}























 1109
1109











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








