[JZOJ3401]【GDOI2014模拟】Pty爬山

Description

在Pty学校附近，有一座名之为岳之麓的高山。Pty很喜欢和（哔——）一起爬山。

山的平面模型如下：

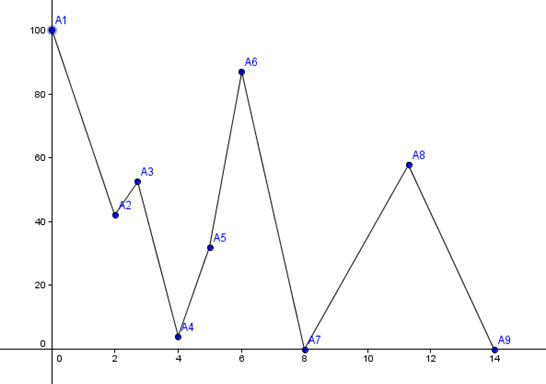
山由一个顶点集：A1,A2…An给定，保证Ai的x单调递增。我们将Ai和Ai+1之间连上线段，表示山的某一段。如下图所示：

​Pty想要爬到这座山的最高的顶点，当两个顶点的高度相同时，我们认为x比较大的顶>点要高一些。Pty不是盲人，所以他将会在爬山时采取一些策略，使得他能够尽量快的到达最高的顶点。

Pty从初始的顶点出发，往左右看去，他将朝他能够看到的最高的顶点方向走去。当走到每一个顶点时，他都会重新观察，如果这时看到的顶点比之前看到的顶点还要高，那么他将选择此时看到的顶点走去，直到他到达最高点为止。

例如上图中：Pty从A4点出发。他能够看到的最高点是A6，所以他将会向右侧走去。当他到达A5号点时，能够看到A1点比A6点更高，所以他会调转方向，向左侧走去。由于A1是最高的顶点，所以他将一直往左侧走，直到到达A1为止。

Pty想知道从每一个顶点出发，分别需要走过多少段才能到达最高点。例如上图中从A4出发需要走过5段才能到达最高点。

Solution

首先我们应求出每个点左右分别能看到的最高点是什么，分别设为$l[i],r[i]$

对于一个$i$，若$l[1]$~$l[i-1]$都已求出，画个图先

我们需要明确几点

• $i$一定能看见$i-1$
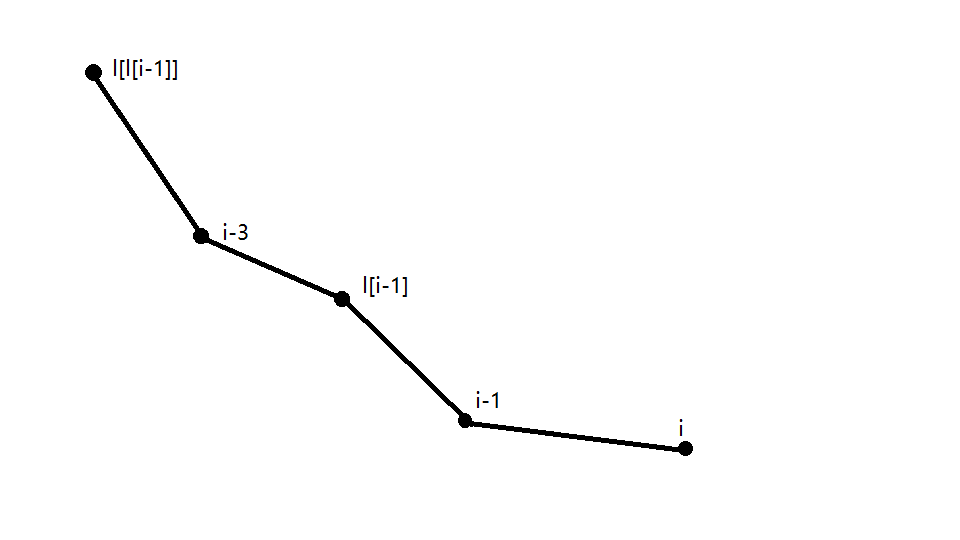
• $i$如果看不见$l[i-1]$,那么一定看不见$1$~$l[i-1]$
• $i$如果看得见$l[i-1]$且看不见$l[l[i-1]]$，那么$l[i]=l[i-1]$

为什么？

自己画一画图，推一推就出来了

有了上面的东西也就意味着，可以在$O(N)$求出所有的$l$

显然对于$r$也是一样的

现在考虑对于每个点如何求解了。

我们设$hf[i]$表示$i$能看到的最高点，$S[i]$即是它的高度。（对于$S[i]=S[j]$且$hf[i]<hf[j]$，根据题意我们需要强制使$S[j]>S[j]$）

如果我们从$i$出发，到了$j$点，而$S[j]\geq S[i]$，并且$S[i$~$j]\leq S[i]$（不包括$j$）。
那么就相当于从$i$直接到$j$,再从$j$出发。

于是可以在$i,j$之间连边

可以发现最后构成的是一棵树，跑遍最短路即可。

然后我们要想办法，对于一个$i$，快速求出它对应的$j$

可以把所有点按原来$x$坐标的顺序存入一个双向链表

按照$S$从小到大访问（排个序即可），与左（或右）端点连边，显然当前点左右任何一个点的 S <script type="math/tex" id="MathJax-Element-2100">S</script>都大于等于当前点。

于是用一种十分巧妙地方法解决。

用线段树的是SB！
用线段树的是SB！
用线段树的是SB！

Code

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cmath>
#define fo(i,a,b) for(i=a;i<=b;i++)
#define fod(i,a,b) for(i=a;i>=b;i--)
using namespace std;
struct note
{
    int h,pt,hf;    
}; 
struct note1
{
    int x,y,z;
};
bool cmp1(note x,note y)
{
    return x.h<y.h||(x.h==y.h&&x.hf<y.hf);
}
bool cmp2(note1 x,note1 y)
{
    return x.x<y.x;
}
note pt[200001];
note1 lt[200001],a[400001];
int n,x[200001],y[200001],l[200001],r[200001],a1[200001][2],bz[200001],d[2000000],dis[200001],ht;
int spfa(int l)
{
    int i,j,now;
    memset(bz,0,sizeof(bz));
    i=0;
    j=1;
    d[1]=l;
    bz[l]=1;
    dis[l]=0;
    while (i++<j)
    {
        int k;
        now=d[i];
        if (a1[now][0]>0)
        fo(k,a1[now][0],a1[now][1])
        {
            int p=a[k].y;
            if (dis[p]>dis[now]+a[k].z)
            {
                dis[p]=dis[now]+a[k].z;
                if (bz[p]==0) 
                {
                    d[++j]=p;
                    bz[p]=1;
                }
            }
        }
        bz[now]=0;
    }
}
bool pd(int u,int v,int k)
{
    double x1=(y[u]-y[k])*1.0/(x[u]-x[k]),x2=(y[v]-y[k])*1.0/(x[v]-x[k]);
    if ((u>v&&x1>=x2)||(u<v&&x1<=x2)) return 1;
    else return 0;
}
int main()
{
    freopen("climb.in","r",stdin);
    freopen("climb.out","w",stdout);
    cin>>n;
    int i,j,mx=0;
    fo(i,1,n)
    {
        scanf("%d%d",&x[i],&y[i]);
        if (y[i]>=mx)
        {
            mx=y[i];
            ht=i;
        }
    }
    l[1]=0;
    r[n]=n+1;
    fo(i,2,n)
    {
        j=n-i+1;
        l[i]=i-1;
        while(y[l[i]]<=y[l[l[i]]]&&pd(l[l[i]],l[i],i)&&l[i]!=1) l[i]=l[l[i]];
        r[j]=j+1;
        while(y[r[j]]<=y[r[r[j]]]&&pd(r[r[j]],r[j],j)&&r[j]!=1) r[j]=r[r[j]];
    }
    fo(i,1,n) 
    {
        int hf;
        hf=(y[r[i]]>=y[l[i]])?r[i]:l[i];
        lt[i].x=i-1;
        lt[i].y=i+1;
        if (i==ht) 
        {
            pt[i].h=1802201963;
            pt[i].pt=i;
            continue;
        }
        pt[i].h=y[hf];
        pt[i].hf=hf;
        pt[i].pt=i;
    }
    sort(pt+1,pt+n+1,cmp1);
    fo(i,1,n-1)
    {
        int p=pt[i].pt,hf=pt[i].hf;
        if (hf>=p)
        {
            a[2*i-1].x=p;
            a[2*i-1].y=lt[p].y;
            a[2*i-1].z=abs(p-lt[p].y);
        }
        else 
        {
            a[2*i-1].x=p;
            a[2*i-1].y=lt[p].x;
            a[2*i-1].z=abs(p-lt[p].x);
        }
        a[2*i].x=a[2*i-1].y;
        a[2*i].y=a[2*i-1].x;
        a[2*i].z=a[2*i-1].z;
        lt[lt[p].x].y=lt[p].y;
        lt[lt[p].y].x=lt[p].x;
    }
    sort(a+1,a+2*n-1,cmp2);
    fo(i,1,2*n-2)
    {
        if (a[i].x!=a[i-1].x)
        {
            a1[a[i-1].x][1]=i-1;
            a1[a[i].x][0]=i;
        }
    }
    a1[a[2*n-2].x][1]=2*n-2;
    memset(dis,107,sizeof(dis));
    spfa(ht);
    fo(i,1,n) printf("%d\n",dis[i]);
}