Description
Bessie has gone to the mall's jewelry store and spies a charm bracelet. Of course, she'd like to fill it with the best charms possible from theN (1 ≤ N ≤ 3,402) available charms. Each charm i in the supplied list has a weightWi (1 ≤ Wi ≤ 400), a 'desirability' factorDi (1 ≤ Di ≤ 100), and can be used at most once. Bessie can only support a charm bracelet whose weight is no more thanM (1 ≤ M ≤ 12,880).
Given that weight limit as a constraint and a list of the charms with their weights and desirability rating, deduce the maximum possible sum of ratings.
Input
* Line 1: Two space-separated integers: N and M
* Lines 2..N+1: Line i+1 describes charm i with two space-separated integers:Wi and Di
Output
* Line 1: A single integer that is the greatest sum of charm desirabilities that can be achieved given the weight constraints
Sample Input
4 6 1 4 2 6 3 12 2 7
Sample Output
23
这道题的POJ测试网址:http://bailian.openjudge.cn/practice/4131/
如果不能提交就注册账号并且加入小组即可
先贴代码为敬:
CODE
#include<iostream>
#include<algorithm>
#define MAX 3403
int w[MAX], d[MAX], c[12888];
int main(){
int n, m;
while (std::cin >> n >> m){
for (int i = 0; i < n; i++){
std::cin >> w[i] >> d[i];
}
for (int i = 0; i <= m; ++i){c[i] = 0;}
for (int i = 1; i <= n; ++i){
for (int j = m; j >= 0; --j){
if (j - w[i - 1] < 0){continue; }
c[j] = std::max(c[j],(c[j - w[i - 1]] + d[i - 1]));
}
}
std::cout << c[m] << std::endl;
}
return 0;
}
这道题是经典的动态规划中的背包问题,可以百度背包九讲,dd大神有非常精彩的讲解。我的总结是参考那篇文章后自己做的一个更精简的总结,希望对大家理解有所帮助
状态转移方程:
wi代表i物品的消耗,vi代表其价值
m(i, j) 代表使用了前i件物品,在背包上限为j的情况下,取到的最大总价值
问题归纳:
一共有n件物品,每件物品的费用为c[i], 价值为w[i],
F[i][v]代表使用前i个物品放入费用上限v的背包,得到的最大价值
循环体:
For I = 1:n
For v = M..0 或者 0..M
F[i][v] = max(F[i – 1][v], F[i – 1][v –c[i]] + w[i]), --------转移方程时间复杂度为n*M,不可以优化空间复杂度为n*M,可以优化为M:
利用F[v]代替F[i][v],因为转移方程中:F[i][v]完全依赖于F[I – 1][v],按照i = 1...n的顺序,计算出i-1下所有的F[i - 1][v],再计算F[i][v]
CASE 1:如果每个物品只能取一次
For I = 1..n
For v = M..0 ---------计算f[x]时保证f[v)(v<x)的结果与c[i],w[i]无关。也就保证F(i)计算结果来源与F(I –1)
F[v] = max(F[v], F[v – c[i]] + w[i])时间复杂度为O(n*M),空间复杂度优化为O(M)
CASE2:如果每个物品可以取无限次
For I = 1..n
For v = 0..M ---------计算f[x]时保证f[v)(v<x)的结果已经和c[i],w[i]有关。想象到有一个w[i]/c[i]最大即性价比最高的物品,重复被使用。
F[v] = max(F[v], F[v – c[i]] + w[i])时间复杂度为O(n*M),空间复杂度为O(M)
CASE3: 如果每个物品最多只能取x次
思路一
1. 首先确定i物品的使用次数上限,n[i]= min(x, M/c[i])。物品i能被使用的上限肯定不能超过x次也不能使得n[i]*c[i]超出背包上限M。
2.case1中
For I = 1..n
For v = M..0 ---------计算f[x]时保证f[v)(v<x)的结果与c[i],w[i]无关。也就保证F(i)计算结果来源与F(I – 1)
F[v] = max(F[v], F[v – c[i]] + w[i]) 如果c[i]和w[i]可变,那么我们在I 和 v 固定的情况下,循环测试(k*c[i], k*w[i]), k = 0到n[i],即把case1中
F[v] = max(F[v], F[v – c[i]] + w[i])
换为
For k = 0…n[i]
F[v] = max(F[v – k*c[i]] + k*w[i]) 时间复杂度V(M*Σn[i]),空间复杂度O(M)
思路二:
1.先确定使用次数上限n[i] =min(x, M/c[i])。
2. 然后n[i]拆分成一个不重复的数组,例如n[i] = 13,1 2 4 6,前面为2的等比数列,最后一个数使得数组总和为n[i],
这是为了利用选中数组的任意几个,用尽量短的数组来构成0到n[i]。这样将物品(c[i], w[i])变为4个物品,(c[i], w[i]), (2[ci], 2w[i]), (4c[i], 4w[i]), (6c[i],
6w[i]), 这样可以用一个4位2进制代表拆分后的物品是否被选择,可以用于表示到底选中了多少个c[i],例如(0, 0, 0, 1)代表选择了最后一个,用了6个
n[i], (1,0,1,0)代表选了5个n[i]。
3. 这样i物品拆分成a[i]个物品,a[i] = log2(n[i])+ 1
4. 把1-n到物品,转变为Σa[i]个物品,然后对这Σa[i]的物品做case1的算法
复杂度计算: 把case1的n换成Σa[i],是O(Σlog(n[i]))
时间复杂度优于思路一,为O(M*Σlog(n[i])),空间复杂度为O(M)
CASE 4 组合问题
1. N个物品有的只能选一次,有的无限次,有的有限次,那么组合问题的解法就是先按照case3的思路2,把有x次选择上限的物品i扩展成a[i]个新物品,这些新物品也只能最多选一次
2. 遇到物品只能选一次的,case1算法第二层循环v应按M…0循环
3. 物品可以选无限次的,第二层循环v应按0…M
4. 这样任何组合背包问题都可以归为CASE1和CASE2的结合体解决
CASE 5 依赖问题(比较难)
题设:F[i][v]代表使用前i个物品放入费用上限M的背包,得到的最大价值
N为物件总数,每个物品可以使用有限次。
新约束条件是:选择了i物品,j物品必须选择,我们称i依赖于j。而j物品可以单独选择
思路:
1. 先确定主件和附件的概念:我们说j 为附件,i 为主件,选择了i则肯定有选择j,但是j可以选择任意。因此选项有:
选择一件主件+一件附件,选择一件主件后选择2个附件,一个主件+3个附件,这里控制变量,主件只选一个。
不选主件+不选附件,不选主件+一个附件, 不选主件+2个附件
所以我们可以把选择x1个主件,x2个附件的所有情况算出来,把最后cost相同,保留weight综合最大。这样就形成了一个物品组
这样做的前提是没有连续的依赖,比如i<-j<-k,一个附件不会同时依赖两个主件。
得到一个关于主附件的物品组,利用CASE4的思路一解决。
2. 关键在于最快求得物品组:
最简单莫过于选了x1个主件i,附件j则为x2 = x1 .. MAX, 其中MAX = min(n[j], (M– x1*c[i])/c[j]). 把所有的结果都遍历一次就可以求得物品组
更好的办法是: 主件i上限为n1, 附件j上限为n2, 把n1 和 n2都展开成序列。
假设有n1:13, n2 :8, 展开为 1 2 46 1 2 4 1. 把n1确定为1,构成4个(n1, n2):(1,1),(1,2),(1,4)(1,1),用做一个01背包问题,快速 求得至少有一个主件的情况下,求得v = 1…M的F’[v]。
在上诉结果中,再计算没有一个主件,全为附件的情况,看是否比原来的F’[v]更大,更新计算出的F’[v]。计算注意主件的使用上限。
至此计算出主件和附件组成的物品组,利用CASE4的思路二解决。
动态规划问题的解法总结
1. 把原问题分解为若干个子问题,子问题和原问题形式相同或类似,只不过规模变小了。
子问题的解一旦求出就会被保存,所以每个子问题只需求解一次。
2. 将答案的解,通过某个状态值表示,比如这道题目,状态就是(使用前i个物品,背包费用上限),值:当前背包上限下能取得最大的价值
3. 递归地(动态规划)把求优大问题分解为子问题中取最优
4. 计算出初始值,按照一定的顺序遍历所有的状态,制作记忆体存储已经得到状态值,避免重复计算
5. 大问题转为小问题时的状态转移函数,可以有多种递推方式,人人为我(从问题末端除法,大问题为子问题去优,进而计算子问题),我为人人(从基础子问题除法,递推计算大问题)
能用动规解决的问题的特点:
1) 问题具有最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质。
2)无后效性。当前的若干个状态值一旦确定,则此后过程的演变就只和这若干个状态的值有关,和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态,没有关系。
如果当前的(状态---解)的选择不具备无后效性,则可以考虑增加状态的维度,如一个状态值变为2个状态值,来使得局部子问题最优解具有无后效性。
有所帮助:










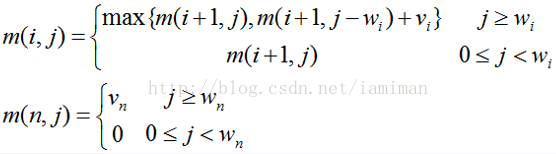













 251
251











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








