SVM(support vector machine,支持向量机)是最好的分类模型之一。通过寻找高维空间上的超平面,把样本分隔为两类,并且计算复杂度并没有因为高维映射而增加。
间隔
在logistic回归中,通过logistic函数,我们得到介于[0,1]之间的预测值h(x)。h(x)>0.5,判定为正类,反之判定为负类。在建立概率模型时,我们把h(x)大小当做x属于正类的概率,即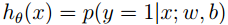
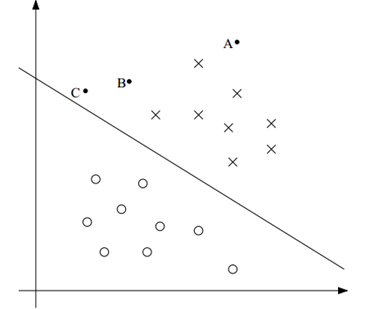
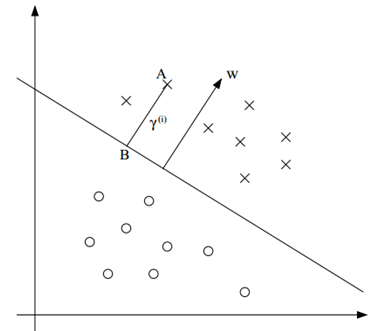
直观地,我们观察下面这幅图:
在二维空间中,以一条直线分隔两类样本。其中A远离分界面,C靠近分界面。我们直观地感觉A属于这一类的可能性会大于C。
于是,在分类建模是,我们会希望寻找一条分隔线,在所有样本分隔正确的同时,使所有样本尽可能远离分隔线。我们称这条分隔线为最小间隔平面,也就是我们希望得到的最优分类器。下面具体定义间隔。
函数间隔
在线性分类中,我们定义如下的一种间隔:
Y属于[-1或1],
Wtx+B项是线性拟合函数,类似logistic回归中得到的h(x)值,越大,属于正类的可能性越大。
如果分类正确,y与wtx+B同号,置信度为正,且越大,置信度越大。
如果分类错误,那么得到一个负值。这种间隔称为函数间隔。
那么,得到这么一个结论:函数间隔越大,样本正确分类置信度越大。
于是,在寻找最优分割平面时,我们可以以最小化函数间隔为目标建模。
缺点:我们直接把w变为2w,b变为2b。那么得到的预测值
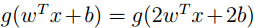
我们可以设:
||w||=1或者用
几何间隔
我们用更直观的方法来定义间隔,如下:
直接用点到直线的欧式距离来定义间隔。根据几何知识,我们可以写出几何间隔的公式:
可以看出,如果||w||==1,几何间隔就变为函数间隔。
最大间隔分类器
现在定义一种线性分类器,其寻找一条最大几何间隔的分隔平面。根据上面函数间隔的定义,我们可以得到这种分类器的最优化式子:
其中r表示函数间隔,约束为所有的样本的函数间隔都大于这个最小间隔,||w||=1为函数间隔归一化约束。
上述的最优化问题中,||w||=1是非凸域,所以上式是一个非凸优化问题。我们转而最大化几何间隔,就可以去掉归一化非凸约束,得到:
R还是函数间隔,不过现在目标函数维最小化几何间隔,并且目标函数是非凸的。
考虑到我们可以随意给w,b一个约束来归一化,而不会改变结果。也就是我们可以随意改变几何距离的量纲。这里,我们假设最优的函数间隔r=1,再把max改写成min,得到:
终于,得到了一个二次凸规划问题(QP),可以用简单的最优化算法求得最优解。
拉格朗日对偶规划
上述解得最优解,我们得到在当前空间上的最优分隔面。当时之前说过,SVM是在高维空间上的最优分隔平面。我们通过下面的方法,得到这种高维映射。
考虑一般的最优化问题:
我们可以写出其拉格朗日乘子,得到:
根据等式约束最优性条件,解:
最后能够得到原最优化问题的最优解。
关于不等式约束问题:
接下来我们要通过一定的变换,得到上述优化问题的等价形式,也就是其对偶规划。
写出拉格朗日乘子:
我们考虑下面这个优化问题:
也就是
观察上面的问题,如果w不满足约束,也就是
这里的变量是alfa,beta,那么第一项是常数不变,第二项为正数*alfa,第三项为非零*beta。那么,这个最优化问题最大值为正无穷。
当w满足约束,也就是
考虑到附加条件alfa>=0,于是其最大值只有在alfa=0时得到,后两项均为0。于是,上式等价于:
也就是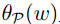
于是,有约束问题我们通过如上的方法,写成无约束形式,如下:
我们直接交换min,max顺序,得到称为对偶规划的形式,如下:
原约束最优解为P*,对偶问题的最优解为d*。一般的,关于对偶问题,有:
Min max>=maxmin;
一个简单的比喻就是:一群胖子中的最瘦的会大于一群瘦子中最胖的。
于是我们有:
经证明,在一定条件下,上面的式子取等号。也就是传说中的KKT条件:
其中的条件:
称为KKT互补条件。也就是alfa,g至少有一个为0。
小结:不等式优化问题可以写成无约束问题,无约束问题可以再写出其对偶规划问题。在KKT条件下,原问题与对偶问题有相同的解。于是,我们可以在KKT条件下,解对偶问题,得到原问题的解。
对偶规划运用于SVM问题
通过之前的推导我们得到SVM的最优化形式:
支持向量的来源
上式写出其拉格朗日乘子的话,有乘子项:
根据KKT互补条件,只有一部分的gi(W)的系数alfai!=0,仅当g(w)=0,也就是这些样本的几何间隔为1。也就是在求解的过程中,只有这部分对于最后的结果有影响。
直观来看,如下图:
无论其他点如何,最优的分割面只由最接近的三个样本点决定,这些也就是SVM的支持向量。
继续上面的推导,我们写出SVM优化的拉格朗日乘子:
写出KKT条件的两个条件 :
以及:
带回到拉格朗日乘子中,得到包含部分KKT条件的拉格朗日乘子形式:
*上面的步骤中,我们通过部分的KKT条件,用其他的变量表示w。
再根据对偶规划理论,以及剩余的KKT条件,得到如下的对偶问题:
其约束为对偶KKT条件的附加项。有了附加KKT条件,对偶规划的解也就是原规划的解。
*至此,原优化问题完全等价于上面的优化问题。
解上述问题后,我们得到最优的alfa,再通过之前KKT的条件,我们可以解出w与b :
预测分类时,当一个测试样本输入时,我们如下计算:
也就是任意一个测试样本,都要与所有的训练样本求内积。由此我们引出核方法来简化计算。
核方法
对于一个样本,我们可以写出其高维组合,如下:
有这么一种函数K(X,Z),其结果为X,Z高维投影后的内积,也就是:
我们称之为核函数。
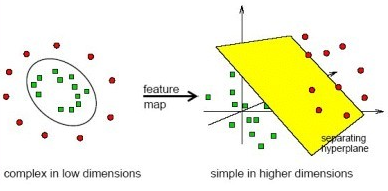
先假设我们有这样的函数,并且其计算时间复杂度很低。那么上面的SVM中,我们直接用核代替所有的内积,就能够得到样本高维投影的高维空间最优分隔平面。由于许多样本是线性不可分的,但是投影到高维空间后,却可以更好地寻找一个线性分隔面。如下:
以简单的线性核函数为例子阐述如下:
而考虑高维点积如下:
即核函数结果等于高维内积。
在考虑其时间复杂度:
核函数第一步的计算为N为向量点积后得到实数相乘,复杂度为O(N)。
高维投影后,两个N^2的向量点积,时间复杂度为O(N^2)。
也就是说,我们通过核函数,用低维的计算量得到了高维的结果,没有增加计算复杂度的同时,得到了性质更好的高维投影。也就是kernel trick。
Mercer定理
那么,怎样的函数,得到的结果会是原向量的高维内积呢?如下推导核函数的Mercer定理。
对于给定的任意向量集合:
核矩阵定义为任意两个向量核函数组成的矩阵,也就是:
对于任意的矩阵z,根据内积的非负性,我们有:
也就是说,K如果是核函数,那么对于任意的样本集合,得到的核矩阵为半正定矩阵。








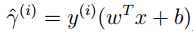
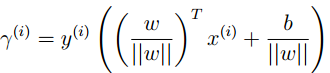
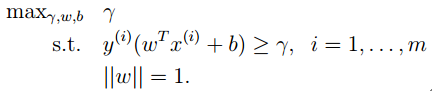
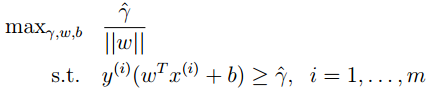




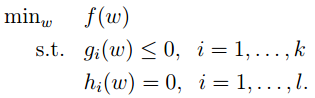

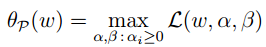
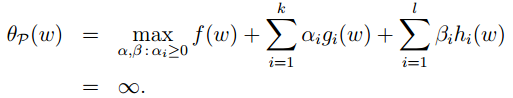
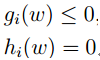
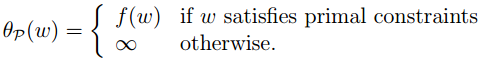



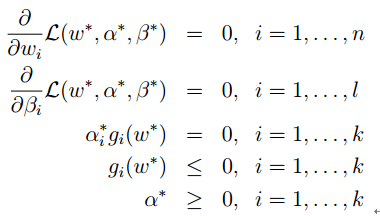

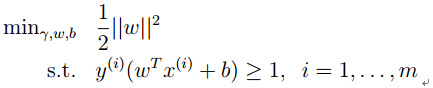



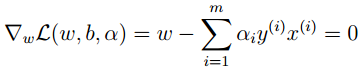

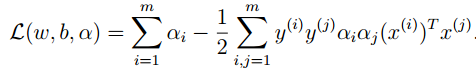
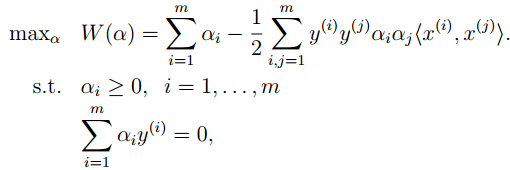
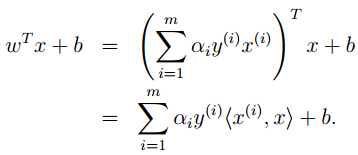

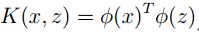
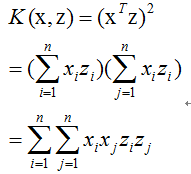
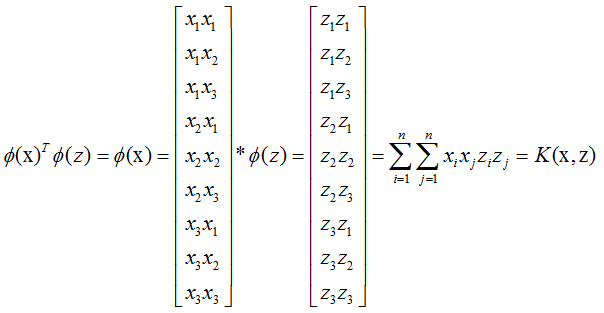


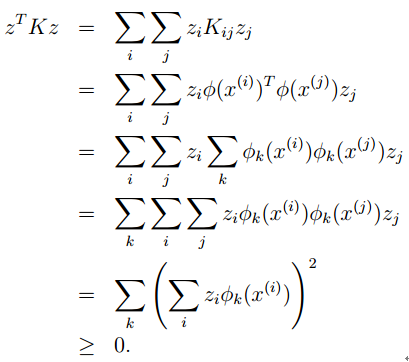













 4498
4498











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








