SVM(Support Vector Machine)读书笔记一（最佳分割超平面）

背景

分类问题中，在一个线性不可分的样本上，通常需要用到一些Non-linear的特征，把低维度空间上的样本投影到高维度上，从而使得这些样本在高维度线性可分。但是这个投影的过程通常也会有以下两个问题：

1. 如果在原样本中加了太多的高次多项式的特征，首先会导致过拟合，模型的泛化能力会很差；
2. 多项式组合会有指数级别的组合方式，这使得在投影后的样本空间中维度非常高，这也会消耗太多的计算资源和空间资源

为了解决上面两个问题，于是诞生了SVM，SVM有如下两个优势：

1. 首先SVM是基于结构风险最小化原理，即它的VC维很小（相比于它的维度），不容易导致过拟合；（VC维是衡量模型复杂度的一个指标，VC维越大说明hypothesis空间越大，越不容易得到一个理想的模型，它和train error一起决定了泛化误差的上限）。
2. 其次，利用SVM的优化过程，可以利用kernel trick，把在高纬度空间中的计算放到低纬度空间来进行，因此可以把SVM的特征投影到高纬度甚至无穷维，并且消耗很小的计算和存储资源。

接下来来介绍SVM是怎么工作的，以及它为什么有上面两个优势。本节主要介绍最佳分割平面及其求解过程以及为什么它是最佳的。

最佳分割超平面

现在假设有两类线性可分的样本，一类圈圈，一类叉叉。分类问题就是要找一个超平面，将这两类分开，但是能分割开这两类的超平面有很多，如下面的图所示。感知机算法就是随机的找到一个能够分开的超平面，它并不关心这个超平面如何。下面三个图中，直觉上感觉，第三个超平面是最理想的。

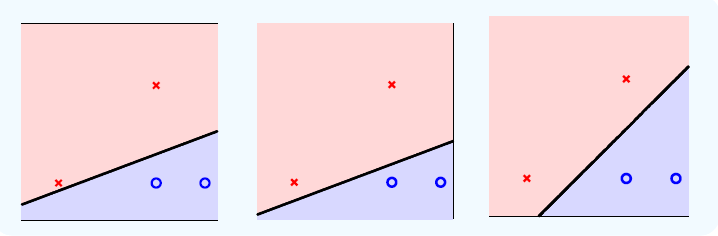
那么为什么第三个超平面是最理想的呢？原因是测试集上的样本是我们观测得到的数据，而观测到的数据和它真实分布是有一定的误差的，下面三个图中灰色的圆圈表示了每个平面能够容忍误差的大小，当误差超过这个圆圈的范围，分割面就要犯错误了，所以第三个图的容忍误差的能力是最强的。这是从直观上的一个解释，下面推导SVM的过程中会解释为什么这个是最佳的分割面。

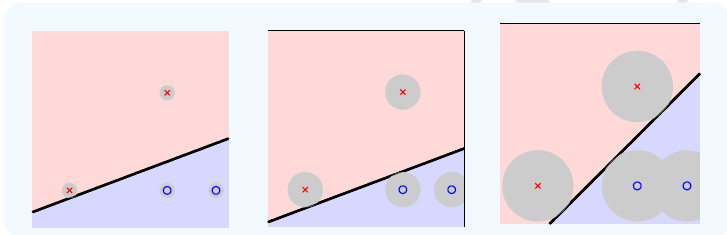
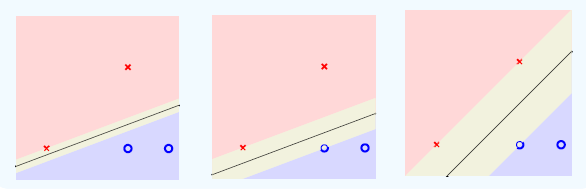
这样，能容忍误差的能力最大的那个超平面是我们要的，定义margin为，由分割平面开始往两边推，到碰到样本点时候的距离。如下面的图所示，黄色部分即为margin。

最佳分割平面求解

符号定义如下，其中$x$和$w$是属于$d$维空间中的点，$b$是超平面的偏差，h是目标求解的hypothesis。

$$x = \left[ \begin{array}{c} x_1\\ x_2\\ ...\\ x_d \end{array} \right]; w = \left[ \begin{array}{c} w_1\\ w_2\\ ...\\ x_d \end{array} \right];b=bias; h(x)=sign(w^Tx+b)$$

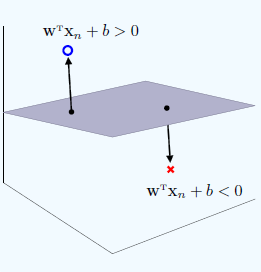
如果一个超平面可以完全把正负类样本分开，那么分布在超平面两侧的样本点表示成下图中的形式，那么所有样本可以用公式归纳成

$$y_n(w^Tx_n+b)>0, n=1,2...N$$ .
假设 $\rho=\underset{n=0,1...N}{min} y_n(w^Tx_n+b)$, 如果能够完全分开，则 $\rho>0$。然而在 $w^Tx+b=0$这个超平面上，对 $w$做一下scaling，即乘以或除以一个大于零的数，这个平面是不会变的。那么如果上式中对 $w$做一个除以 $\rho$的scaling,得到如下：
$$\rho/\rho=\underset{n=1...N}{min} y_n(w^Tx_n+b)/\rho=1$$
因此， $y_n(w^Tx_n+b)>0, n=1,2...N$和 minn=0,1...Nyn(wT