题目:同伦法(Homotopy Method)
学习压缩感知重构算法,经常能见到同伦法,但这里首先要特别说明的是,今天这里讨论的同伦法仅仅是一种思想,而不是一个具体的算法,类似于Majorization-Minimization优化框架。
1、同伦的基本原理
首先看一下同伦的基本原理【1】:
这里说的比较专业,直接简单一点,例如,令
注意,此时H(x,0)=f(x),而H(x,1)=g(x),满足上面的式(3-31),因此H(x,s)就是一条连接f和g的路径。
2、牛顿迭代与同伦法
单纯知道了同伦法的思想是不够的,下面参考【2】举一个同伦法与牛顿迭代法[3]相结合的应用实例,以更好的消化同伦法的思想。
2.1牛顿迭代法
在我的印象中,首次见到牛顿迭代法是在大一时学C语言,谭浩强的教材里有一道题是让编写一个牛顿迭代的C语言程序。以下参考【3】简单介绍一下牛顿迭代法。
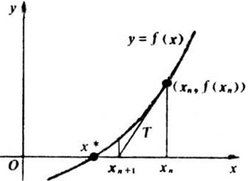
牛顿迭代法(Newton's method)又称为牛顿-拉夫逊(拉弗森)方法(Newton-Raphsonmethod),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。牛顿迭代法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。如下图所示,若要求解方程f(x) = 0的根,即求解y=f(x)与x轴的交点x*:
设x*是f(x) = 0的根,选取x0作为x*的初始近似值,过点(x0,f(x0))做曲线y=f(x)的切线L,根据初中学过的知识很容易得出L的方程为(已知直线斜率和线上的一个点)
令y=0,求出L与x轴交点的横坐标
称x1为x*的一次近似值。过点(x1,f(x1))做曲线y=f(x)的切线,并求该切线与x轴交点的横坐标
称x2为x*的二次近似值。重复以上过程,得x*的近似值序列,其中
称为x*的n+1次近似值,上式称为牛顿迭代公式。
下面通过一个例子来说明牛顿迭代法的应用。
已知f(x)=ex-1,求方程f(x) = 0的根。(这个例子很简单,不用求也知道方程的根为x=0。)
牛顿迭代法需要函数的导数,因此首先编写两个函数:
1)func.m(即f(x))
function y = func(x)
y = exp(x)-1;
end2)func_g.m(即f (x)的导数)
function y = func_g(x)
y = exp(x);
end下面给出牛顿迭代的函数代码:
3)NewtonIter.m
function [x] = NewtonIter(x0,f,g,tol,verbose,EnPlot,neg_in,pos_in,step_in)
% Version: 1.0 written by jbb0523 @2016-08-23
% 牛顿迭代法函数
% x0为初值, f为目标求解函数, g为f的导数
% tol为精度要求,verbose和EnPlot控制是否输出迭代过程
% x为输出最终解
% 参考文献:1)百度百科:牛顿迭代法
% 2)http://blog.sina.com.cn/s/blog_86186c970102vll8.html
if nargin < 9
step_in = 0.05;%默认绘图步长
end
if nargin < 8
pos_in = 3;%默认绘图上限
end
if nargin < 7
neg_in = -3;%默认绘图下限
end
if nargin < 6
EnPlot = 0;%默认不输出迭代过程(figure)
end
if nargin < 5
verbose = 0;%默认不输出迭代过程(Command Window)
end
if nargin < 4
tol = 1e-3;
end
if EnPlot
neginf = neg_in;posinf = pos_in;step = step_in;
X_Plot = neginf:step:posinf;
figure;plot(X_Plot,f(X_Plot),'r');
grid on;hold on;pause;
end
iter = 0;
x = x0;
if verbose
fprintf('Iter %d: x=%f,f(x)=%f\n',iter,x,f(x));
end
if EnPlot
Y_Plot = f(x) + g(x)*(X_Plot-x);%切线方程
plot(X_Plot,Y_Plot);
hold on;pause;
end
while abs(f(x)) > tol
x = x - f(x)/g(x);%牛顿迭代公式
iter = iter + 1;
if verbose
fprintf('Iter %d: x=%f,f(x)=%f\n',iter,x,f(x));
end
if EnPlot
Y_Plot = f(x) + g(x)*(X_Plot-x);%切线方程
plot(X_Plot,Y_Plot);
hold on;pause;
end
end
if verbose
hold off;
end
end4)Test.m
close all;clear all;clc;
x0 = 5;
x =NewtonIter(x0,@func,@func_g);
fprintf('x=%f\n',x)运行Test.m后,最终输出结果为x=0.00015,这是由于NewtonIter.m中的精度参数tol默认为10-3,若想提到x的精度,请修改tol的值。
特别注意,这里说的牛顿迭代法并不是最优化方法中的牛顿法,若要学习最优化方法中的牛顿法,参见博客http://blog.csdn.net/itplus/,该博客中作者用了五篇详细说明了从牛顿法到拟牛顿法的一系列问题[4]。
2.2牛顿迭代法的不足
牛顿迭代法需要输入一个初值x0,然而这个初值有时并不好选,选的不合适还会造成迭代不收敛,以一个例子来说明。
已知f(x)=arctan(x),求方程f(x) = 0的根。(这个例子也很简单,不用求也知道方程的根为x=0。)
跟前面一样,首先编写两个函数:
1)fx.m(即f(x))
function y = fx(x)
%f(x)=arctan(x)
y = atan(x);
end2)gx.m(即f (x)的导数)
function y = gx(x)
%g(x)=1/(1+x^2)
y = 1./(1+x.^2);
end3)Test.m
close all;clear all;clc;
x0 = 5;
x =NewtonIter(x0,@fx,@gx,1e-3,1,1);
fprintf('x=%f\n',x)我们发现输出结果为x=NaN,并没有得到方程的根,这是因为由于初值选的不合适,而这个函数又有其特殊之处,因此最终迭代未收敛。文献【2】指出,若初始值
则迭代就会发散。可以在测试程序中将x0=1.3,则可以得到输出结果为x=-0.000026。
2.3 将同伦法应用于牛顿迭代
文献【2】指出,同伦法可以用来帮助牛顿迭代产生一个好的初始值:
构建函数F0(x)和H(x,s):
则函数F0(x)与F(x)同伦,同伦路径为H(x,s)。寻找一个满足条件函数F0(x)很简单,例如:
其中x*是一个给定的起始值,把x=x*代入F0(x),则有F0(x*)=0 。将F0(x)代入H(x,s)得:
将同伦法应用于牛顿迭代工作流程如下:
因此,为了“已知f(x)=arctan(x),求方程f(x) = 0的根”,我们编程如下:
1)Hxs.m(即H(x,s))
function y = Hxs(x,s,x0)
%H(x,s)=arctan(x) +(s-1)*arctan(x0)
y = atan(x) + (s-1)*atan(x0);
end2)gx.m(与前面一样,因为H(x,s)相比于f(x)只加了一个常数,其导数不变)
function y = gx(x)
%g(x)=1/(1+x^2)
y = 1./(1+x.^2);
end由于应用同伦法函数H(x,s)除了参数x还要输入s和x0,这就需要牛顿迭代函数需要相应的改变。
3)NewtonIterHomo.m(专门用于同伦法的牛顿迭代函数)
function [x] = NewtonIterHomo(x0,Hxs,gx,s,tol,verbose)
% Version: 1.0 written by jbb0523 @2016-08-21
% 专门用于同伦方法的牛顿迭代法函数
% 目标函数:H(x,s)=arctan(x) + (s-1)*arctan(x0)
% x0为初值, Hxs为目标求解函数, gx为Hxs的导数,s为目标函数的输入参数
% tol为精度要求,verbose控制是否输出迭代过程
% x为输出最终解
% 参考文献:1)百度百科:牛顿迭代法
% 2)http://blog.sina.com.cn/s/blog_86186c970102vll8.html
% 3)http://www.maths.lth.se/na/courses/FMN081/FMN081-06/lecture8.pdf
if nargin < 6
verbose = 0;%默认不输出迭代过程
end
if nargin < 5
tol = 1e-3;
end
iter = 0;
x = x0;
if verbose
fprintf('Iter %d: x=%f,f(x)=%f\n',iter,x,Hxs(x,s,x0));
end
while abs(Hxs(x,s,x0)) > tol
x = x - Hxs(x,s,x0)/gx(x);%牛顿迭代公式
iter = iter + 1;
if verbose
fprintf('Iter %d: x=%f,f(x)=%f\n',iter,x,Hxs(x,s,x0));
end
end
end4)TestHomotopy.m(测试代码)
clear all;close all;clc;
x0 = 5;
s = 0:0.1:1;
x_star = zeros(length(s),1);
neginf = -20;posinf = 20;step = 0.05;
X_Plot = neginf:step:posinf;%作图横坐标
EnPlot = 1;%是否作图,1:是,0:否
if EnPlot
figure;plot(X_Plot,Hxs(X_Plot,s(1),x0),'r');%画出H(x,0),即F0(x)
xlabel('x');ylabel('H(x,s,x_0)');title('同伦函数曲线')
grid on;hold on;pause;
end
x_star(1) = x0;
for i=2:1:11
x_star(i) = NewtonIterHomo(x_star(i-1),@Hxs,@gx,s(i),1e-3,1);
if EnPlot
plot(X_Plot,Hxs(X_Plot,s(i),x_star(i)),'b');
hold on;pause;
end
end
if EnPlot
hold off;
end
figure;plot(s,x_star,'.-','MarkerEdgeColor','r','MarkerSize',20);grid;
xlabel('s');ylabel('x^*');title('同伦方法零点收敛过程');运行测试代码,可以发现最后的x迭代结果为x=0.000493,得到了正确的收敛的结果。
3、结束语
以前曾在文献中看到过同伦法,但也没有深究,近来在看SpaRSA算法时里面有个Continuation的概念,然后往上追踪到了FPC算法,在FPC的文献里又一次见到了Homotopymethod这个概念,看来是绕不过去了,那就花点时间吃掉它吧……
同伦法(homotopy method)有几个别名【2】:
注意括号里面的continuation method,那么continuation method翻译为中文应该是什么呢?查到的中文文献不多,在文献【5】的3.6节中将continuation翻译为“连续”,而在文献【6】中将continuation翻译为“持续”,有道词典是这样翻译的:
另外,发现有些老外的PPT做的很好,看起来很清晰,比如这次的文献【2】,这已经不是第一次受益于老外讲课的PPT了,同样一个概念,不同的讲法,但会产生截然不同的效果,能不能深入浅出的把一个复杂的概念讲明白是一项很重要的本事……
4、参考文献
【1】邓军. 基于凸优化的压缩感知信号恢复算法研究[D]. 哈尔滨工业大学, 2011.
【2】http://www.maths.lth.se/na/courses/FMN081/FMN081-06/lecture8.pdf
【3】百度百科,牛顿迭代法
【4】http://blog.csdn.net/itplus/article/details/21896453
【5】陈飞. 压缩感知凸优化方法分析[D].浙江大学, 2012.
【6】杨真真, 杨震.信号压缩与重构的交替方向外点持续法[J]. 电子学报,2014(3):485-490.









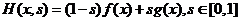
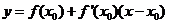
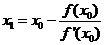
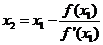
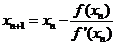
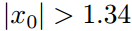


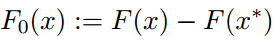
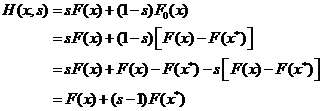















 328
328











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








