题目描述
给你一个序列X和另一个序列Z,当Z中的所有元素都在X中存在,并且在X中的下标顺序是严格递增的,那么就把Z叫做X的子序列。
例如:Z=<a,b,f,c>是序列X=<a,b,c,f,b,c>的一个子序列,Z中的元素在X中的下标序列为<1,2,4,6>。现给你两个序列X和Y,请问它们的最长公共子序列的长度是多少?
输入包含多组测试数据。每组输入占一行,为两个字符串,由若干个空格分隔。每个字符串的长度不超过100。
对于每组输入,输出两个字符串的最长公共子序列的长度。
abcfbc abfcab
programming contest
abcd mnp
样例输出
42
0
以字符串“sadstory”与“adminsorry”为例,其最长的公共子序列(为“adsory”,长度为6。
解题思路:令二维数组dp[i][j]表示字符串A的i号位和字符串B的j号位之前的最长公共子序列,如dp[4][6]表示“sads”和“admins”的最长公共子序列长度。那么A[i]和B[j]可以分为2种情况:
(1)A[i]==B[j],说明字符串A与 字符串B的最长公共子序列长度又增加了1位,即dp[i][j]=dp[i-1][j-1]+1。例如在样例中dp[4][6]表示示“sads”和“admins”,因为A[4]==B[6],所以dp[4][6]=dp[3][5]+1 即3
(2)A[i]!=B[j],说明字符串A的i号位和字符串B的j号位之前的最长公共子序列无法延长,因而dp[i][j]将会继承dp[i-1][j]和dp[i][j-1],即有dp[i][j]=max(dp[i-1][j],dp[i][j-1])。例如,dp[3][3]表示"sad"与“adm”的最长公共子序列的长度,但是A[3]!=B[3],这样dp[3][3]无法在原有的基础上延长,因此会继承“sa”与“adm”、“sad”与“ad”的最长公共子序列的较大值,即“sad”与“ad”的最长公共子序列长度2。(这里的i,j在某种意义上来说,地位是对等的)
由此可以得到状态转移方程:
边界:dp[i][0]=dp[0][j]=0 (字符串下标从1开始,下标0因此为0)
这样dp[i][j]就与之前的状态无关,由边界出发可以得到整个dp数组,最终dp[n][m]就是需要的结果,其实现代码如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int M=102;
int dp[M][M]; //默认边界为0
char str1[M],str2[M];
int main(){
int i,j;//从数组的下标1开始读取字符串
while(scanf("%s%s",str1+1,str2+1)!=EOF){
for(i=1;str1[i];i++){
for(j=1;str2[j];j++){
if(str1[i]==str2[j]){
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=max(dp[i][j-1],dp[i-1][j]);
}
}
}
printf("%d\n",dp[i-1][j-1]);//dp[i]为'\0'
}
}







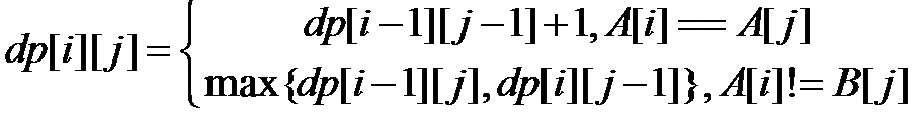














 1317
1317

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








