【排序算法】归并排序原理及Java实现

1、基本思想：

归并排序就是利用归并的思想实现的排序方法。而且充分利用了完全二叉树的深度是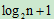的特性，因此效率比较高。其基本原理如下：对于给定的一组记录，利用递归与分治技术将数据序列划分成为越来越小的半子表，在对半子表排序，最后再用递归方法将排好序的半子表合并成为越来越大的有序序列。
经过第一轮比较后得到最小的记录，然后将该记录的位置与第一个记录的位置交换；接着对不包括第一个记录以外的其他记录进行第二次比较，得到最小记录并与第二个位置记录交换；重复该过程，知道进行比较的记录只剩下一个为止。

2、复杂度分析

一趟归并需要将数组 a[]中相邻的长度为h的有序序列进行两两归并.并将结果放到temp[]中，这需要将待排序列中的所有记录扫描一遍，因此耗费O(n)，而又完全二叉树的深度可知，整个归并排序需要进行（）次，因此总的时间复杂度为O(nlogn)，而且这是归并排序算法中最好、最坏、平均的时间性能。
由于归并排序在归并过程中需要与原始序列同样数量的存储空间存放归并结果以及递归时深度为的栈空间，因此空间复杂度为O(n+logn).
另外，对代码进行仔细研究，发现merge函数中有