codeforces round 400 E The Holmes Children 数学 欧拉函数

E. The Holmes Children

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The Holmes children are fighting over who amongst them is the cleverest.

Mycroft asked Sherlock and Eurus to find value of f(n), where f(1) = 1 and for n ≥ 2, f(n) is the number of distinct ordered positive integer pairs (x, y) that satisfy x + y = n and gcd(x, y) = 1. The integer gcd(a, b) is the greatest common divisor of a and b.

Sherlock said that solving this was child's play and asked Mycroft to instead get the value of 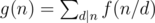. Summation is done over all positive integers d that divide n.

Eurus was quietly observing all this and finally came up with her problem to astonish both Sherlock and Mycroft.

She defined a k-composite function F_k(n) recursively as follows:

She wants them to tell the value of F_k(n) modulo 1000000007.

Input

A single line of input contains two space separated integers n (1 ≤ n ≤ 10¹²) and k (1 ≤ k ≤ 10¹²) indicating that Eurus asks Sherlock and Mycroft to find the value of F_k(n) modulo 1000000007.

Output

Output a single integer — the value of F_k(n) modulo 1000000007.

Examples

Input

7 1

Output

6

Input

10 2

Output

4

Note

In the first case, there are 6 distinct ordered pairs (1, 6), (2, 5), (3, 4), (4, 3), (5, 2) and (6, 1) satisfying x + y = 7 and gcd(x, y) = 1. Hence, f(7) = 6. So, F₁(7) = f(g(7)) = f(f(7) + f(1)) = f(6 + 1) = f(7) = 6.

题目描述：根据题目描述中的f、g、F函数，给定k、n，计算Fk(n)

思路:首先可以看出，f函数就是欧拉函数（不清楚的话可以先学一下），证明方式如下：

         对于数n，寻找满足gcd(a , n - a) = = 1的数a有多少个，因为gcd(a , n - a) == 1等价于gcd(a , n) == 1 (a < n)，那么就是统计满足gcd(a , n) == 1的a的数量，可以看到正是欧拉函数的定义。

        g函数满足g(x) = x，这个没有看出来怎么证明，但计算两个用例发现了这个规律

        所以，F函数就成了以下的形式

       F1(n) = f(g(n)) = f(n)

       F2(n) = g(F1(n)) = g(f(n)) = f(n)

       F3(n) = f(F2(n)) = f(f(n))

       F4(n) = g(F3(n)) = f(f(n))

       ...

       所以根据k的大小对n连续求欧拉函数就可以了，对一个数反复求欧拉函数，这个数下降非常快，一旦下降到1就结束了

收获：1、对于复杂的函数关系，先通过试的方式观察一下这个函数有没有什么特殊的性质

            2、对一个数连续求欧拉函数，这个数下降的速度非常快，虽然不会严格证明，可这是个既定的事实

#pragma warning(disable:4786)
#pragma comment(linker, "/STACK:102400000,102400000")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<vector>
#include<cmath>
#include<string>
#include<sstream>
#include<bitset>
#define LL long long
#define FOR(i,f_start,f_end) for(int i=f_start;i<=f_end;++i)
#define mem(a,x) memset(a,x,sizeof(a))
#define lson l,m,x<<1
#define rson m+1,r,x<<1|1
using namespace std;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
const double PI = acos(-1.0);
const double eps=1e-6;
const int maxn = 1e6 + 5;
int isprime[maxn],prime[maxn];
int pnum ;
void find_prime(int n)
{
    pnum = 0;
    mem(prime, 0);
    mem(isprime, 1);
    for(int i = 2 ; i < n ; i++){
        if(isprime[i])      prime[pnum++] = i;
        for(int j = 0; j<pnum && i * prime[j] < n ; j++){
            isprime[i * prime[j] ] = 0;
            if(i % prime[j] == 0)       break;
        }
    }
}
LL phi(LL n)
{
    LL ret = n;
    for(int i = 0 ; prime[i] * prime[i] <= n && i < pnum; i++){
        if(n % prime[i] == 0){
            ret = ret / prime[i] * (prime[i] - 1);
            while(n % prime[i] == 0){
                n /= prime[i];
            }
        }
    }
    if(n > 1)   ret = ret / n * (n - 1) ;
    return ret;
}
LL solve(LL time , LL n)
{
    LL last = n , cur = n;
    for(LL i = 1 ;i <= time;i ++){
        cur = phi(cur);
        if(cur == last)     return cur;
        last = cur;
    }
    return cur;
}
int main()
{
    LL k , n;
    scanf("%lld %lld" , &n , &k);
    find_prime(1e6 + 2);
    LL ans = solve((k + 1)/ 2 , n);
    printf("%lld\n",ans % mod);
    return 0;
}