霍夫曼编码实现

仅供日后参考，价值不定。

问题描述：

只考虑英文字母(不区分大小写)和空格，计算每个字符出现的频率，给出霍夫曼编码。

实现思路：

1.丛文件中读取文本，同时记录每个字符的频率，并初始化树

2.根据初始化的树建立霍夫曼树

3.根据霍夫曼树进行编码

4.输出

要编码的字符串：

FAST is an algorithm proposed originally by rosten and drummond for identifying interest points in an image.
An interest point in an image is a pixel which has a well defined position and can be robustly detected.
Interest points have high local information content and they should be ideally repeatable between different images.
Interest point detection has applications in image matching object recognition tracking etc.
Since establishing a match can be understood (THIS IS UPPER CASE) as classifying pairs of points as being a match or not.
A classifier that relies on these hamming distances will work best when their distributions are most separated.
As we will see in section this is of course what happens with recognition rates being higher in the first pairs of the wall sequence than in the subsequent ones.
We have introduced the brief descriptor that relies on a relatively small numberof intensity difference tests to represent an image patch as a binary string. Not only is construction and matching for this descriptor much faster than forother state of the art ones.
It also tends to yield higher recognition rates as long as invariance to large in plane rotations is not a requirement.

代码：

#include <stdio.h>
#include <ctype.h>
#include <stdlib.h>
int node_num = 0;//树的叶子节点数
int tree_array_len = 2 * node_num -1;//节点总数
#define MAX_CODE_LEN 100
/*霍夫曼树结构*/
typedef struct HuffTreeNode{
	int weight;//权重
	char c;
	int lchild,rchild,parent;
}HuffTree;
/*霍夫曼编码结构*/
typedef struct Code{
	char code[MAX_CODE_LEN];
	char ch;
	int start;
}HuffCode;
/*函数声明*/
void Read_Freq(char *filename,HuffTree *T);
void CreateHuffTree(HuffTree *T);
void CreateHuffCode(HuffTree *T,HuffCode *C);
void PrintCode_Single(HuffCode *C);

int main(){
	HuffTree *T;
	HuffCode *C;
	T = (HuffTree *)malloc(sizeof(HuffTreeNode)*100);
	printf("Frequence:\n");
	Read_Freq("E:\\test1.txt",T);
	C = (HuffCode *)malloc(sizeof(HuffCode)*node_num);
	CreateHuffTree(T);
	CreateHuffCode(T,C);
	printf("character encodings:\n");
	PrintCode_Single(C);
	free(T);
	free(C);
	return 0;
}
/*函数实现*/
void Read_Freq(char *filename,HuffTree *T){
	FILE *fp;
	if((fp = fopen(filename,"r"))==NULL){
		printf("Cannot Open File\n");
		exit(0);
	}
	char ch;
	int weight[28] = {0};//26个字母和一个空格
	ch = fgetc(fp);
	while(EOF != ch){
		if(isupper(ch)){
			ch += 32;
			ch -= 'a';
			weight[ch]++;
		}else if(islower(ch)){
			ch -= 'a';
			weight[ch]++;
		}else if(' '==ch){
			weight[26]++;
		}else{
			ch = fgetc(fp);
			continue;
		}
		ch = fgetc(fp);
	}
	/*读到树里去*/
	int k = 0;
	for(int i=0;i<26;i++){
		if(weight[i]>0){
			T[k].c = 'a' + i;
			T[k].weight = weight[i];
			T[k].lchild = T[k].rchild = -1;
			T[k].parent = 0;
			++k;
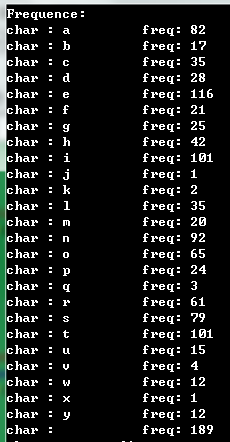
			printf("char : %c\t freq: %d\n",'a'+i,weight[i]);
			node_num ++;//记录字符的个数
		}
	}
	/*空格处理*/
	if(weight[26]>0){
	T[k].c = ' ';
	T[k].weight = weight[26];
	T[k].lchild = T[k].rchild = -1;
	T[k].parent = 0;
	k++;
	node_num ++;
	printf("char : %c\t freq: %d\n",' ',weight[26]);
	}
	fclose(fp);
}
void CreateHuffTree(HuffTree *T){
	int Max = 10000;//权值的最大可能值
	int i,j,p1,p2;//p1,p2指向s1,s2所指向的下标
	int s1,s2;//s1,s2指向权值最小的两个结点
	tree_array_len = 2 * node_num -1;
	for(i=node_num;i<tree_array_len;i++){
		T[i].parent = 0;
		T[i].lchild = T[i].rchild = -1;
		T[i].weight = 0;
	}
	for(i=node_num;i<tree_array_len;i++){
		p1=0;p2=0;
		s1=Max;s2=Max;   
		for(j=0;j<i;j++){   //选出两个权值最小的根结点
			if(T[j].parent==0){
				if(T[j].weight<s1)
				{
					s2=s1;  //改变最小权、次小权及对应的位置
					s1=T[j].weight;
					p2=p1;
					p1=j;
				}
				else{
					if(T[j].weight<s2)
					{
						s2=T[j].weight;  //改变次小权及位置
						p2=j;
					}
				}
			}
		}
		T[p1].parent=i;
		T[p2].parent=i;
		T[i].lchild=p1;  //最小权根结点是新结点的左孩子
		T[i].rchild=p2;  //次小权根结点是新结点的右孩子
		T[i].weight=T[p1].weight+T[p2].weight;
	}
}
void CreateHuffCode(HuffTree *T,HuffCode *C){
	int i,c,p;
	HuffCode code;   
	for(i=0;i<node_num;i++)
	{
		code.start=node_num;
		code.ch=T[i].c;
		c=i;       //从叶结点出发向上回溯
		p=T[i].parent;   //p是T[i]的双亲
		while(p!=0)//没到根节点
		{
			code.start--;
			if(T[p].lchild==c){
				code.code[code.start]='0';   //T[i]是左子树，代码'0'
			}else{
				code.code[code.start]='1';   //T[i]是右子树，代码'1'
			}
			c=p;
			p=T[p].parent;
		}
		C[i]=code;    //编码存入C[i]
	}
}
void PrintCode_Single(HuffCode *C){
	for(int i=0;i<node_num;i++){
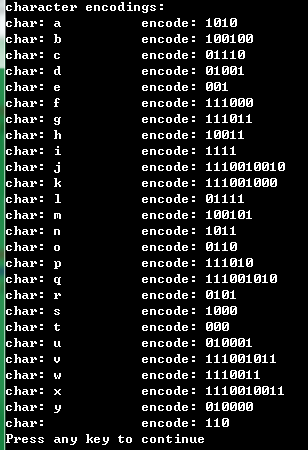
		printf("char: %c\t\t encode: ",C[i].ch);
		for(int j=C[i].start;j<node_num;j++){
			printf("%c",C[i].code[j]);
		}
		printf("\n");
	}
}
void GetCode(char ch,HuffCode *C,int &count){
	count = 0;
	for(int i=0;i<node_num;i++){
		if(ch==C[i].ch){
			for(int j=C[i].start;j<node_num;j++){
				printf("%c",C[i].code[j]);
				count++;
			}
			return ;
		}
	}
}

运行结果：

频率 编码：