在数值分析中,多项式插值用多项式对一组给定的数据进行插值。本文将从拉格朗日插值
讲到牛顿均差插值、切比雪夫插值。
一、拉格朗日插值
1.1、什么是拉格朗日插值?
假设有n个数据点 (x1, y1),...,(xn,yn) ,对于每一个1<=k<=n,定义 (n-1)阶多项式
则定义 n-1阶多项式
这个多项式就是拉格朗日插值多项式。而给定n个数据点,求出一个n-1阶(准确地说,不超过n-1阶)
多项式,使得这个多项式对应的函数经过这n个数据点的过程就叫拉格朗日插值。
将任何一个数据点(xk,yk)(1<=k<=n)带入到拉格朗日多项式Pn-1(x)中,很明显Pn-1(xk)=0。
举个例子,对于三个数据点(0,1), (2, 2), (3, 4), 对应的拉格朗日插值多项式为
即 2阶函数 f(x)=经过点(0, 1), (2, 2), (3, 4), 也就是f(x)插值这三个点。
这里需要注意的是,对于n个数据点,对应的拉格朗日插值多项式不一定是n-1阶,可能小于n-1阶。
例如,经过点(0, 2), (1, 1), (2, 0) 的拉格朗日插值多项式是 P(x) = -x + 2 ,是一阶的。
二、牛顿均差插值
2.1 牛顿均差插值介绍
正如上面所示,拉格朗日插值法能够很方便写出经过n个点的插值多项式。但是在实际中,
拉格朗日插值法很少用于计算,因为有多种可供选择的更加便于管理和计算复杂度更低的形式。
牛顿均差插值法就是其中一种。
给定n个点,定义n-1阶多项式
这个多项式就是牛顿均值插值多项式。
其中, 各项的系数可以有下面对应公式计算得到
其它各项系数,以此类推。
上面计算各项系数的公式有点不好理解,说白了,可以将所有的系数存放在一个二维数组a里,
其中系数从x的0次项到x的(n-1)次项的系数依次等于a[0][0], a[1][1], ...., a[n-1][n-1]。
对于j=0, a[i][j]=f(xi)(0<=i<n); 当i>=1且j>=1时, a[i][j] = (a[i][j-1] - a[i-1][j-1]) / (x(i) - x(i-j)) ;
这样可能还是有点抽象,下面举个例子来加深理解。
对于点(0, 1), (2, 2), (3, 4), 多项式各项系数对应的二维数组a,
a[0][0] = f(x0) = f(0) = 1,
a[1][0] = f(x1) = f(2) = 2, a[1][1] = (a[1][0] - a[0][0]) / (x1 - x(1-0)) = (2-1)/(2-0) = 1/2;
a[2][0] = f(x2) = f(3) = 4, a[2][1] = (a[2][0] - a[1][0]) / (x2 - x(2-1)) = (4-2)/(3-2) = 2,
a[2][2] = (a[2][1] - a[1][1]) / (x2 - x(2-2)) = (2-1/2) / (3-0) = 1/2;
则经过这三个点的牛顿均差插值多项式是
P(x) = 1 + (x-0)/2 + (x-0)(x-2)/2
由上面的叙述,我们很容易就能用程序实现牛顿均差插值。
2.2 牛顿均差插值程序实现
牛顿均差插值程序实现主要代码如下:
public class NewtonMean {
private double[][] points; //points to get theirs Newton Interpolation
public NewtonMean(double[][] points) {
this.points = points;
}
/* Get Newton Interpolation of points given */
public double[] newtonMean() {
if(points[0].length != 2) {
throw new IllegalArgumentException("Each row of points can only " +
"have two elements, the first for x, the other for y.");
}
return computeCoefficients();
}
/* Compute coefficient for each item of Polynomial */
private double[] computeCoefficients() {
/* Compute mean difference */
double[][] meanDifference = new double[points.length][points.length];
for(int i=0; i<meanDifference.length; i++) {
meanDifference[i][0] = points[i][1];
}
for(int i=0; i<meanDifference.length; i++) {
for(int j=1; j<=i; j++) {
meanDifference[i][j] = (meanDifference[i][j-1] - meanDifference[i-1][j-1]) /
(points[i][0] - points[i-j][0]);
}
}
/* Get coefficient of each item */
double[] coefficients = new double[points.length];
for(int i=0; i<coefficients.length; i++) {
coefficients[i] = meanDifference[i][i];
}
return coefficients;
}
}牛顿均差插值法相对拉格朗日插值法另一个优点是,增加一个节点时,牛顿均差插值法只需在当前得到的
插值多项式的基础上添加一项即可,而Lagrange 插值所有的基函数都需要重新计算。
三、切比雪夫插值
切比雪夫插值的提出是为了改善插值在差值区间上的最大误差控制
3.1 切比雪夫插值节点的选取
对于一个插值区间 [a, b], 如果要在这个插值区间上选取n个点作为插值基点,使得上面的最大误差
最小,则基点的选法如下:
对于 i = 1, 2, ...., n. 下面的不等式在区间 [a, b] 上满足
3.2 切比雪夫插值程序实现
上面已经实现了牛顿均差插值,切比雪夫插值只要在插值区间上选取出插值基点后,再调用
牛顿均值差值法即可实现。
其代码实现如下(以函数 f(x)=sinx 的插值为例):
public class ChebyshevInterpolation {
private double rangeStart; //Start value of range
private double rangeEnd; //End value of range
private int numberOfBasicPoints;
public ChebyshevInterpolation(double rangeStart, double rangeEnd,
int numberOfBasicPoints) {
this.rangeStart = rangeStart;
this.rangeEnd = rangeEnd;
this.numberOfBasicPoints = numberOfBasicPoints;
}
/* Chebyshev Interpolation */
public double[] chebyshevInterpolation() {
double[][] generatedBasicPoints = generateBasicPoints();
NewtonMean newton = new NewtonMean(generatedBasicPoints);
return newton.newtonMean();
}
/* Generate basic points */
private double[][] generateBasicPoints() {
double[][] points = new double[numberOfBasicPoints][2];
double scaling = (rangeEnd - rangeStart)/2;
double displacement = (rangeStart + rangeEnd)/2;
double factor = Math.PI/(2*numberOfBasicPoints);
for(int i=0; i<points.length; i++) {
points[i][0] = scaling * Math.cos((2*i + 1)*factor) + displacement ;
points[i][1] = func(points[i][0]);
}
return points;
}
/* Get function value of x */
private double func(double x) {
return Math.sin(x);
}
}








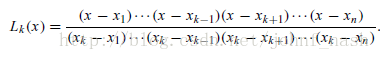
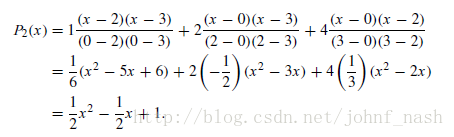
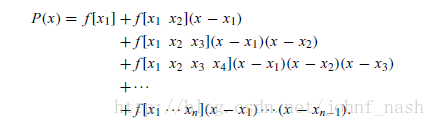
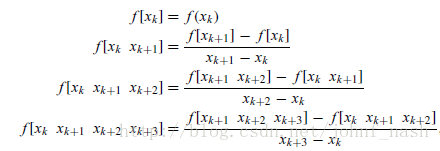
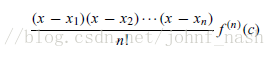
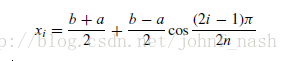
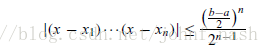

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








