SVM
- 线性可分支持向量机:数据线性可分时,硬间隔最大化,又称硬间隔SVM
- 线性支持向量机 :数据近似线性可分时,软间隔最大化,又称软间隔SVM
- 非线性支持向量机 :数据线性不可分时,核技巧,转化为软间隔SVM
线性SVM:假设输入空间与特征空间的元素直接一 一对应,将输入空间的输入映射为特征空间中的特征向量。
非线性SVM:利用一个从输入空间到特征空间的非线性映射,来将输入映射为特征向量。
所以输入都由输入空间转换到特征空间,SVM的学习在特征空间中进行。
- 感知机:误分类个数最小的策略,求分离超平面(解无穷多);感知机训练时,误分类个数最小即可(转化为值大于0),衡量上较粗略。
- SVM:间隔最大化,求泛化能力最强的那个超平面(解唯一);SVM使用距离,将误分类误差细化(值大于1)。
不同分离超平面,误分类个数可能是相同的,但误分类距离绝对不同。
有关svm的内容实在太多了,具体可以看李航的《统计学习方法》这本书。
线性可分SVM
对于二类分类问题,训练集T={(x1,y1),(x2,y2),⋯,(xN,yN)},其类别yi∈{0,1},线性SVM通过学习得到分离超平面
w⋅x+b=0*注解:w为法向量,决定了超平面的方向;b为位移项,决定了超平面与原点之间的距离样本空间中,任意点 x到超平面的距离为
得到相应的分类决策函数:
f(x)=sign(w⋅x+b)
如图所示:
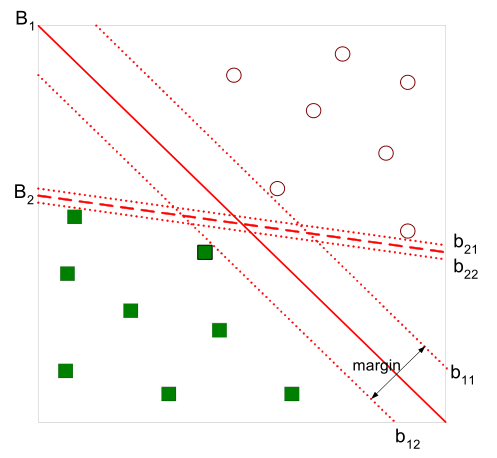
直观上,超平面B1的分类效果更好一些。该超平面对训练样本局部扰动的容忍性最好,将距离分离超平面最近的两个不同类别的样本点称为支持向量的,构成了两条平行于分离超平面的长带,二者之间的距离称之为margin。显然,margin更大,则分类正确的确信度更高(与超平面的距离表示分类的确信度,距离越远则分类正确的确信度越高)。
通过计算得到:
SVM是有很重要的训练样本(支持向量)所确定的。至此,SVM分类问题可描述为在全部分类正确的情况下,最大化margin;
线性分类的约束最优化问题:
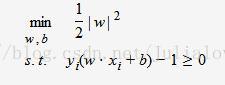
对每一个不等式约束引进拉格朗日乘子αi≥0,i=1,2,⋯,N;
构造拉格朗日函数:
根据拉格朗日对偶性,原始的约束最优化问题可等价于极大极小的对偶问题:
将L(w,b,α)对w,b求偏导并令其等于0,则
将上述式子代入拉格朗日函数中,对偶问题转为
等价于最优化问题:
线性可分是理想情形,大多数情况下,由于噪声或特异点等各种原因,训练样本是线性不可分的。
线性不可分SVM
线性不可分意味着有样本点不满足约束条件,为了解决这个问题,对每个样本引入一个松弛变量ξi≥0,这样约束条件变为:
yi(w⋅xi+b)≥1−ξi
目标函数则变为
其中,C为惩罚函数,目标函数有两层含义:
- margin尽量大,
- 误分类的样本点计量少
C为调节二者的参数。通过构造拉格朗日函数并求解偏导(具体推导略去),可得到等价的对偶问题:
与上一节中线性可分的对偶问题相比,只是约束条件αi发生变化,问题求解思路与之类似。
非线性SVM
通过空间变换ϕ(一般是低维空间映射到高维空间x→ϕ(x))后实现线性可分,在下图所示的例子中,通过空间变换,将左图中的椭圆分离面变换成了右图中直线。
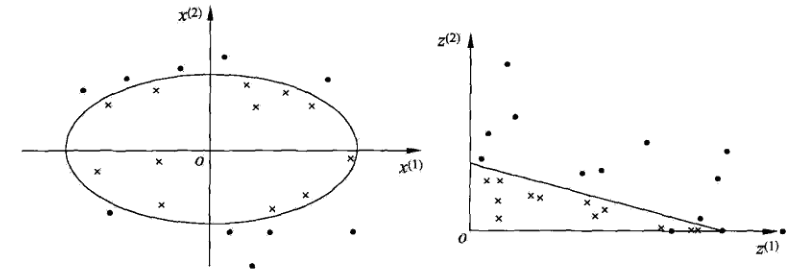
在SVM的等价对偶问题中的目标函数中有样本点的内积xi⋅xj,在空间变换后则是ϕ(xi)⋅ϕ(xj),由于维数增加导致内积计算成本增加,然后核函数(kernel function)将映射后的高维空间内积转换成低维空间的函数:
K(x,z)=ϕ(x)⋅ϕ(z)
将其代入一般化的SVM学习算法的目标函数中,可得非线性SVM的最优化问题:
核函数:
核技巧:使得SVM成为实质上的非线性分类器。
输入为欧式空间(如常用的二维平面,三维立体空间)或离散空间时,特征空间为希尔伯特空间(向量是其中元素)时,核函数表示将输入从输入空间映射到特征空间得到的特征向量之间的内积。
对偶形式中恰好求解向量间内积,直接替换即可。核函数的巧妙之处,不需要显示知道映射函数,只需要内积。
用核函数可学习非线性SVM,等价于隐式地在高维特征空间中学习线性SVM。这样的方法称为核技巧(kernel trick)。核方法是比SVM更为一般的ML方法。SVM可看作是核函数为 x->x映射的核技巧。
线性核函数:
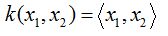
★多项式核函数:
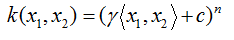
★径像基核函数/高斯核函数:

★拉普拉斯核函数:

★sigmod核函数:
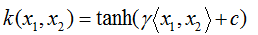
对偶问题

凸优化问题

KTT条件

代码练习:
1、Sclearn中的案例:http://scikit-learn.org/stable/auto_examples/index.html#support-vector-machines
2、鸢尾花分类:iris.data
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2018/6/21 8:33
# @Author : Julia
# @Site :
# @File : SVM.py
# @Software: PyCharm
from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from matplotlib import colors
from sklearn.cross_validation import train_test_split
# 将第五列转为folat类型
def iris_type(s):
it = {'Iris-setosa': 0, 'Iris-versicolor': 1, 'Iris-virginica': 2}
return it[s]
def show_accuracy(y_hat, y_test, param):
pass
path = 'iris.data'
# loadtxt(path路径,dtype数据类型,delimiter分隔符,converters将数据列和转换函数进行映射的字典,选取数据的列,usecols:选取数据的列)
data = np.loadtxt(path, dtype=float, delimiter=',', converters={4: iris_type})
x, y = np.split(data, (4,), axis=1) # 数据,分割位置,轴=1:水平,0垂直分割
x = x[:, :2] # 为方便后期画图,支取前两列特征值向量训练
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1, train_size=0.6)
'''
kernel='linear'时,为线性核,C越大分类效果越好,但有可能会过拟合(defaul C=1)。
kernel='rbf'时(default),为高斯核,gamma值越小,分类界面越连续;gamma值越大,分类界面越“散”,分类效果越好,但有可能会过拟合。
decision_function_shape='ovr'时,为one v rest,即一个类别与其他类别进行划分,
decision_function_shape='ovo'时,为one v one,即将类别两两之间进行划分,用二分类的方法模拟多分类的结果。
'''
# 训练
# clf = svm.SVC(C=0.1, kernel='linear', decision_function_shape='ovr')
clf = svm.SVC(C=0.8, kernel='rbf', gamma=20, decision_function_shape='ovr')
clf.fit(x_train, y_train.ravel())
# 测试
print '训练集精度:', clf.score(x_train, y_train) # 精度
y_hat = clf.predict(x_train)
show_accuracy(y_hat, y_train, '训练集')
print '测试集精度', clf.score(x_test, y_test)
y_hat = clf.predict(x_test)
show_accuracy(y_hat, y_test, '测试集')
print 'decision_function:\n', clf.decision_function(x_train)
# decision_function中每一列的值代表距离各类别的距离。
print '\npredict:\n', clf.predict(x_train)
# 绘制图像
x1_min, x1_max = x[:, 0].min(), x[:, 0].max() # 第0列的范围
x2_min, x2_max = x[:, 1].min(), x[:, 1].max() # 第1列的范围
x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j] # 生成网格采样点
grid_test = np.stack((x1.flat, x2.flat), axis=1) # 测试点
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
# print 'grid_test = \n', grid_test
grid_hat = clf.predict(grid_test) # 预测分类值
grid_hat = grid_hat.reshape(x1.shape) # 使之与输入的形状相同
alpha = 0.5
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light) # 预测值的显示
# plt.scatter(x[:, 0], x[:, 1], c=y, edgecolors='k', s=50, cmap=cm_dark) # 样本
plt.plot(x[:, 0], x[:, 1], 'o', alpha=alpha, color='blue', markeredgecolor='k')
plt.scatter(x_test[:, 0], x_test[:, 1], s=120, facecolors='none', zorder=10) # 圈中为测试集样本
plt.xlabel(u'花萼长度', fontsize=13)
plt.ylabel(u'花萼宽度', fontsize=13)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.title(u'鸢尾花SVM二特征分类', fontsize=20)
plt.grid()
plt.show()
3、后台实现1:dataset
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2018/6/21 10:04
# @Author : Julia
# @Site :
# @File : SVM_b.py
# @Software: PyCharm
from numpy import *
def loadDataSet(filename): #读取数据
dataMat=[]
labelMat=[]
fr=open(filename)
for line in fr.readlines():
lineArr=line.strip().split('\t')
dataMat.append([float(lineArr[0]),float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat #返回数据特征和数据类别
def selectJrand(i,m): #在0-m中随机选择一个不是i的整数
j=i
while (j==i):
j=int(random.uniform(0,m))
return j
def clipAlpha(aj,H,L): #保证a在L和H范围内(L <= a <= H)
if aj>H:
aj=H
if L>aj:
aj=L
return aj
def kernelTrans(X, A, kTup): #核函数,输入参数,X:支持向量的特征树;A:某一行特征数据;kTup:('lin',k1)核函数的类型和参数
m,n = shape(X)
K = mat(zeros((m,1)))
if kTup[0]=='lin': #线性函数
K = X * A.T
elif kTup[0]=='rbf': # 径向基函数(radial bias function)
for j in range(m):
deltaRow = X[j,:] - A
K[j] = deltaRow*deltaRow.T
K = exp(K/(-1*kTup[1]**2)) #返回生成的结果
else:
raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
return K
#定义类,方便存储数据
class optStruct:
def __init__(self,dataMatIn, classLabels, C, toler, kTup): # 存储各类参数
self.X = dataMatIn #数据特征
self.labelMat = classLabels #数据类别
self.C = C #软间隔参数C,参数越大,非线性拟合能力越强
self.tol = toler #停止阀值
self.m = shape(dataMatIn)[0] #数据行数
self.alphas = mat(zeros((self.m,1)))
self.b = 0 #初始设为0
self.eCache = mat(zeros((self.m,2))) #缓存
self.K = mat(zeros((self.m,self.m))) #核函数的计算结果
for i in range(self.m):
self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)
def calcEk(oS, k): #计算Ek(参考《统计学习方法》p127公式7.105)
fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
#随机选取aj,并返回其E值
def selectJ(i, oS, Ei):
maxK = -1
maxDeltaE = 0
Ej = 0
oS.eCache[i] = [1,Ei]
validEcacheList = nonzero(oS.eCache[:,0].A)[0] #返回矩阵中的非零位置的行数
if (len(validEcacheList)) > 1:
for k in validEcacheList:
if k == i:
continue
Ek = calcEk(oS, k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE): #返回步长最大的aj
maxK = k
maxDeltaE = deltaE
Ej = Ek
return maxK, Ej
else:
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
def updateEk(oS, k): #更新os数据
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]
#首先检验ai是否满足KKT条件,如果不满足,随机选择aj进行优化,更新ai,aj,b值
def innerL(i, oS): #输入参数i和所有参数数据
Ei = calcEk(oS, i) #计算E值
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)): #检验这行数据是否符合KKT条件 参考《统计学习方法》p128公式7.111-113
j,Ej = selectJ(i, oS, Ei) #随机选取aj,并返回其E值
alphaIold = oS.alphas[i].copy()
alphaJold = oS.alphas[j].copy()
if (oS.labelMat[i] != oS.labelMat[j]): #以下代码的公式参考《统计学习方法》p126
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H:
print("L==H")
return 0
eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #参考《统计学习方法》p127公式7.107
if eta >= 0:
print("eta>=0")
return 0
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta #参考《统计学习方法》p127公式7.106
oS.alphas[j] = clipAlpha(oS.alphas[j],H,L) #参考《统计学习方法》p127公式7.108
updateEk(oS, j)
if (abs(oS.alphas[j] - alphaJold) < oS.tol): #alpha变化大小阀值(自己设定)
print("j not moving enough")
return 0
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#参考《统计学习方法》p127公式7.109
updateEk(oS, i) #更新数据
#以下求解b的过程,参考《统计学习方法》p129公式7.114-7.116
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
if (0 < oS.alphas[i]<oS.C):
oS.b = b1
elif (0 < oS.alphas[j]<oS.C):
oS.b = b2
else:
oS.b = (b1 + b2)/2.0
return 1
else:
return 0
#SMO函数,用于快速求解出alpha
def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)): #输入参数:数据特征,数据类别,参数C,阀值toler,最大迭代次数,核函数(默认线性核)
oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
iter = 0
entireSet = True
alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet:
for i in range(oS.m): #遍历所有数据
alphaPairsChanged += innerL(i,oS)
print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged)) #显示第多少次迭代,那行特征数据使alpha发生了改变,这次改变了多少次alpha
iter += 1
else:
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs: #遍历非边界的数据
alphaPairsChanged += innerL(i,oS)
print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
iter += 1
if entireSet:
entireSet = False
elif (alphaPairsChanged == 0):
entireSet = True
print("iteration number: %d" % iter)
return oS.b,oS.alphas
def testRbf(data_train,data_test):
dataArr,labelArr = loadDataSet(data_train) #读取训练数据
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', 1.3)) #通过SMO算法得到b和alpha
datMat=mat(dataArr)
labelMat = mat(labelArr).transpose()
svInd=nonzero(alphas)[0] #选取不为0数据的行数(也就是支持向量)
sVs=datMat[svInd] #支持向量的特征数据
labelSV = labelMat[svInd] #支持向量的类别(1或-1)
print("there are %d Support Vectors" % shape(sVs)[0]) #打印出共有多少的支持向量
m,n = shape(datMat) #训练数据的行列数
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', 1.3)) #将支持向量转化为核函数
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b #这一行的预测结果(代码来源于《统计学习方法》p133里面最后用于预测的公式)注意最后确定的分离平面只有那些支持向量决定。
if sign(predict)!=sign(labelArr[i]): #sign函数 -1 if x < 0, 0 if x==0, 1 if x > 0
errorCount += 1
print("the training error rate is: %f" % (float(errorCount)/m)) #打印出错误率
dataArr_test,labelArr_test = loadDataSet(data_test) #读取测试数据
errorCount_test = 0
datMat_test=mat(dataArr_test)
labelMat = mat(labelArr_test).transpose()
m,n = shape(datMat_test)
for i in range(m): #在测试数据上检验错误率
kernelEval = kernelTrans(sVs,datMat_test[i,:],('rbf', 1.3))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr_test[i]):
errorCount_test += 1
print("the test error rate is: %f" % (float(errorCount_test)/m))
#主程序
def main():
filename_traindata='train_data'
filename_testdata='test_data'
testRbf(filename_traindata,filename_testdata)
if __name__=='__main__':
main()4、后台实现2:
cvxopt: https://uqer.io/v3/community/share/55c9a55df9f06c91f818c675
# -*- coding: utf-8 -*-
"""
Created on Tue Nov 22 11:24:22 2017
@author: Julia
"""
import numpy as np
from numpy import linalg
import cvxopt
import cvxopt.solvers
def linear_kernel(x1, x2):
return np.dot(x1, x2)
def polynomial_kernel(x, y, p=3):
return (1 + np.dot(x, y)) ** p
def gaussian_kernel(x, y, sigma=5.0):
return np.exp(-linalg.norm(x-y)**2 / (2 * (sigma ** 2)))
class SVM(object):
def __init__(self, kernel=linear_kernel, C=None):
self.kernel = kernel
self.C = C
if self.C is not None: self.C = float(self.C)
def fit(self, X, y):
n_samples, n_features = X.shape
# Gram matrix
K = np.zeros((n_samples, n_samples))
for i in range(n_samples):
for j in range(n_samples):
K[i,j] = self.kernel(X[i], X[j])
P = cvxopt.matrix(np.outer(y,y) * K)
q = cvxopt.matrix(np.ones(n_samples) * -1)
A = cvxopt.matrix(y, (1,n_samples))
b = cvxopt.matrix(0.0)
if self.C is None:
G = cvxopt.matrix(np.diag(np.ones(n_samples) * -1))
h = cvxopt.matrix(np.zeros(n_samples))
else:
tmp1 = np.diag(np.ones(n_samples) * -1)
tmp2 = np.identity(n_samples)
G = cvxopt.matrix(np.vstack((tmp1, tmp2)))
tmp1 = np.zeros(n_samples)
tmp2 = np.ones(n_samples) * self.C
h = cvxopt.matrix(np.hstack((tmp1, tmp2)))
# solve QP problem
solution = cvxopt.solvers.qp(P, q, G, h, A, b)
# Lagrange multipliers
'''
数组的flatten和ravel方法将数组变为一个一维向量(铺平数组)。
flatten方法总是返回一个拷贝后的副本,
而ravel方法只有当有必要时才返回一个拷贝后的副本(所以该方法要快得多,尤其是在大数组上进行操作时)
'''
a = np.ravel(solution['x'])
# Support vectors have non zero lagrange multipliers
'''
这里a>1e-5就将其视为非零
'''
sv = a > 1e-5 # return a list with bool values
ind = np.arange(len(a))[sv] # sv's index
self.a = a[sv]
self.sv = X[sv] # sv's data
self.sv_y = y[sv] # sv's labels
print("%d support vectors out of %d points" % (len(self.a), n_samples))
# Intercept
'''
这里相当于对所有的支持向量求得的b取平均值
'''
self.b = 0
for n in range(len(self.a)):
self.b += self.sv_y[n]
self.b -= np.sum(self.a * self.sv_y * K[ind[n],sv])
self.b /= len(self.a)
# Weight vector
if self.kernel == linear_kernel:
self.w = np.zeros(n_features)
for n in range(len(self.a)):
# linear_kernel相当于在原空间,故计算w不用映射到feature space
self.w += self.a[n] * self.sv_y[n] * self.sv[n]
else:
self.w = None
def project(self, X):
# w有值,即kernel function 是 linear_kernel,直接计算即可
if self.w is not None:
return np.dot(X, self.w) + self.b
# w is None --> 不是linear_kernel,w要重新计算
# 这里没有去计算新的w(非线性情况不用计算w),直接用kernel matrix计算预测结果
else:
y_predict = np.zeros(len(X))
for i in range(len(X)):
s = 0
for a, sv_y, sv in zip(self.a, self.sv_y, self.sv):
s += a * sv_y * self.kernel(X[i], sv)
y_predict[i] = s
return y_predict + self.b
def predict(self, X):
return np.sign(self.project(X))
if __name__ == "__main__":
import pylab as pl
def gen_lin_separable_data():
# generate training data in the 2-d case
mean1 = np.array([0, 2])
mean2 = np.array([2, 0])
cov = np.array([[0.8, 0.6], [0.6, 0.8]])
X1 = np.random.multivariate_normal(mean1, cov, 100)
y1 = np.ones(len(X1))
X2 = np.random.multivariate_normal(mean2, cov, 100)
y2 = np.ones(len(X2)) * -1
return X1, y1, X2, y2
def gen_non_lin_separable_data():
mean1 = [-1, 2]
mean2 = [1, -1]
mean3 = [4, -4]
mean4 = [-4, 4]
cov = [[1.0,0.8], [0.8, 1.0]]
X1 = np.random.multivariate_normal(mean1, cov, 50)
X1 = np.vstack((X1, np.random.multivariate_normal(mean3, cov, 50)))
y1 = np.ones(len(X1))
X2 = np.random.multivariate_normal(mean2, cov, 50)
X2 = np.vstack((X2, np.random.multivariate_normal(mean4, cov, 50)))
y2 = np.ones(len(X2)) * -1
return X1, y1, X2, y2
def gen_lin_separable_overlap_data():
# generate training data in the 2-d case
mean1 = np.array([0, 2])
mean2 = np.array([2, 0])
cov = np.array([[1.5, 1.0], [1.0, 1.5]])
X1 = np.random.multivariate_normal(mean1, cov, 100)
y1 = np.ones(len(X1))
X2 = np.random.multivariate_normal(mean2, cov, 100)
y2 = np.ones(len(X2)) * -1
return X1, y1, X2, y2
def split_train(X1, y1, X2, y2):
X1_train = X1[:90]
y1_train = y1[:90]
X2_train = X2[:90]
y2_train = y2[:90]
X_train = np.vstack((X1_train, X2_train))
y_train = np.hstack((y1_train, y2_train))
return X_train, y_train
def split_test(X1, y1, X2, y2):
X1_test = X1[90:]
y1_test = y1[90:]
X2_test = X2[90:]
y2_test = y2[90:]
X_test = np.vstack((X1_test, X2_test))
y_test = np.hstack((y1_test, y2_test))
return X_test, y_test
# 仅仅在Linears使用此函数作图,即w存在时
def plot_margin(X1_train, X2_train, clf):
def f(x, w, b, c=0):
# given x, return y such that [x,y] in on the line
# w.x + b = c
return (-w[0] * x - b + c) / w[1]
pl.plot(X1_train[:,0], X1_train[:,1], "ro")
pl.plot(X2_train[:,0], X2_train[:,1], "bo")
pl.scatter(clf.sv[:,0], clf.sv[:,1], s=100, c="g")
# w.x + b = 0
a0 = -4; a1 = f(a0, clf.w, clf.b)
b0 = 4; b1 = f(b0, clf.w, clf.b)
pl.plot([a0,b0], [a1,b1], "k")
# w.x + b = 1
a0 = -4; a1 = f(a0, clf.w, clf.b, 1)
b0 = 4; b1 = f(b0, clf.w, clf.b, 1)
pl.plot([a0,b0], [a1,b1], "k--")
# w.x + b = -1
a0 = -4; a1 = f(a0, clf.w, clf.b, -1)
b0 = 4; b1 = f(b0, clf.w, clf.b, -1)
pl.plot([a0,b0], [a1,b1], "k--")
pl.axis("tight")
pl.show()
def plot_contour(X1_train, X2_train, clf):
# 作training sample数据点的图
pl.plot(X1_train[:,0], X1_train[:,1], "ro")
pl.plot(X2_train[:,0], X2_train[:,1], "bo")
# 做support vectors 的图
pl.scatter(clf.sv[:,0], clf.sv[:,1], s=100, c="g")
X1, X2 = np.meshgrid(np.linspace(-6,6,50), np.linspace(-6,6,50))
X = np.array([[x1, x2] for x1, x2 in zip(np.ravel(X1), np.ravel(X2))])
Z = clf.project(X).reshape(X1.shape)
# pl.contour做等值线图
pl.contour(X1, X2, Z, [0.0], colors='k', linewidths=1, origin='lower')
pl.contour(X1, X2, Z + 1, [0.0], colors='grey', linewidths=1, origin='lower')
pl.contour(X1, X2, Z - 1, [0.0], colors='grey', linewidths=1, origin='lower')
pl.axis("tight")
pl.show()
def test_linear():
X1, y1, X2, y2 = gen_lin_separable_data()
X_train, y_train = split_train(X1, y1, X2, y2)
X_test, y_test = split_test(X1, y1, X2, y2)
clf = SVM()
clf.fit(X_train, y_train)
y_predict = clf.predict(X_test)
correct = np.sum(y_predict == y_test)
print("%d out of %d predictions correct" % (correct, len(y_predict)))
plot_margin(X_train[y_train==1], X_train[y_train==-1], clf)
def test_non_linear():
X1, y1, X2, y2 = gen_non_lin_separable_data()
X_train, y_train = split_train(X1, y1, X2, y2)
X_test, y_test = split_test(X1, y1, X2, y2)
clf = SVM(gaussian_kernel)
clf.fit(X_train, y_train)
y_predict = clf.predict(X_test)
correct = np.sum(y_predict == y_test)
print("%d out of %d predictions correct" % (correct, len(y_predict)))
plot_contour(X_train[y_train==1], X_train[y_train==-1], clf)
def test_soft():
X1, y1, X2, y2 = gen_lin_separable_overlap_data()
X_train, y_train = split_train(X1, y1, X2, y2)
X_test, y_test = split_test(X1, y1, X2, y2)
clf = SVM(C=0.1)
clf.fit(X_train, y_train)
y_predict = clf.predict(X_test)
correct = np.sum(y_predict == y_test)
print("%d out of %d predictions correct" % (correct, len(y_predict)))
plot_contour(X_train[y_train==1], X_train[y_train==-1], clf)
# test_soft()
# test_linear()
test_non_linear()









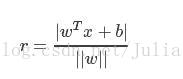
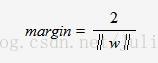
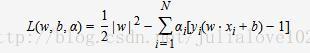
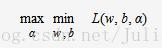
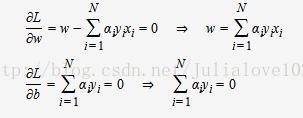
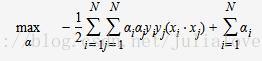
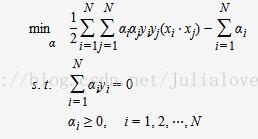
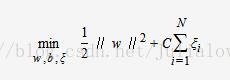
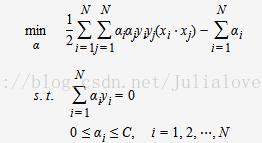
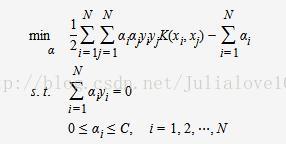














 1531
1531











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










