首先给出这个Lucas定理:
A、B是非负整数,p是质数。AB写成p进制:A=a[n]a[n-1]...a[0],B=b[n]b[n-1]...b[0]。
则组合数C(A,B)与C(a[n],b[n])*C(a[n-1],b[n-1])*...*C(a[0],b[0]) modp同余
即:Lucas(n,m,p)=c(n%p,m%p)*Lucas(n/p,m/p,p)
For non-negative integers m and n and a prime p, the following congruence relationholds:
-
 表示的是同余,表示两个数对p取余,余数相同。
表示的是同余,表示两个数对p取余,余数相同。
where
and
are the base p expansions of m and n respectively.
证明:
http://en.wikipedia.org/wiki/Lucas%27_theorem
维基的意思是说在m中里面取n个%p来说,这样考虑:
将m划分成m0个1,m1个p,m2个p^2,……
将n划分成n0个1,n1个p,n2个p^2……
那是不是C(m,n)的总共的取法就是( 在m0个里面取n0个的方案数 * m1个里面取n1个的方案数 * m2个里面取n2个的方案数 ……)
证明就是这样。
之所以看lucas,是因为12年多校有Lucas定理的题。
咳咳,我们先来看看hdu3037.
意思是说将不少于m个球放在n个盒子里面。
做ACM做多了,把高中知识都忘了-------其实就是将m + n个球放在n个盒子当中有多少放法,就用Lucas来做呗。
其中,由于涉及到还有取模,需要运用求乘法逆元,求乘法逆元不一定要用欧几里德,还可以用欧拉定理。
欧拉定理求逆元简介: ---维基
在数论中,欧拉定理(也称费马-欧拉定理或欧拉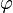 函数定理)是一个关于同余的性质。欧拉定理表明,若
函数定理)是一个关于同余的性质。欧拉定理表明,若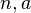 为正整数,且
为正整数,且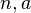 互素,
互素,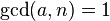 ,则
,则

其中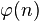 为欧拉函数,
为欧拉函数,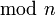 为同余关系。欧拉定理得名于瑞士数学家莱昂哈德·欧拉。
为同余关系。欧拉定理得名于瑞士数学家莱昂哈德·欧拉。
欧拉定理实际上是费马小定理的推广。
以下是 http://blog.csdn.net/wukonwukon/article/details/7341270 的代码,加上我的一点注释:
/*
Pro: hdu-3037
Sol:Lucas
还用到乘法逆元,乘法逆元可以不用欧几里得
定义:
满足a*k≡1 (mod p)的k值就是a关于p的乘法逆元。
(PS:p一定是个素数才能对a有乘法逆元(除1),特别注意:当p是1时,对于任意a,k都为1)
为什么要有乘法逆元呢?
当我们要求(a/b) mod p的值(a/b一定是个整数),且a很大,无法直接求得a/b的值时,我们就要用到乘法逆元。
我们可以通过求b关于p的乘法逆元k,将a乘上k再模p,即(a*k) mod p。
其结果与(a/b) mod p等价。
date:2012/08/07
*/
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
#define N 100010
long long mod_pow(int a,int n,int p)
{
long long ret=1;
long long A=a;
while(n)
{
if (n & 1)
ret=(ret*A)%p;
A=(A*A)%p;
n>>=1;
}
return ret;
}
long long factorial[N];
void init(long long p)
{
factorial[0] = 1;
for(int i = 1;i <= p;i++)
factorial[i] = factorial[i-1]*i%p;
}
long long Lucas(long long a,long long k,long long p)
//求C(n,m)%p p最大为10^5。a,b可以很大!
{
long long re = 1;
while(a && k)
{
long long aa = a%p;long long bb = k%p;
if(aa < bb) return 0; //C(aa,bb) 表示 在aa里面取bb个,取法为0;
//由于p是素数,所以 a / b % p ,b 对于 mod a 肯定存在逆元
re = re*factorial[aa]*mod_pow(factorial[bb]*factorial[aa-bb]%p,p-2,p)%p;//这儿的求逆不可先处理
a /= p;
k /= p;
}
return re;
}
int main(){
int a,b,c;
while(cin >> a >> b >> c){
cout << mod_pow(a,b,c)<< endl;
}
return 0;
}
int main()
{
int t;
cin >> t;
while(t--)
{
long long n,m,p;
cin >> n >> m >> p;
init(p);
cout << Lucas(n+m,m,p) << "\n";
}
return 0;
}
http://acm.hdu.edu.cn/showproblem.php?pid=4349
官方解题报告,懂了Lucas就非常非常非常好写代码了。
本题为Lucas定理推导题,我们分析一下 C(n,m)%2,那么由lucas定理,我们可以写
* 成二进制的形式观察,比如 n=1001101,m是从000000到1001101的枚举,我们知道在该定理中
* C(0,1)=0,因此如果n=1001101的0对应位置的m二进制位为1那么C(n,m) % 2==0,因此m对应n为0的
* 位置只能填0,而1的位置填0,填1都是1(C(1,0)=C(1,1)=1),不影响结果为奇数,并且保证不会
* 出n的范围,因此所有的情况即是n中1位置对应m位置0,1的枚举,那么结果很明显就是:2^(n中1的个数)
/*
Pro: hdu-4349
Sol: lucas
date: 2012/08/07
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
#include <set>
#include <vector>
using namespace std;
int n,sum ;
int main(){
while(scanf("%d",&n) != EOF){
sum = 0;
while(n){
sum += (n & 1);
n >>= 1;
}
printf("%d\n", (1 << sum));
}
return 0;
}










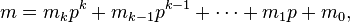
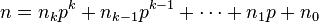

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








