神经网络中的参数的求解：前向和反向传播算法

最新推荐文章于 2024-02-29 10:51:25 发布

junmuzi

最新推荐文章于 2024-02-29 10:51:25 发布

阅读量4.8k

点赞数

分类专栏： caffe

caffe 专栏收录该内容

45 篇文章 0 订阅

订阅专栏

original url:

http://www.cnblogs.com/happylion/p/4193527.html

For more info: you could ref the book《Pattern Recognition and Machine Learning》

神经网络最基本的知识可以参考神经网络基本知识，基本的东西说的很好了，然后这里讲一下神经网络中的参数的求解方法。

注意前一次的各单元不需要与后一层的偏置节点连线，因为偏置节点不需要有输入也不需要sigmoid函数得到激活值，或者认为激活值始终是1.

一些变量解释：

标上“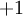 $\textstyle +1$ ”的圆圈被称为偏置节点，也就是截距项.

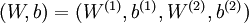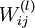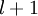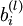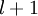本例神经网络有参数 $\textstyle (W,b) = (W^{(1)}, b^{(1)}, W^{(2)}, b^{(2)})$ ，其中 $\textstyle W^{(l)}_{ij}$ （下面的式子中用到）是第 $\textstyle l$ 层第 $\textstyle j$ 单元与第 $\textstyle l+1$ 层第 $\textstyle i$ 单元之间的联接参数（其实就是连接线上的权重，注意标号顺序）， $\textstyle b^{(l)}_i$ 是第 $\textstyle l+1$ 层第 $\textstyle i$ 单元的偏置项。

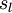用 $\textstyle s_l$ 表示第 $\textstyle l$ 层的节点数（偏置单元不计在内）

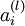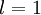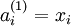用 $\textstyle a^{(l)}_i$ 表示第 $\textstyle l$ 层第 $\textstyle i$ 单元的激活值（输出值）。当 $\textstyle l=1$ 时， $\textstyle a^{(1)}_i = x_i$ ，也就是样本输入值的第 $\textstyle i$ 个特征。

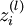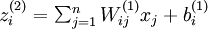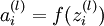用 $\textstyle z^{(l)}_i$ 表示第层各单元对第 $\textstyle l$ 层第 $\textstyle i$ 单元进行输入加权和（包括偏置单元），比如， $\textstyle z_i^{(2)} = \sum_{j=1}^n W^{(1)}_{ij} x_j + b^{(1)}_i$ ，所以 $\textstyle a^{(l)}_i = f(z^{(l)}_i)$ ，这里的f（.）就是激活函数，一般是sigmoid函数。

表示最后的输出量，如果网络最终输出是一个值，那么就是一个标量，如果最终输出不止一个值（样本的label y也是一个矢量），那么就是一个矢量。

对于上图：我们有

把这些公式利用向量变成另一中公式形式（激活函数 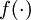$\textstyle f(\cdot)$ 也扩展为用向量（分量的形式）来表示，即 $\textstyle f([z_1, z_2, z_3]) = [f(z_1), f(z_2), f(z_3)]$ ）为：

这也就是我们把wij定义成上面那样的元素，这样直接根据wij的标号排成一个矩阵，而不用再变换或转置之类的了。

假设w和b已知的话，我们根据上两行的迭代公式不停的迭代就得到了神经网络里各个单元的激活值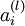 $\textstyle a^{(l)}_i$ 。

上面的计算步骤叫作前向传播。

因为我们w和b是不知道的，我们还得要通过训练学习到这些参数，那么我们怎么训练得到那？我们知道一些训练样本（注意这里里不一定是一个标量，而是），我们仍然使用梯度下降法来通过迭代得到收敛后的模型参数值。

我们在每一次迭代中，假设w和b是已知的，然后通过一次前向传播得到模型中激活值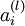 $\textstyle a^{(l)}_i$ 。

我们根据每一次迭代中模型最后输出的跟样本的标记做差平方（如果都是矢量的话，做差平方是向量里的各个元素分别对应做差然后平方和），然后求出所有样本的这些误差平方和。然后得到每一次迭代的cost function （含L2正则项）：

虽然这里每一个神经元类似于logistic回归模型，但是这里cost function中没用似然函数方法，还是利用的均方误差。其实这两种方法得到的结果是一样的（还记得利用似然函数求得的公式跟均方误差公式一样么）。类似的，在L2正则项中，参数不包括偏置参数，也就是常数项那些参数。

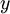模型中如果使用的激活函数是sigmoid函数，那么这个模型最后输出层里的每个节点输出的值都在(0,1)之间，那么样本的标记向量里的元素就要求在（0,1）之间，所以我们首先要用某种方法转变样本的标记范围（类似标准化，如果模型的激活函数使用的是tanh函数，那么这里就是采用的标准化转变样本标记值）（译者注：也就是 $\textstyle y$ ），以保证其范围为（0,1）之间。

我们有了cost function，接下来我们就需要最小化这个function，我们使用梯度下降法，也就是这俩公式：

……………………………………………………………………………………………………………………………………………………...(1)

但是我们这时候不能直接对cost function对每一个参数进行求偏导，因为这些参数都是相互关联的，没办法找到显式的偏导。我们只能曲线救国。我们怎么求偏导呢？我们使用反向传播算法求得，具体是这样的：

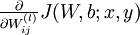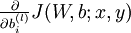我们不是一下对整个操作，而是每一个样本和通过模型得到的做差平方，视为小，也就是，我们每一次处理一个样本的cost function，使用反向传播算法来计算 $\textstyle \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y)$ 和 $\textstyle \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y)$ ，一旦我们求出每个样本的该偏导数，就可以推导出整体代价函数 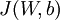$\textstyle J(W,b)$ 的偏导数：

………………………………………………………………………………………………………..(2)

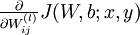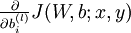下面接着说我们怎么求每一个样本的 $\textstyle \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y)$ 和 $\textstyle \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y)$ 。

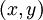给定一个样例 $\textstyle (x,y)$ ，我们首先进行“前向传导”运算，计算出网络中所有的激活值，包括 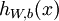$\textstyle h_{W,b}(x)$ 的输出值。

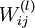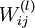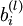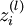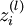这时候我们不把单个的 $\textstyle W^{(l)}_{ij}$ 看成输入量，而是把每一个单元的所有 $\textstyle W^{(l)}_{ij}$ 和 $\textstyle b^{(l)}_i$ 叠加和 $\textstyle z^{(l)}_i$ 看成输入，于是我们看成对 $\textstyle z^{(l)}_i$ 求偏导。

求出的偏导分别叫每个单元的“残差” 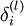$\textstyle \delta^{(l)}_i$ ，具体如下：

（1）最后一层（输出层）单元的残差：

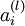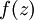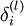我们通过前向传播算法求出了网络中所有的激活值 $\textstyle a^{(l)}_i$ ，这个也是可以求出来的，比如当 $\textstyle f(z)$ 是sigmoid函数，那么，所以这个残差 $\textstyle \delta^{(l)}_i$ 就求出来了。就是这个cost function J(W,b;x,y)对求导。

（2）接下来我们求 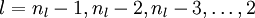$\textstyle l = n_l-1, n_l-2, n_l-3, \ldots, 2$ 的各个层单元的残差：

先求l= 各单元的残差：

因为等于，所以红框里面就是一个复合函数求导。

倒数第三个到倒数第二个公式只有k=i的时候求导存在，wij是个系数，所以这一步也很好理解。

最后结果中的代表的意义是：

然后再乘以，就是。

再求l= 各个层单元的残差：

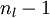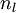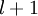将上式中的 $\textstyle n_l-1$ 与 $\textstyle n_l$ 的关系替换为 $\textstyle l$ 与 $\textstyle l+1$ 的关系，就可以得到

这时候每个单元的残差就求出来了，接下来计算我们需要的偏导数，计算公式如下：

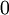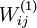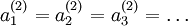求出每个样本cost function的各个偏导后，我们就能根据公式（2）求出所有整个cost function的各个偏导了。那么再根据公式（1），我们就求出了这一次梯度下降法迭代后的参数，然后我们不停的迭代，最终就找到了参数的收敛值。这里需要强调的是，一开始要将参数进行随机初始化，不是全部置为 $\textstyle 0$ 。如果所有参数都用相同的值作为初始值，那么所有隐藏层单元最终会得到与输入值有关的、相同的函数（也就是说，对于所有 $\textstyle i$ ， $\textstyle W^{(1)}_{ij}$ 都会取相同的值，那么对于任何输入 $\textstyle x$ 都会有： $\textstyle a^{(2)}_1 = a^{(2)}_2 = a^{(2)}_3 = \ldots$ ）。随机初始化的目的是使对称失效。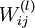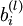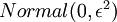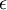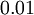为了求解神经网络，我们需要将每一个参数 $\textstyle W^{(l)}_{ij}$ 和 $\textstyle b^{(l)}_i$ 初始化为一个很小的、接近零的随机值（比如说，使用正态分布 $\textstyle {Normal}(0,\epsilon^2)$ 生成的随机值，其中 $\textstyle \epsilon$ 设置为 $\textstyle 0.01$ ）

参考： http://deeplearning.stanford.edu/wiki/index.php/反向传导算法

junmuzi

关注

0
点赞
踩
3

收藏

觉得还不错? 一键收藏
1
评论
神经网络中的参数的求解：前向和反向传播算法

original url:http://www.cnblogs.com/happylion/p/4193527.htmlFor more info: you could ref the book《Pattern Recognition and Machine Learning》神经网络最基本的知识可以参考神经网络基本知识，基本的东西说的很好了，然后这里讲一下神
复制链接

扫一扫