Ural 1554. Multiplicative Functions 狄利克雷卷积

1554. Multiplicative Functions

Time limit: 2.0 second
Memory limit: 64 MB

In number theory, a multiplicative function is an arithmetic function  F( n) of the positive integer  nwith property that  F(1) = 1 and whenever  a and  b are coprime  (gcd( a,  b) = 1),  then  F( ab) =  F( a) F( b).

The function  E( n) defined by  E( n) = 1 if  n = 1 and = 0 if  n > 1, is sometimes called  multiplication unit for Dirichlet convolution or simply the unit function. If  F and  G are two multiplicative functions, one defines a new multiplicative function  F  *  G, the Dirichlet convolution of  F and  G, by

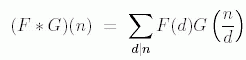
where the sum extends over all positive divisors  d of  n. With this operation, the set of all multiplicative functions turns into an abelian group; the identity element is  E. 

from  Wikipedia, the free encyclopedia

In this task you have to find the inverse of a multiplicative function. To cope with overflow problem, we define arithmetic functions as:  F:  N  —>   Z 2007 where  N is the set of positive integers, and  Z 2007 is a residue ring (ring of integers 0–2006, where arithmetic operations + and × are performed modulo 2007). Function  G is called the inverse of function  F if and only if  F  *  G =  G  *  F=  E.

You are given the first  N values of function  F, you need to find the first  N values of the inverse function  G.

Input

In the first line of the input one number  N is written (1 ≤  N ≤ 10 4). In the second line values F(1),  F(2),  F(3), …,  F( N) are listed. Numbers are separated by spaces. (Each value is nonnegative and doesn't exceed 2006.)

Output

In the first line of the output print first  N values of inverse function  G, separated by spaces: G(1),  G(2), …,  G( N).

Sample

input	output
16 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	1 2006 2006 0 2006 1 2006 0 0 1 2006 0 2006 1 1 0

Problem Source: Novosibirsk SU Contest. Petrozavodsk training camp, September 2007

题意：
给出算数函数f(n)（mod 2007）求它的逆函数g(n)（mod 2007）。

在算术函数集上，可以定义一种二元运算，使得取这种运算为乘法，取普通函数加法为加法，使得算术函数集为一个交换环。其中一种这样的运算便是狄利克雷卷积。它和一般的卷积有不少相类之处。

对于算术函数，定义其狄利克雷卷积。

取狄利克雷卷积为运算，积性函数集是算术函数集的子群。

的值如下：

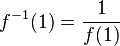
对于 ，

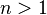默比乌斯函数μ的逆函数为（一般意义上的）1，即对于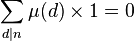，。这是默比乌斯反转公式的原理。

狄利克雷卷积以数学家狄利克雷命名。1857年刘维尔曾发表了许多包含这个运算的恒等式。将它视为二元运算这个观点是E. T. 贝尔和 M. Cipolla 在1915年提出的。

参考链接： http://zh.wikipedia.org/wiki/%E7%8B%84%E5%88%A9%E5%85%8B%E9%9B%B7%E5%8D%B7%E7%A9%8D

http://blog.csdn.net/jsun_moon/article/details/9893541

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
int f[10001],g[10001],n,fi;
int mod(int a,int b)
{
    if(a>=0)return a%b;
    return (a%b+b)%b;
}
void solve(int i)
{
    if(i==1)
    {
        g[i]=1/f[1];
        return;
    }
    int d[100],nd=0,sum=0;
    for(int k=1,b=sqrt((float)i); k<=b; k++)
    {
        if(i%k==0)
        {
            if(i/k!=k&&k!=1)
            {
                d[nd++]=k;
                d[nd++]=i/k;
            }
            else d[nd++]=k;
        }
    }
    sort(d,d+nd);
    for(int j=0; j<nd; j++)
    {
        sum=sum+g[d[j]]*f[i/d[j]];
    }
    g[i]=mod(-g[1]*sum,2007);
}
int main()
{
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&f[i]);
    }
    for(int i=1; i<=n; i++)
    {
        solve(i);
        if(i==1)
            printf("%d",g[i]);
        else
            printf(" %d",g[i]);
    }
    printf("\n");
    return 0;
}