排序(2) 分治与归并排序

最新推荐文章于 2022-12-28 19:49:25 发布

Lurfee

最新推荐文章于 2022-12-28 19:49:25 发布

阅读量1.8k

点赞数 1

分类专栏：算法文章标签：算法实例递归归并排序

本文链接：https://blog.csdn.net/l597692583/article/details/51131694

版权

算法专栏收录该内容

9 篇文章 0 订阅

订阅专栏

分治法主要思想

基本思想：归并排序用了分治的思想。所谓分治法，顾名思义分而治之。将原问题分解为几个规模较小的但类似原问题的子问题，然后算法多次递归的调用自身以解决这些紧密相关的若干子问题，然后再合并这些子问题的解来建立原问题的解。

分治法(Divide and Conquer)解决问题遵循三个步骤：
①：分解原问题为若干子问题，这些子问题是原问题的规模较小的实例。
②：解决这些子问题，递归求解这些子问题。若子问题规模足够小，则直接求解。
③：合并这些子问题的解构成原问题的解。

归并排序的实现

归并排序遵循分治思想：
①：分解n个元素的待排序列为2个各具n/2个元素的待排序列。
②：使用归并排序递归的排序两个子序列。
③：合并两个已排序的子序列的结果。
归并排序的关键点在于合并子序列结果。

下面是归并排序的python实现，其中包括了合并子过程：

#合并操作
def merge(A,first,mid,last):
    L = A[first : mid+1]  #把A[first],...,A[mid]依次复制给左子数组L
    R = A[mid+1 : last+1] #把A[mid+1],...,A[last]依次复制给右子数组R
    i = j = 0
    k = first
    while i < len(L) and j < len(R): #将L,R中的记录由小到大的并入A中
        if L[i] <= R[j]:
            A[k] = L[i]
            i += 1
        else:
            A[k] = R[j]
            j += 1
        k += 1
    while i < len(L): #将L中剩余记录并入A中
        A[k] = L[i]   #C++中可以写成A[k++] = L[i++]，一句顶三
        i += 1
        k += 1
    while j < len(R): #将R中剩余记录并入A中
        A[k] = R[j]
        j += 1
        k += 1

#Merge Sort , T = O(nlgn)
def MergeSort(A,first,last):
    if first < last:
        mid = (first+last) >> 1
        MergeSort(A,first,mid)
        MergeSort(A,mid+1,last)
        merge(A,first,mid,last)

合并操作的代码很简单，过程基本一目了然。这里图示说明一下：
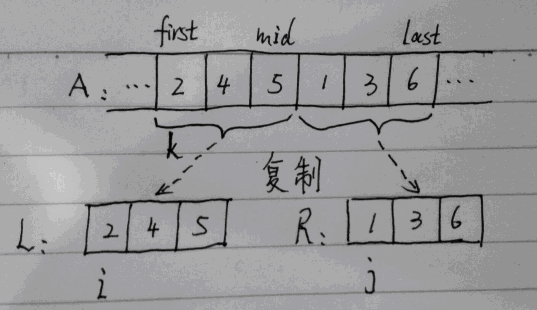
这里写图片描述
初始状态如图，第一次执行的时候L[i] > R[j] 所以把R[j]复制给A[k],然后递增j和k的值，第二次的时候L[i] < R[j]，把L[i]复制给A[k],然后递增i和k的值，以此循环，直到L和R中任有一个数组复制完，然后将另一个数组依次复制到A数组中，至此结束。

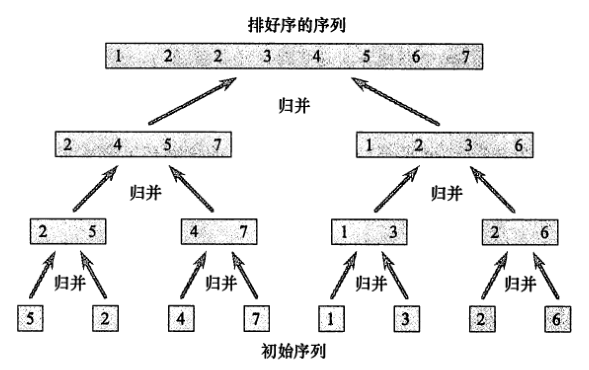
整个算法执行的递归轨迹图如下：

归并排序性能评价

归并排序是稳定的，任何情况下的时间复杂度均为O(nlgn)，但是需要O(n)的额外辅助空间以及需要递归调用自身。实际情况中，若是大规模问题，O(n)的额外空间开销值得思考。另外虽然递归能在解决问题时展现清晰的思路，但是平时能用循环代替递归、能避免递归调用则尽量避免，这皆因递归调用本身有效率问题，甚至有造成栈溢出的风险。

改进和拓展

上述python实现的是二路归并排序。改进的方面有多路归并、归并排序的非递归算法、当问题规模分解的足够小时用插入排序。《算法4(塞克威奇)》中还提到检测待合并数组段是否有序(当A[mid]<=A[mid+1]时)和通过递归中交换参数避免数组复制来改进，个人认为这属于编码层面的改进，这里暂不讨论，但是实现也非常简单。这里主要简要说一下非递归版归并排序和加快小数组排序的归并排序。

非递归版本的归并排序在《算法4》中被称为自底向上的归并排序，其方法是直接从最小的序列开始归并，而省略了分解数组的步骤。
这里写图片描述
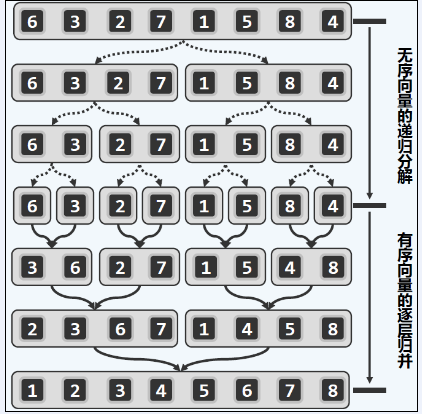
可与前面的图做比较，自底向上的过程省略了等分拆解的步骤，直接从两两归并开始直到所有元素有序。
下面是Python实现：

#自底向上的归并排序的实现
def MergeSortBottomUp(A,first,last):
    if first > last:
        return False

    n = last-first+1 #数组元素个数
    i = 2            #从2开始的两两归并，2,4,8,16,...,2^n
    while i < 2*n:
        j = first
        while True:
            mid = (j + j+i-1) >> 1 #j,j+i-1 分别为待合并子数组的首末元素下标
            if j+i-1 < last:
                merge(A,j,mid,j+i-1)
                j += i
            else:
                merge(A,j,mid,last)
                break
        i <<= 1
    return True

另外一个改进是对小数组运用直接插入排序来提升整体效率，代码如下：

#优化后的归并排序。
def MergeSortWithInsertionSort(A,first,last,m=0):
    if first + m < last:
        mid = (first+last)>>1
        MergeSortWithInsertionSort(A,first,mid,m)
        MergeSortWithInsertionSort(A,mid+1,last,m)
        merge(A,first,mid,last)
    else:
        InsertionSort(A,first,last)

将数组递归分解至m长度的小数组时，运用直接插入排序，然后对有序的小数组合并，一层一层回溯，直到全部有序。m的最佳值为lgn，n为数组规模，可以参考《算法导论》相关例题得证。

渐进复杂度分析

为什么渐进复杂度是O(nlgn)？如何得出？归并排序包含对自身的递归调用，基于此，我们可以用递归式来表示规模为n的问题上的总运行时间，然后解出递归式。

假设T(n)是规模为n的问题的总运行时间。如果问题规模足够小，那运行时间可以看成一个常数c,而如果问题规模比较大，可以把原问题分解成a个子问题，每个问题是原问题的1/b，求解一个规模为n/b的子问题需要T(n/b)的时间，所以需要aT(b/n)的时间求解a个子问题。如果分解问题的时间为D(n),合并子问题解的时间为C(n),假设忽略规模足够小的问题，那么得到的递归式为：T(n) = aT(n/b)+D(n)+C(n)

这里，归并排序，分解步骤仅仅计算数组中间位置，所以需要常数时间c。我们递归地解决 2个规模为n/2的子问题总共需要2T(n/2)的时间。对于合并步骤，需要O(n)的时间。简化一下可以得到归并排序的递归式：
T(n) = 2T(n/2)+cn

有了递归式，下一步就是求解递归式。《算法导论》中提到三种求解递归式的方法：

①：代入法。猜测一个解，运用数学归纳法证明这个解。
②：主方法。利用特定公式求解递归式。
前面两个方法请大家自行参见《算法导论》，这里不再多说，毕竟我更关注偏向工程与实用性的东西。

③：递归树法。个人比较喜欢的方法。比如对于归并排序的递归式，可以写成T(n) = T(n/2)+T(n/2)+cn
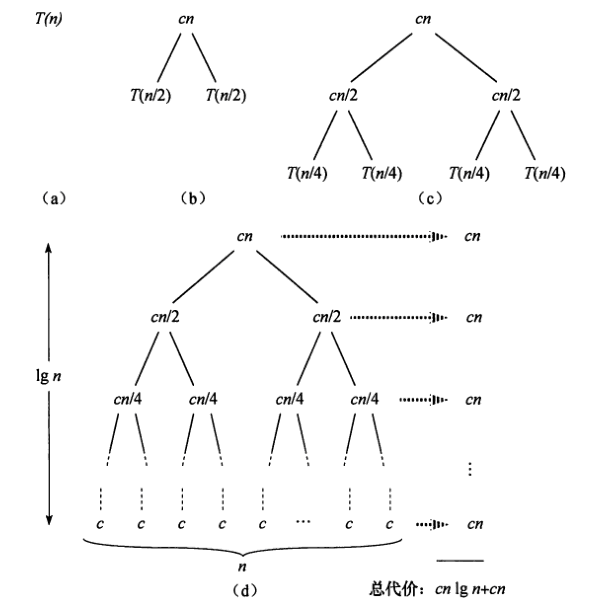
用递归树等价表示图如下：
这里写图片描述

图(b)是图(a)的等价树，递归一下，图(c)又是图(b)的等价树。以此类推，直到递归到最后一层，图(d)中，等价树高度为lgn, 每一层代价总和为cn, 所以渐进时间复杂度T(n) = O(nlgn)。

几个问题

①：二分查找。写出二分查找的递归和非递归代码，分析二分查找复杂度。

#二分查找递归版
def BinarySearchRec(A,key,first,last):
    if first > last:
        return False
    else:
        mid = (first+last) >> 1
        if A[mid] == key:
            return True
        elif A[mid] < key:
            return BinarySearchRec(A,key,mid+1,last)
        else:
            return BinarySearchRec(A,key,first,mid-1)

#二分查找非递归版
def BinarySearchLoop(A,key,first,last):
    while first <= last:
        mid = (first+last) >> 1
        if A[mid] == key:
            return True
        elif A[mid] < key:
            first = mid+1
        else:
            last = mid-1
    return False

二分查找的分析很简单，其递归式为T(n) = T(n/2) + c
用递归树法或者主方法，得出T(n) = O(lgn)。二分查找可以说是分治法，也可以说是减治法的典型体现。

②：给定n个整数的集合S和一个整数x,确定S中是否存在两个整数之和刚好等于x。再拓展下，确定S中是否存在m个整数之和刚好等于x，若存在，找出所有的这些数。
第一个小问题，如果朴素方法求解，复杂度为O(n^2)
如果先对集合S排序，再利用二分查找的方法，可以把复杂度降到O(nlgn),代码如下：

#找出A数组中是否存在两数之和等于keySum
def Find2Sum(A,keySum):
    MergeSort(A,0,len(A)-1)
    for i in range(len(A)):
        key = keySum - A[i]
        if BinarySearchLoop(A,key,i+1,len(A)-1):
            return True
    return False

至于拓展问题，以后说到NP问题再来说。

③：逆序对问题。假如A[1,2,…,n]是一个有n个不同数的数组，若i小于j且A[i]大于A[j],则对偶(i,j)称为A的一个逆序对。实现一个算法确定A中逆序对个数。
按照题意，朴素算法复杂度是O(n^2)，这里利用分治思想，修改归并排序的算法可在O(nlgn)内解决。在合并步骤，计算每次合并逆序对个数，最后将结果汇总。代码如下：

#合并操作时计算逆序对个数
def mergeInversionPair(A,first,mid,last):
    L = A[first : mid+1]
    R = A[mid+1 : last+1]
    i = j = inversionPairCount = 0
    k = first
    while i < len(L) and j < len(R):
        if L[i] <= R[j]:
            A[k] = L[i]
            i += 1
        else:
            A[k] = R[j]
            j += 1
            inversionPairCount += (len(L)-i) #这里计算逆序对个数
        k += 1
    while i < len(L):
        A[k] = L[i]
        i += 1
        k += 1
    while j < len(R):
        A[k] = R[j]
        j += 1
        k += 1  
    return inversionPairCount

#计算总的逆序对个数
def CountInversionPair(A,first,last):
    if first < last:
        mid = (first+last)>>1
        c1 = CountInversionPair(A,first,mid)
        c2 = CountInversionPair(A,mid+1,last)
        c3 = mergeInversionPair(A,first,mid,last)
        return c1+c2+c3
    else:
        return 0

当然也可以用非递归版归并排序的去改进，这里不再多说。

④：找出一个数组中和值最大的子数组。
法一：朴素方法，找出所有子数组的组合，求得最大和值的子数组。T(n)=O(n^2)

#最大子数组和暴力解法
def FindMaxmumSubArrayNaive(A,first,last):
    if first > last:
        return 0,-1,-1

    start = end = first
    maxSum = A[first]
    for i in range(first,last+1):
        subSum = 0
        for j in range(i,last+1):
            subSum += A[j]
            if maxSum < subSum:
                maxSum, start, end = subSum, i, j
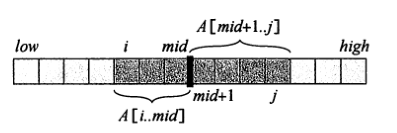
    return maxSum, start, end

法二：分治法求解。找到数组中点，将数组分解成左右子数组。和值最大的子数组要么在左子数组内，要么在右子数组内，要么是跨越中点的子数组。我们可以递归求解左右子数组中的最大子数组，剩下的问题就是求解跨越中点的最大子数组。

如上图，A[i,…,j]是跨越中点的最大子数组，它是由A[i,…,mid]和A[mid+1,…,j]组成，基于此，实现如下：

#找出跨越中点的最大子数组，返回最大子数组的和，首末下标。
def FindMaxmumSubArrayCrossMid(A,first,mid,last):
    start = mid
    end = mid+1
    leftMax = A[start]
    rightMax = A[end]
    subSum = 0
    for i in range(mid,first-1,-1): #等价于 for i in [mid,mid-1,...,0]
        subSum += A[i]
        if leftMax < subSum:
            leftMax = subSum
            start = i
    subSum = 0
    for j in range(mid+1,last+1): #等价于 for i in [mid+1,mid+2,...,last]
        subSum += A[j]
        if rightMax < subSum:
            rightMax = subSum
            end = j
    return leftMax+rightMax, start, end

#求解最大子数组的分治法，返回最大子数组的和值与首末下标。
def FindMaxmumSubArrayRec(A,first,last):
    if first < last:
        mid = (first+last)>>1
        leftMax,leftStart,leftEnd = FindMaxmumSubArrayRec(A,first,mid)
        rightMax,rightStart,rightEnd = FindMaxmumSubArrayRec(A,mid+1,last)
        crossMax,start,end = FindMaxmumSubArrayCrossMid(A,first,mid,last)
        if leftMax >= rightMax and leftMax >= crossMax:
            return leftMax, leftStart,leftEnd
        elif rightMax >=leftMax and rightMax >= crossMax:
            return rightMax,rightStart,rightEnd
        else:
            return crossMax,start,end
    elif first == last:
        return A[first],first,first
    else:
        return 0,-1,-1

该算法递归式为：T(n)=2T(n/2)+cn,解递归式，得T(n)=O(nlgn)

法三：根据该问题的特征，我们发现,任何包含和值小于0的子数组的子数组必然不是原数组的最大子数组(这算是一个隐含的已知量。再说点题外话，推荐大家看下波利亚的《如何解题》，《代码大全》与《暗时间》的作者皆有推荐。我从《如何解题》收获最大的是如何在大脑里正确的构建解题思路、丰富解题思路，而非具体方法)，根据这点，可以减少很多不必要的计算，有点像减枝搜索这么个意思,时间复杂度为O(n),代码实现如下：

#最大子数组问题 O(n) 实现
def FindMaxmumSubArrayLoop(A,first,last):
    if first > last: #空数组的情况
        return 0,-1,-1

    subSum = 0
    startPos = first
    maxSubSumRet = (0,0,0) #(最大子数组和值，开始下标，结束下标)

    for i in range(first,last+1):
        subSum += A[i]
        if subSum < 0:
            subSum = 0
            startPos = i+1
        else:
            if maxSubSumRet[0] < subSum:
                maxSubSumRet = (subSum,startPos,i)

    if not maxSubSumRet[0]: #如果所有数皆不大于0，返回第一个最大值。
        maxSubSumRet = (A[first],first,first)
        for i in range(first+1,last+1):
            if maxSubSumRet[0] < A[i]:
                maxSubSumRet = (A[i],i,i)

    return maxSubSumRet