Beta 分布的应用

从随机变量到顺序统计量

考虑如下的游戏：有一个魔盒（随机数生成器），上有一个按钮，每按一下按钮，就均匀地输出一个 $U\sim[0,1]$之间的随机数，现在按上下，得到10个随机数，第7大的数是多少？我更进一步发问，第7大的数，要求猜测不超过0.01才算对。

对上面的游戏作如下的数学抽象：

1. $X_1,X_2,\cdots,X_n \sim^{iid} U(0,1)$
2. 把这 $n$ 个随机变量排序后得到的顺序统计量$X_{(1)},X_{(2)},\ldots,X_{(n)}$
3. 问 $X_{(k)}$的分布是什么？

对于上面的游戏而言 $n=10,k=7$，如果我们能求出 $X_{(7)}$的分布的概率密度，那么用概率密度的极值点取做猜测是最好的策略。对于一般的情形，$X_{(k)}$的分布是什么呢？那么我们尝试计算 $X_{(k)}$ 落在区间 $[x,x+\Delta x]$ 的概率，也即求如下的概率值：

$$P(x\leq X_{(k)}\leq x+\Delta x)=?$$

把 $[0,1]$区间内分为三段 $[0, x), [x,x+\Delta x],(x+\Delta x, 1]$，我们首先考虑简单的情形（这不正是数学研究的基本方法论吗，从简单到复杂），假设 $n$ 个数中只有一个落在了区间 $[x,x+\Delta x]$内，则因为要求这个区间的数 $X_{(k)}$是第 $k$大的，
- 则 $[0, x)$中应该有 $k-1$个数，
- $(x+\Delta x]$这个区间中应该有 $n-k$个数。
不失一般性的，我们先考虑如下的一个符合上述要求的事件 $E$：

$$\begin{split} E=\{ & X_1\in [x,x+\Delta x],\\ & X_i\in [0, x)\quad (i=2,\cdots,k),\\ & X_j\in (x+\Delta x,1] \quad (j=k+1,\cdots,n)\} \end{split}$$

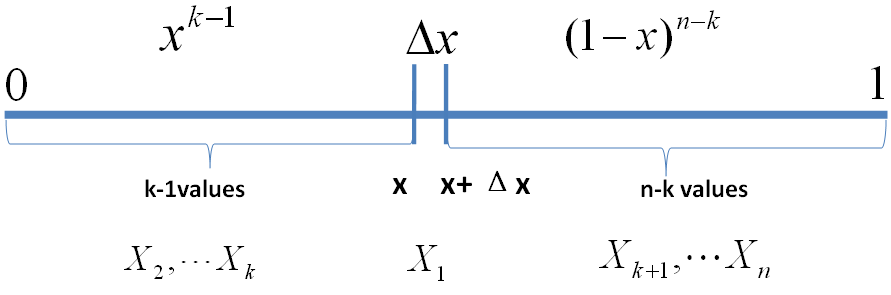
则有：
$$\begin{split} P(E)=&\prod_{i=1}^nP(X_i)\\ =&x^{k-1}(1-x-\Delta x)^{n-k}\Delta x \end{split}$$
对 $(1-x-\Delta x)^{n-k}$应用二项展开，也即：
$$\begin{split} (1-x-\Delta x)^{n-k}=&\binom{n-k}{0}(1-x)^{n-k}(-\Delta x)^0+\binom{n-k}{1}(1-x)^{n-k-1}(-\Delta x)^1+\cdots+\binom{n-k}{n-k}(1-x)^0(-\Delta x)^{n-k}\\ =&(1-x)^{n-k}+o(\Delta x) \end{split}$$
其中 $o(\Delta x)$表示 $\Delta x$的高阶无穷小，所以，可对 $P(E)$，继续展开得：
$$\begin{split} P(E)=&\prod_{i=1}^nP(X_i)\\ =&x^{k-1}(1-x-\Delta x)^{n-k}\Delta x\\ =&x^{k-1}\left [(1-x)^{n-k}+o(\Delta x)\right ]\Delta x\\ =&x^{k-1}(1-x)^{n-k}\Delta x \end{split}$$
再来考虑这之中的组合数，也即 $n$个数中有一个落在 $[x,x+\Delta x]$ 区间得有 $n$中取法，余下的 $n-1$个数中有 $k-1$个落在 $[0,x)$的有 $\binom{n-1}{k-1}$中组合，故与事件 $E$等价的事件一共有 $n\binom{n-1}{k-1}$个。

继续考虑稍微复杂一点的情形，假设 $n$ 个数有两个数落在了区间 $[x,x+\Delta x]$，

$$\begin{split} E'=\{&X_1,X_2\in [x,x+\Delta x],\\ &X_i\in [0,x)\quad (i=3,4,\ldots,k) \\ & X_j\in (x+\Delta x,1]\quad (j=k+1,\ldots,n)\} \end{split}$$
则有：
$$P(E')=x^{k-2}(1-x-\Delta x)^{n-k}(\Delta x)^2=o(\Delta x)$$
从以上的分析我们很容易看出，只要落在 $[x,x+\Delta x]$内的数字超过一个，则对应的事件的概率就是 $o(\Delta x)$。于是：
$$\begin{split} P(x\leq X_{(k)}\leq x+\Delta x)=&n\binom{n-1}{k-1}P(E)\\ =&n\binom{n-1}{k-1}x^{k-1}(1-x)^{n-k}\Delta x+o(\Delta x) \end{split}$$
所以可以得到 $X_{(k)}$的概率密度为：
$$\begin{split} P(X_{(k)})=&\lim_{\Delta x\to 0}\frac{P(x\leq X_{(k)}\leq x+\Delta x)}{\Delta x}\\ =&n\binom{n-1}{k-1}x^{k-1}(1-x)^{n-k}\\ =&\frac{n!}{(k-1)!(n-k)!}x^{k-1}(1-x)^{n-k}\quad x\in [0,1] \end{split}$$
利用Gamma函数，我们可以把 $f(x)$表达为：
$$f(x)=\frac{\Gamma(n+1)}{\Gamma(k)\Gamma(n-k+1)}x^{k-1}(1-x)^{n-k}$$

还记得神奇的Gamma函数可以把许多数学概念从整数集合延拓到实数集合。
我们记 $\alpha=k,\beta=n-k+1$，于是我们得到：

$$P(X_{(k)})=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}$$
这就是一般意义上的Beta分布。
好，我们回到开始的游戏， $n=10,k=7$，我们按照如下的密度分布的峰值取猜测是最有把握的：
$$f(x)=\frac{10!}{6!3!}x^6(1-x)^3\quad x\in[0,1]$$