2014年参加数学建模美赛, 其中一道题是选出5大优秀教练,数据来源要求自行寻找。 在比赛中,我们运用了层次分析法(AHPAnalytic Hierarchy Process)进行建模,好不容易理解了这一方法的思想,在自己的博客里记录一下,希望可以帮助初次接触层次分析法的人,更快地理解这一的整体思想,也利于进一步针对细节进行学习。文章内容主要参阅 《matlab数学建模算法实例与分析》,部分图片来源于WIKI
文章分为2部分:
1第一部分以通俗的方式简述一下层次分析法的基本步骤和思想
2第二部分介绍一下我们队伍数学建模过程中,对层次分析法的应用,中间有些地方做了不严谨的推理,例如关于一致性的检验,如有人发现不正确,希望可以指正
第一部分:
层次分析法(Analytic Hierarchy Process ,简称 AHP )是对一些较为复杂、较为模糊的问题作出决策的简易方法,它特别适用于那些难于完全定量分析的问题。它是美国运筹学家T. L. Saaty 教授于上世纪 70 年代初期提出的一种简便、灵活而又实用的多准则决策方法。
人们在进行社会的、经济的以及科学管理领域问题的系统分析中,面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。
运用层次分析法建模,大体上可按下面四个步骤进行:
(i )建立递阶层次结构模型;
(ii )构造出各层次中的所有判断矩阵;
(iii )层次单排序及一致性检验;
(iv )层次总排序及一致性检验。
这四个步骤中,前两个步骤最容易理解,后两个步骤需要一点时间理解
首先从层次结构模型说起
层次分析法是用来根据多种准则,或是说因素从候选方案中选出最优的一种数学方法
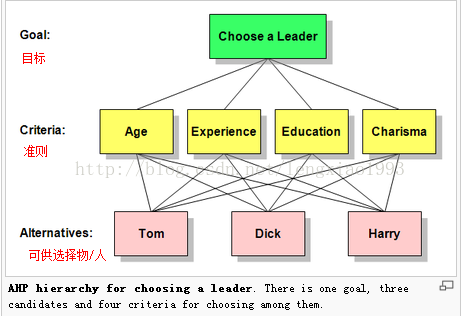
最顶层是我们的目标,比如说选leader,选工作,选旅游目的地
中间层是判断候选方物或人优劣的因素或标准
选工作时有:发展前途 ,待遇 ,工作环境等
选leader时有:年龄,经验,教育背景,魅力
在分层以后,为了选出最优候选
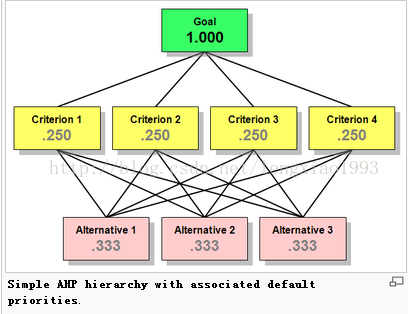
给目标层分配值1.000
然后将这一值作为权重,分配给不同因素,对应因素的权重大小代表该因素在整个选择过程中的重要性程度
然后对于候选方案,每一个标准再将其权重值分配给所有的候选方案,每一方案获得权重值,来源于不同因素分得的权重值的和
如下图:
目标层分配值为1, 然后我们给了4个候选方案评估标准 criterion 1 、 criterion 2、criterion 3、criterion 4
假设我们认为这四个标准同等重要, 于是目标层的值1 就被均分到 4个准则上, 每个准则获得的值为 0.25
然后我们从评估标准 criterion 1 出发, 考虑在该评估标准下, 3 个候选方案的优劣比如何。 假如我们认为在标准1 的衡量下, 3 个方案完全平等, 方案1 在该标准下的得分就应该是: 0.25 * (1/3)
同理, 如果我们假设剩下的 3 个标准下, 3个候选方案都是平分秋色, 那么方案 1 的最终得分就应该是
0.33 = 0.25 * (1/3) + 0.25 * (1/3) + 0.25 * (1/3) + 0.25 * (1/3)
最终获得的各个方案的的权重值的和依然为1
这不就是一个简单的权重打分的过程吗?为什么还要层次分析呢。这里就有两个关键问题:
1每个准则(因素)权重具体应该分配多少
2每一个候选方案在每一个因素下又应该获得多少权重
这里便进入层次分析法的第二个步骤,也是层次分析法的一个精华(构造比较矩阵(判断矩阵)comparison matrix):
首先解决第一个问题:每个准则(因素)权重具体应该分配多少?
如果直接要给各个因素分配权重比较困难,在不同因素之间两两比较其重要程度是相对容易的
现在将不同因素两两作比获得的值aij 填入到矩阵的 i 行 j 列的位置,则构造了所谓的比较矩阵,对角线上都是1, 因为是自己和自己比
这个矩阵容易获得,我们如何从这一矩阵获得对应的权重分配呢
这里便出现了一个比较高级的概念,正互反矩阵和一致性矩阵
首先正互反矩阵的定义是:
我们目前构造出的矩阵很明显就是正互反矩阵
而一致性矩阵的定义是:
这里我们构造出的矩阵就不一定满足一致性,比如我们做因素1:因素2= 4:1 因素2:因素3=2:1 因素1:因素3=6:1(如果满足一致性就应该是8:1),我们就是因为难以确定各因素比例分配才做两两比较的,如果认为判断中就能保证一致性,就直接给出权重分配了
到了关键部分,一致性矩阵有一个性质可以算出不同因素的比例
这里的w就是我们想要知道的权重,所以通过 求比较矩阵的最大特征值所对应的特征向量,就可以获得不同因素的权重,归一化一下(每个权重除以权重和作为自己的值,最终总和为1)就更便于使用了。(实际上写这篇博客就是因为,重新翻了线代的书才好不容易理解这里的,就想记录下来)
这里补充一点线性代数的知识:
n阶矩阵有n个特征值,每个特征值对应一个n维特征列向量,特征值和特征向量的计算方法这里就省略了,反正书中的程序是直接用matlab 的eig函数求的
这里不能忘了,我们给出的比较矩阵一般是不满足一致性的,但是我们还是把它当做一致矩阵来处理,也可以获得一组权重,但是这组权重能不能被接受,需要进一步考量
例如在判断因素1,2,3重要性时,可以存在一些差异,但是不能太大,1比2重要,2比3 重要,1和3比时却成了3比1重要,这显然不能被接受
于是引入了一致性检验:
一致性的检验是通过计算一致性比例CR 来进行的
当 10 . 0 < CR 时,认为判断矩阵的一致性是可以接受的,否则应对判断矩阵作适当修正。
CI的值由判断矩阵计算获得,RI的值查表获得,具体的计算公式这里就略去,重点是理解为什么要做一致性检验
接下来解决第二个问题:每一个候选方案在每一个因素下又应该获得多少权重
这里则需要将不同候选方案,在不同因素下分别比较,具体的比较方法,还是使用比较矩阵,只不过之前准则层的比较矩阵比较的对象是因素,这里比较的是某一因素下,候选方案的优劣, n个因素则需构造出来n个比较矩阵
例如在工作环境的因素下,工作1与工作2相比为 :4:2,工作2与工作3=2:1 工作1:工作3=6:1.,这样构造一个矩阵,再用之前的一致性矩阵的方法就可以求出一个权重,然后相对应因素(这里是工作环境)所拥有的权值就可以按这个权重比例分配给不同候选物或人。
其他因素同理
至此两个问题就都得到了解决
最终将每个候选物、人从不同因素获得的权值求和,就可以得到不同候选对于目标层的权值大小,继而可以根据值的大小,来选出优劣
对于第一部分的总结:
- 通过对层次分析法的基本了解,不难发现层次分析法对人们的思维过程进行了加工整理,提出了一套系统分析问题的方法,为科学管理和决策提供了较有说服力的依据。
- 但很明显的缺点是,整个分析过程似乎都是依赖于人的主观判断思维,一来不够客观,二来两两比较全部人为完成,还是非常耗费精力的,尤其是当候选方案比较多的时候。
文章的第二部分:
层次分析法的变形应用(也可能本来就是这样用的,只不过参考书上没这样说,外语
论文没细看)解决最优教练选择问题
目标:选最优教练
准则:
- 职业生涯所带队伍的胜率
- 职业生涯所带队伍的胜场
- 从教时长(年)
- 职业生涯所带队伍获奖状况(化成分数)
候选: 众多教练
准则层比较矩阵获得
- 准则层的比较矩阵好构造 ,作6次两两比较,就可以获得4*4的比较矩阵
候选层比较矩阵
每一个准则对应下来的 候选层 已经有定量的数据了。 这里其实就不再需要候选层比较矩阵了, 因为有4000个教练的话, 得比4000*3999次,可以直接利用定量的数据计算权重。
- 例如“职业生涯所带队伍的胜场” 这一准则对应到每个教练都有直接相应数据的,例如教练 A, B, C 职业生涯所带队伍胜场数为 100,150, 90. 此时该准则下得到的分数, 就应当按照 10:5:9 的比例来进一步划分。
类似的,胜率准则 下就根据 “胜率” 计算权重分配比例。 从教时长准则下就根据 “从教时间的年数” 计算权重分配比例
这里又有两点可以注意:
1.不同因素下数据的量纲和性质不一样,直接用数据作比来分配,不一定合适,比如胜率越要接近1越难,0.7比胜率0.5 和胜率0.9比0.7 ,后者比值比前者小,这显然不合适。这里可以利用指数函数和对数函数对数据先做一次处理, 再作为权重分配的依据。
2.这里的用定量数据作比获得的矩阵显然满足一致性要求,不需要做一致性检验。以职业生涯所带队伍的胜场数为例,如果教练 A, B, C 职业生涯所带队伍胜场数为 100,150, 90。 那么 A:B :C 无论怎么作比, 都不会违反 10:15:9 的一致性。
综上就对层次分析法完成了定性定量结合的应用,以及对多个候选方案的比较(其实只是就是用程序控制数据作比,我们水平有限,能成功应用该方法已经不容易了)
很遗憾的是比赛时编写的代码存放的优盘不慎丢失, 没有办法把代码共享出来, 这里只能将书中的代码贴出。比赛建模时, 就是在这个代码基础上进行修改实现。 只要理解了下列代码,编写符合自己需求的程序, 应当是水到渠成的事。
matlab 代码(对应于文章第一部分选 Leader 的内容):
clc,clear
fid=fopen('txt3.txt','r');
n1=6;n2=3;
a=[];
for i=1:n1
tmp=str2num(fgetl(fid));
a=[a;tmp]; %读准则层判断矩阵
end
for i=1:n1
str1=char(['b',int2str(i),'=[];']);
str2=char(['b',int2str(i),'=[b',int2str(i),';tmp];']);
eval(str1);
for j=1:n2
tmp=str2num(fgetl(fid));
eval(str2); %读方案层的判断矩阵
end
end
ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标
[x,y]=eig(a); % matlab eig(a) 返回矩阵的特征值和特征向量, 这里的 x 为矩阵 a 的 n 个特征向量, y 为矩阵 a 的 n 个特征值
lamda=max(diag(y)); % eig 函数返回的 y 是矩阵形式保存的, dig(y) 提取对角线上的n 个特征值到一个数组中, 求出最大特征值 lamda
num=find(diag(y)==lamda); % 返回最大特征的索引
w0=x(:,num)/sum(x(:,num)); % x( :num) 为最大特征值所对应的那一列特征向量。 w0 中准则层计算出的 包含归一化后的n 个权重值
cr0=(lamda-n1)/(n1-1)/ri(n1)
for i=1:n1 % 循环 n 个维度, 针对每个维度, 都计算一次方案层的比较矩阵及其权重值
[x,y]=eig(eval(char(['b',int2str(i)])));
lamda=max(diag(y));
num=find(diag(y)==lamda);
w1(:,i)=x(:,num)/sum(x(:,num));
cr1(i)=(lamda-n2)/(n2-1)/ri(n2);
end
cr1, ts=w1*w0, cr=cr1*w0
txt3.txt 中的内容, 前6行为准则层的 6 x 6 比较矩阵, 后 18 行则为 6 个准则下, 各自的 3 x 3 的比较矩阵。
1 1 1 4 1 1/2
1 1 2 4 1 1/2
1 1/2 1 5 3 1/2
1/4 1/4 1/5 1 1/3 1/3
1 1 1/3 3 1 1
2 2 2 3 3 1
1 1/4 1/2
4 1 3
2 1/3 1
1 1/4 1/5
4 1 1/2
5 2 1
1 3 1/3
1/3 1 1/7
3 7 1
1 1/3 5
3 1 7
1/5 1/7 1
1 1 7
1 1 7
1/7 1/7 1
1 7 9
1/7 1 1
1/9 1 1
再上一段 JAVA 代码, 方便 JAVA 童鞋参考, 这部分仅仅展示了如何用JAVA 代码进行准则层比较矩阵计算 。
import org.apache.commons.math3.linear.*;
public class MatrixTester {
public static void main(String[] args) {
// Create a real matrix with two rows and three columns, using a factory
// method that selects the implementation class for us.
double[][] matrixData = { {1d, 1d, 1d, 4d, 1d, 1d/2d},
{1d, 1d, 2d, 4d, 1d, 1d/2d},
{1d, 1d/2d, 1d, 5d, 3d, 1d/2d },
{1d/4d, 1d/4d, 1d/5d, 1d, 1d/3d, 1d/3d },
{1d, 1d, 1d/3d, 3d, 1d, 1d },
{2d, 2d, 2d, 3d, 3d, 1d },
};
RealMatrix m = MatrixUtils.createRealMatrix(matrixData);
// One more with three rows, two columns, this time instantiating the
// RealMatrix implementation class directly.
double[][] matrixData2 = {{1d, 2d}, {2d, 5d}, {1d, 7d}};
RealMatrix n = new Array2DRowRealMatrix(matrixData2);
// Note: The constructor copies the input double[][] array in both cases.
// Now multiply m by n
// RealMatrix p = m.multiply(n);
// System.out.println(p.getRowDimension()); // 2
// System.out.println(p.getColumnDimension()); // 2
//
// // Invert p, using LU decomposition
// RealMatrix pInverse = new LUDecomposition(p).getSolver().getInverse();
RealMatrix D = new EigenDecomposition(m).getD();
RealMatrix V = new EigenDecomposition(m).getV();
for(int i=0; i<D.getRowDimension();i++)
{
System.out.println(D.getRowMatrix(i));
}
for(int i=0; i<V.getRowDimension();i++)
{
System.out.println(V.getRowMatrix(i));
}
// 特征值
double maxLamda;
int columIndexForMaxLamda=0;
maxLamda=D.getEntry(0,0);
for(int i =0, j=0; i<D.getRowDimension()&&j<D.getColumnDimension();i++,j=i)
{
double lamda = D.getEntry(i,j);
if(maxLamda<lamda)
{
maxLamda=lamda;
columIndexForMaxLamda = j;
}
System.out.println(lamda);
}
// 输出尚未做归一化 w1, w2, w3, w4, w5, w6 ,
System.out.println(V.getColumnMatrix(columIndexForMaxLamda));
}
}










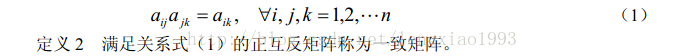

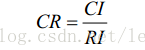













 1641
1641











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








