数据结构之时间复杂度和空间复杂度

 算法复杂度分为时间复杂度和空间复杂度，一个好的算法应该具体执行时间短，所需空间少的特点。

     随着计算机硬件和软件的提升，一个算法的执行时间是算不太精确的。只能依据统计方法对算法进行估算。我们抛开硬件和软件的因素，算法的好坏直接影响程序的运行时间。

     我们看一下小例子：

     int value = 0;                         // 执行了1次

     for (int i = 0; i < n; i++) {       // 执行了n次

          value += i;

     }

     这个算法执行了 1 + n 次，如果n无限大，我们可以把前边的1忽略，也就是说这个算法执行了n次

     时间复杂度常用大O符号表示，这个算法的时间复杂度就是O(n).

     概念： 一般情况下，算法的基本操作重复执行的次数是模块n的某一函数f(n),因此，算法的时间复杂度记做 T(n) = O(f(n))。 随着模块n的增大，算法执行的时间增长率f(n)的增长率成正比，所以f(n)越小，算法 的时间复杂度越低，算法的效率越高。

      计算时间复杂度

     1.去掉运行时间中的所有加法常数。

     2.只保留最高阶项。

     3.如果最高阶项存在且不是1，去掉与这个最高阶相乘的常数得到时间复杂度

 

我们看一个例子

     for (int i = 0; i < n; i++) {

          for (int j = i; j < n; j++) {

               // do .....

          }

     }

当 i = 0 时 里面的fo循环执行了n次，当i等待1时里面的for循环执行了n -  1次，当i 等于2里里面的fro执行了n - 2次........所以执行的次数是

根据我们上边的时间复杂度算法

     1.去掉运行时间中的所有加法常数： 没有加法常数不用考虑

     2.只保留最高阶项:　只保留 

     3. 去掉与这个最高阶相乘的常数:  去掉   只剩下 

     最终这个算法的时间复杂度为

 

再看一个线性的

      for ( int i = 0; i < n; i++) {

          // do .....

     }

     因为循环要执行n次所以时间复杂度为O(n)

 

其它的我也就不一个一个算了，下面给出了常用的时间复杂度

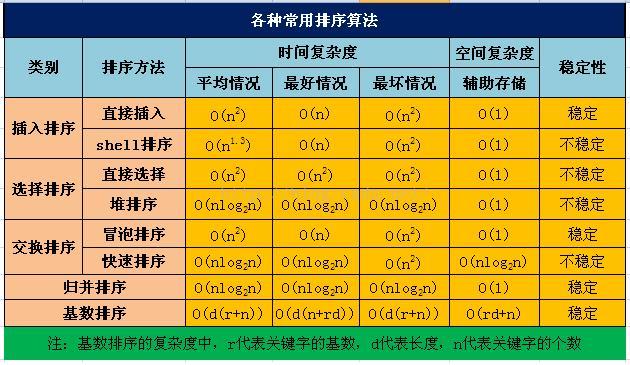
排序法	最差时间分析	平均时间复杂度	稳定度	空间复杂度
冒泡排序	O(n2)	O(n2)	稳定	O(1)
快速排序	O(n2)	O(n*log2n)	不稳定	O(log2n)~O(n)
选择排序	O(n2)	O(n2)	稳定	O(1)
二叉树排序	O(n2)	O(n*log2n)	不一顶	O(n)
插入排序	O(n2)	O(n2)	稳定	O(1)
堆排序	O(n*log2n)	O(n*log2n)	不稳定	O(1)
希尔排序	O	O	不稳定	O(1)

类似于时间复杂度的讨论，一个算法的空间复杂度(Space Complexity)S(n)定义为该算法所耗费的存储空间，它也是问题规模n的函数。渐近空间复杂度也常常简称为空间复杂度。 

• 空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。一个算法在计算机存储器上所占用的存储空间，包括存储算法本身所占用的存储空间，算法的输入输出数据所占用的存储空间和算法在运行过程中临时占用的存储空间这三个方面。

我们在写代码时，完全可以用空间来换取时间，比如说，要判断某某年是不是闰年，你可能会花一点心思写了一个算法，而且由于是一个算法，也就意味着，每次给一个年份，都是要通过计算得到是否是闰年的结果。还有另一个办法就是，事先建立一个有2 050个元素的数组（年数略比现实多一点），然后把所有的年份按下标的数字对应，如果是闰年，此数组项的值就是1，如果不是值为0。这样，所谓的判断某一年是否是闰年，就变成了查找这个数组的某一项的值是多少的问题。此时，我们的运算是最小化了，但是硬盘上或者内存中需要存储这2050个0和1。

算法的输入输出数据所占用的存储空间是由要解决的问题决定的，是通过参数表由调用函数传递而来的，它不随本算法的不同而改变。存储算法本身所占用的存储空间与算法书写的长短成正比，要压缩这方面的存储空间，就必须编写出较短的算法。算法在运行过程中临时占用的存储空间随算法的不同而异，有的算法只需要占用少量的临时工作单元，而且不随问题规模的大小而改变，我们称这种算法是“就地"进行的，是节省存储的算法，如这一节介绍过的几个算法都是如此；有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如将快速排序和归并排序算法就属于这种情况。

通过一笔空间上的开销来换取计算时间的小技巧。到底哪一个好，其实要看你用在什么地方。

算法的空间复杂度通过计算算法所需的存储空间实现，算法空间复杂度的计算公式记作：S(n)= O(f(n))，其中，n为问题的规模，f(n)为语句关于n所占存储空间的函数。

一般情况下，一个程序在机器上执行时，除了需要存储程序本身的指令、常数、变量和输入数据外，还需要存储对数据操作的存储单元。若输入数据所占空间只取决于问题本身，和算法无关，这样只需要分析该算法在实现时所需的辅助单元即可。若算法执行时所需的辅助空间相对于输入数据量而言是个常数，则称此算法为原地工作，空间复杂度为O(1)。

• 关于O(1)的问题， O(1)是说数据规模和临时变量数目无关，并不是说仅仅定义一个临时变量。举例：无论数据规模多大，我都定义100个变量，这就叫做数据规模和临时变量数目无关。就是说空间复杂度是O(1)。
• 那就是指函数运行时处理数据的规模与空间和时间的一个变化时的比例关系，不是具体的数值。

当一个算法的空间复杂度为一个常量，即不随被处理数据量n的大小而改变时，可表示为O(1)；当一个算法的空间复杂度与以2为底的n的对数成正比时，可表示为0(10g2n)；当一个算法的空I司复杂度与n成线性比例关系时，可表示为0(n).若形参为数组，则只需要为它分配一个存储由实参传送来的一个地址指针的空间，即一个机器字长空间；若形参为引用方式，则也只需要为其分配存储一个地址的空间，用它来存储对应实参变量的地址，以便由系统自动引用实参变量。 

• 通常，我们都使用“时间复杂度”来指运行时间的需求，使用“空间复杂度”指空间需求。当不用限定词地使用“复杂度”时，通常都是指时间复杂度。

对于一个算法，其时间复杂度和空间复杂度往往是相互影响的。当追求一个较好的时间复杂度时，可能会使空间复杂度的性能变差，即可能导致占用较多的存储空间；反之，求一个较好的空间复杂度时，可能会使时间复杂度的性能变差，即可能导致占用较长的运行时间。另外，算法的所有性能之间都存在着或多或少的相互影响。因此，当设计一个算法(特别是大型算法)时，要综合考虑算法的各项性能，算法的使用频率，算法处理的数据量的大小，算法描述语言的特性，算法运行的机器系统环境等各方面因素，才能够设计出比较好的算法。