二分图最大匹配问题与匈牙利算法的核心思想

最近在学习图论相关知识，读到二分图最大匹配问题的匈牙利算法，感觉很有意思，所以记录下来。

概念

在假设读者已经了解图论最最基本的概念的基础上（例如：顶点、边、路径、圈），我们先来看一下二分图特有的概念定义。

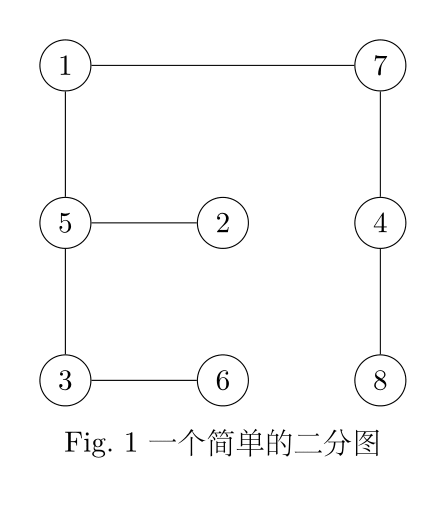
二分图（Bigraph, Bipartite graph）是一种特殊的图，它的顶点可以被分成两个不相交的集合（ U U 和  V V），并且同属一个集合内的点两两不相连（ EU=EV=∅ EU=EV=∅）。这也就是说，如果一个图是二分图，那么它要么没有圈，要么圈所包含的边的数量必定是偶数。

Fig. 1 是一个简单的二分图

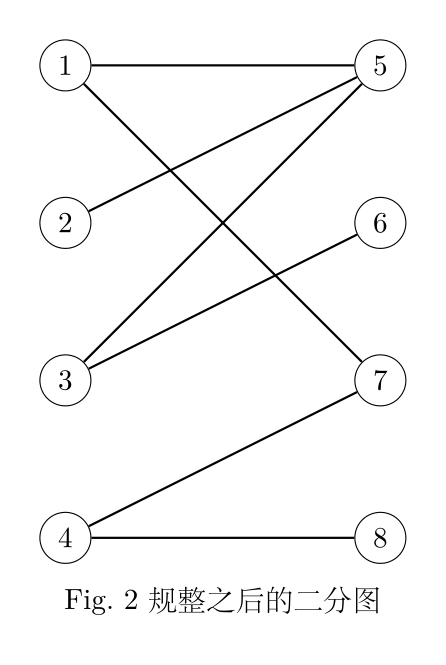
为了方便观看我们通常将它画为 Fig. 2 的形式：

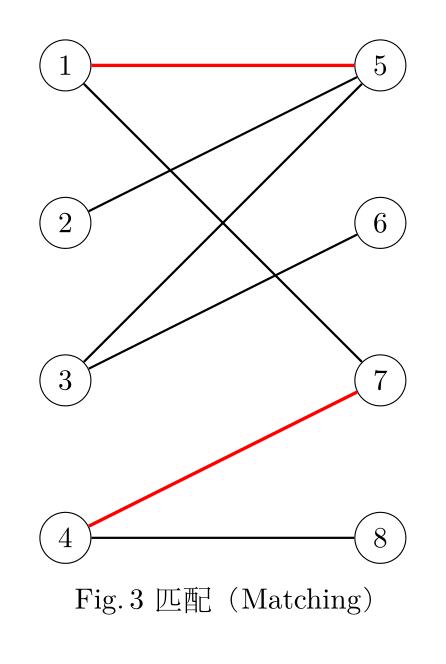
匹配（Matching）是边的集合（ M⊂E M⊂E），其中任意两条边不共点（ ∀e1,e2∈M s.t. e1∩e2=∅ ∀e1,e2∈M s.t. e1∩e2=∅）。Fig. 3 中标红的边组成的集合，就是一个匹配。这些标红的边，被称为匹配边；匹配边所连接的点则被称为匹配点。同理可以定义非匹配边和非匹配点的概念。

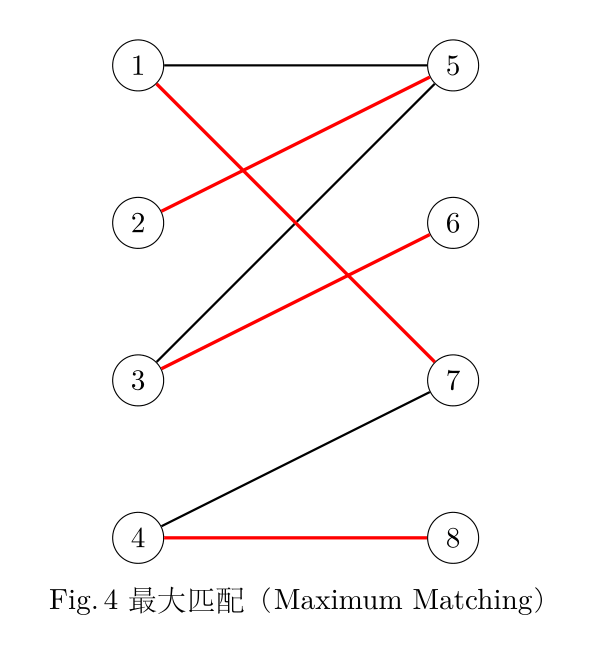
显而易见，对于一个二分图来说，可能有很多种匹配。如果二分图里的某一个匹配包含的边的数量，在该二分图的所有匹配中最大，那么这个匹配称为最大匹配（Maximum Matching）。Fig. 4 是最大匹配的示例。

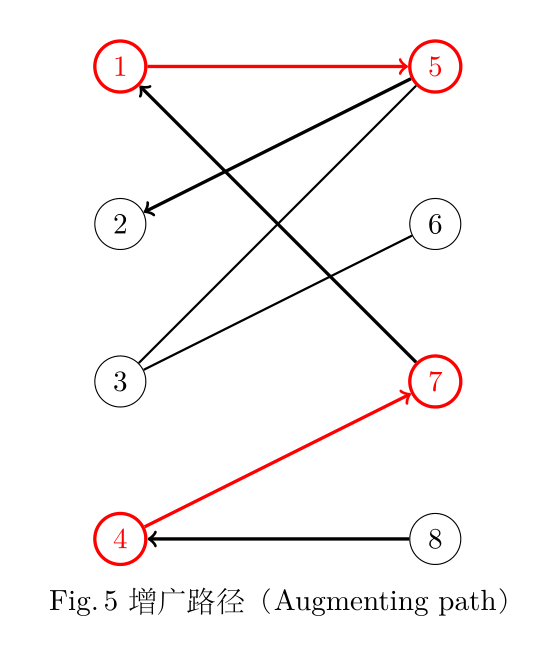
在二分图的匹配中，如果一条路径的首尾是非匹配点，路径中除此之外（如果有）其他的点均是匹配点，那么这条路径就是一条增广路径（Agumenting path）。Fig. 5 中，粗红线标出的是匹配路径和匹配点。

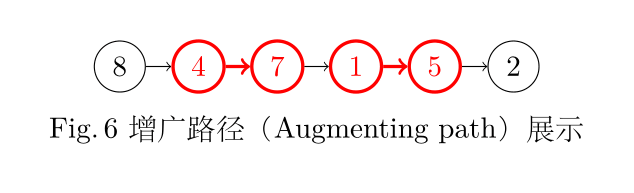
显而易见，8->4->7->1->5->2 是一条增广路径。因为 8 和 2 作为路径的首尾是非匹配点，而路径中剩余的 4/7/1/5 均是匹配点。

匈牙利算法

增广路径的首尾是非匹配点。因此，增广路径的第一条和最后一条边，必然是非匹配边；同时它的第二条边（如果有）和倒数第二条边（如果有），必然是匹配边；以及第三条边（如果有）和倒数第三条边（如果有），一定是非匹配边。

亦即，增广路径从非匹配边开始，匹配边和非匹配边依次交替，最后由非匹配边结束。这样一来，增广路径中非匹配边的数目会比匹配边大 1。

如果我们置换增广路径中的匹配边和非匹配边，由于增广路径的首尾是非匹配点，其余则是匹配点，这样的置换不会影响原匹配中其他的匹配边和匹配点，因而不会破坏匹配；亦即增广路径的置换，可以得到比原有匹配更大的匹配（具体来说，匹配的边数增加了 1）。

由于二分图的最大匹配必然存在（比如，上限是包含所有顶点的完全匹配），所以，再任意匹配的基础上，如果我们有办法不断地搜寻出增广路径，直到最终我们找不到新的增广路径为止，我们就有可能得到二分图的一个最大匹配。这就是匈牙利算法的核心思想。

唯一的问题在于，在这种贪心的思路下，我们如何保证不存在例外的情况，即：当前匹配不是二分图的最大匹配，但已找不到一条新的增广路径。

我们从反证法考虑，即假设存在这样的情况。因为当前匹配不是二分图的最大匹配，那么在两个集合中，分别至少存在一个非匹配点。那么情况分为两种：

1. 这两个点之间存在一条边——那么我们找到了一条新的增广路径，产生矛盾；
2. 这两个点之间不存在直接的边，即这两个点分别都只与匹配点相连——那么：
   1. 如果这两个点可以用已有的匹配点相连，那么我们找到了一条新的增广路径，产生矛盾；
   2. 如果这两个点无法用已有的匹配点相连，那么这两个点也就无法增加匹配中边的数量，也就是我们已经找到了二分图的最大匹配，产生矛盾。

在所有可能的情况，上述假设都会产生矛盾。因此假设不成立，亦即贪心算法必然能求得最大匹配的解。