拉格朗日中值定理
如果函数f(x)满足
那么在(a,b)内至少有一点ξ(a < ξ < b),使等式
成立。此定理称为拉格朗日中值定理。拉格朗日中值定理是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形。
积分中值定理
积分中值定理分为积分第一中值定理和积分第二中值定理,它们各包含两个公式。其退化状态均指在ξ的变化过程中存在一个时刻使两个图形的面积相等(严格表述在下面)。
积分第一中值定理
设 ![f:[a,b]\rightarrow \mathbf R](http://upload.wikimedia.org/wikipedia/zh/math/9/b/a/9ba825fa54d53e3f4614429fd3932aa6.png) 为一连续函数,
为一连续函数,![g:[a,b]\rightarrow \mathbf R](http://upload.wikimedia.org/wikipedia/zh/math/4/d/7/4d71fc0f690cd89ed8b0d4ece8885c71.png) 为一正的可积函数,那么存在一点
为一正的可积函数,那么存在一点 ![\xi\in [a,b]](http://upload.wikimedia.org/wikipedia/zh/math/f/8/3/f83ba3f626ed0ec9d1df2f3139d398d0.png) 使得
使得
-
 。
。
证明
因为 f 是闭区间上的连续函数,f 取得最大值 M 和最小值 m。于是
-
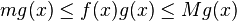 。
。
对不等式求积分,我们有
-
 。
。
若  ,则
,则 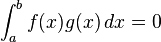 。ξ 可取 [a,b] 上任一点。
。ξ 可取 [a,b] 上任一点。
设 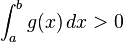 ,那么
,那么
-
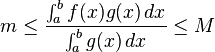 。
。
因为  是连续函数,则必存在一点
是连续函数,则必存在一点 ![\xi\in [a,b]](http://upload.wikimedia.org/wikipedia/zh/math/f/8/3/f83ba3f626ed0ec9d1df2f3139d398d0.png) ,使得
,使得
-
 。
。
推论(拉格朗日中值定理的积分形式)
在上式中令g(x) = 1,则可得出:
设 ![f:[a,b]\rightarrow \mathbf R](http://upload.wikimedia.org/wikipedia/zh/math/9/b/a/9ba825fa54d53e3f4614429fd3932aa6.png) 为一连续函数,则∃
为一连续函数,则∃![\xi \in [a,b]](http://upload.wikimedia.org/wikipedia/zh/math/f/8/3/f83ba3f626ed0ec9d1df2f3139d398d0.png) ,使
,使
它也可以由拉格朗日中值定理推出:
设F(x)在[a,b]上可导,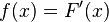 ,则∃
,则∃![\xi \in [a,b]](http://upload.wikimedia.org/wikipedia/zh/math/f/8/3/f83ba3f626ed0ec9d1df2f3139d398d0.png) ,使
,使
积分第二中值定理
积分第二中值定理与积分第一中值定理相互独立,却又是更精细的积分中值定理。它可以用来证明Dirichlet-Abel 反常 Rieman 积分判别法。
内容
若f,g在[a,b]上黎曼可积且f(x)在[a,b]上单调,则存在[a,b]上的点ξ使
-
 ;
;
退化态的几何意义
令g(x)=1,则原公式可化为:
-
 ;
;
进而导出:









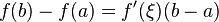



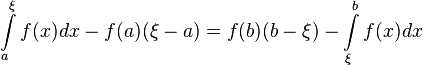













 12万+
12万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








