6 动态规划
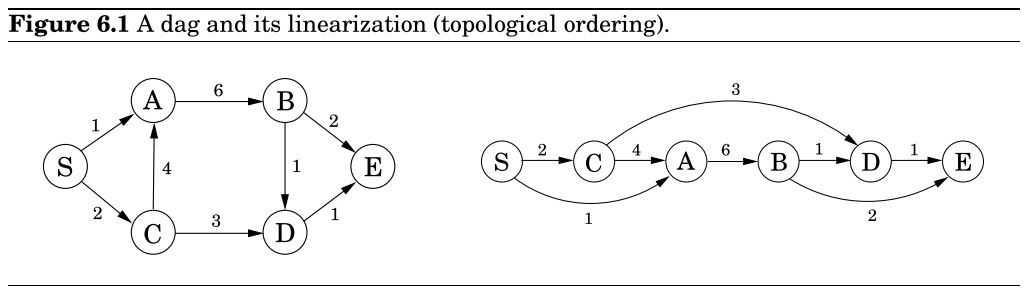
6.1 重新审视DAG的最短路径问题
- 有向无环图DAG的节点可以被线性化:
procedure dag-shortest-paths(G,l,s)
Input: Graph G=(V,E), dag;
edge lengths {le:e ∈ E};
vertex s ∈ V
Output: For all vertices u reachable from s,dist(u) is set
to the distance from s to u.
for all u ∈ V
dist(u)= ∞
dist(s)=0
Linearize G //通过深度优先搜索线性化(拓扑排序)
for each u ∈ V in Linearized order:
for all edges (u,v) ∈ E:
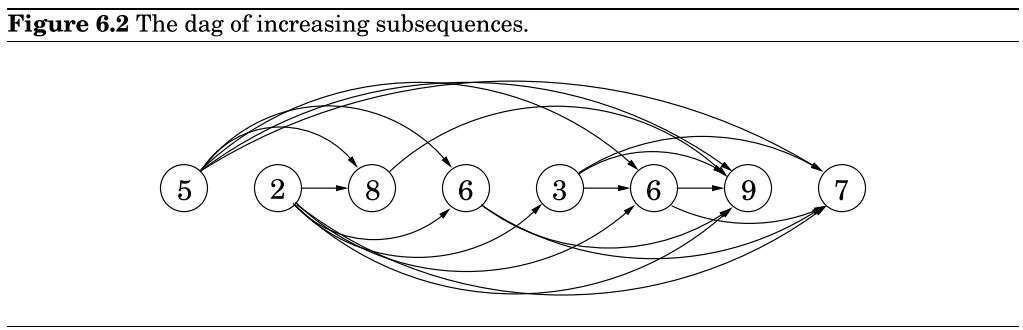
dist(v)=min(dist(u)+l(u,v))6.2 最长递增子序列
for j=1,2,...,n
L(j)=1+max{L(i):(i,j) ∈ E}
return L
//i为j的前驱,求反转图Gr即可6.3 编辑距离
将两个单词进行对齐,对齐代价为对应字母不相同的列数
6.3.1 一种动态规划的解
寻找两个字串: x[1...m],y[1...n] 之间的编辑距离 E(m,n) ,考虑字符串的前缀: x[1...i],y[1...j] 的编辑距离 E(i,j) 。
则:
E(i,j)=min{1+E(i−1,j),1+E(i,j−1),diff(i,j)+E(i−1,j−1)}
for i=0,...,m:
E(i,0)=i
for j=0,...,n:
E(0,j)=j
for i=1,...,m:
for j=1,...,n:
E(i,j)=min{1+E(i-1,j),1+E(i,j-1),diff(i,j)+E(i-1,j-1)}
return E6.3.2 隐含的dag
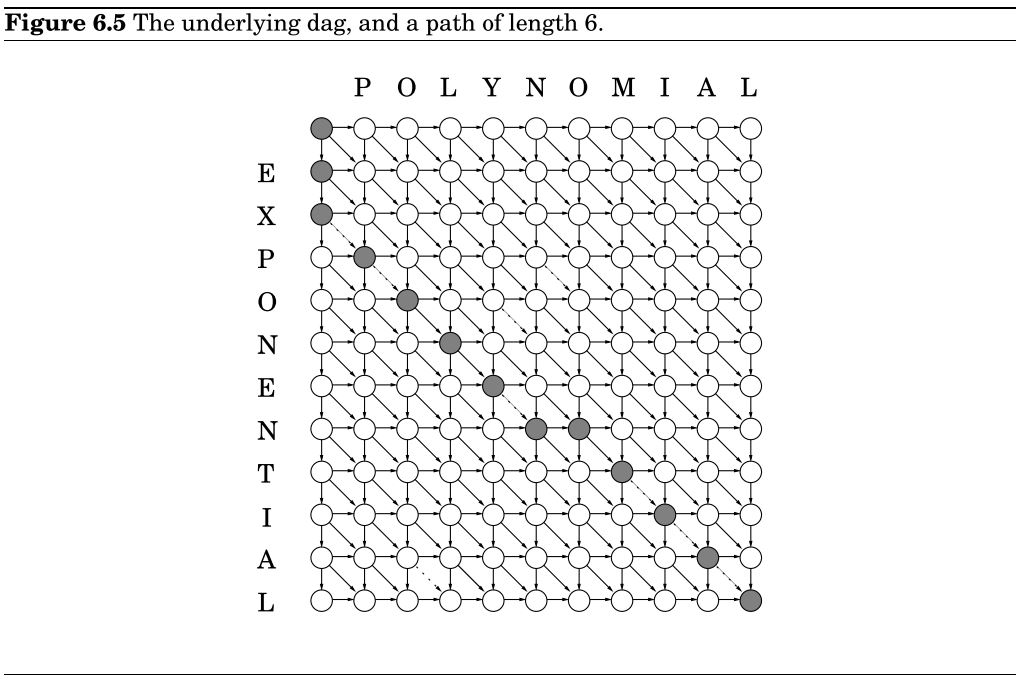
每个动态规划都隐含着一个dag结构:每个节点表示一个子问题,每条边表示解决子问题时的先后约束。
除边 {(i−1,j−1)→(i,j):x[i]=y[j]} 为0外,其余边为0;问题转为求点 s=(0,0) 到点 t=(m,n) 的最短距离。
其中,为使 EXPONENTIAL 转为 POLYNOMIAL
- 向下表示删除
- 向右表示插入
向对角线表示匹配或替换
6.4 背包问题
- n件物品,W总重量的背包,复杂度 O(nW)
6.4.1 多副本背包问题
- Knapsack with repetition
定义K(w)=容量w可以容纳的最高价值,则:K(w)=maxi:wi≤w{K(w−wi)+vi}
K(0)=0
for w=1 to W
K(w)=max{K(w-w_i)+v_i:w_i≤w}
return K(W)6.4.2 单副本背包问题
- Knapsack without repetition
定义K(w,j)=基于容量w、1...j个物品可以容纳的最高价值,则:K(w)=max{K(w−wi,j−1)+vi,K(w,j−1)}
for j=1...n:
K(0,j)=0
for w=1...W:
K(w,0)=0
for j=1...n:
for w=1...W:
if w_j > w:
K(w,j)=K(w,j-1)
else:
K(w,j)=max{K(w,j-1),K(w-w_j,j-1)+v_j}
return K(W,n)6.5 矩阵链式相乘
- 矩阵A[m0,m1]与A[m1,m2]相乘的复杂度为O(m0∗m1∗m2)
- 求n个矩阵相乘: A1∗A2∗...∗An
定义C(i,j)=计算Ai∗Ai+1∗...∗Aj的最小代价,则:C(i,j)=mini≤k<j{C(i,k)+C(k+1,j)+mi−1∗mk∗mj}
for i=1...n:
C(i,i)=0
for s=1...n-1:
for i=1...n-s:
j=i+s
C(i,j)=min{C(i,k)+C(k+1,j)+m(i-1)*m(k)*m(j):i≤k<j}
return C(1,n)6.6 最短路径问题
6.6.1 最短可靠路径
- 求s到t最多经过k条边的最短路径
定义dist(v,i)=s到v经过i条边的最短路径dist(v,i)=min(u,v)∈E{dist(u,i−1)+l(u,v)}
6.6.2 所有顶点间的最短路径
- 包含负边的s源点最短路径算法复杂度 O(|V|∗|E|) ;对每一个顶点进行遍历,则复杂度为 O(|V|2∗|E|)
- 基于动态规划的Floyd-Warshall算法,复杂度为 O(|V|3)
定义shortestPath(i,j,k)=使用{1,...,k}为中间节点时,i到j的最短路径shortestPath(i,j,k+1)=min(shortestPath(i,j,k),shortestPath(i,k+1,k)+shortestPath(k+1,j,k))
let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
for each vertex v
dist[v][v] ← 0
for each edge (u,v)
dist[u][v] ← w(u,v) // the weight of the edge (u,v)
for k from 1 to |V|
for i from 1 to |V|
for j from 1 to |V|
if dist[i][j] > dist[i][k] + dist[k][j]
dist[i][j] ← dist[i][k] + dist[k][j]
end if6.6.3 旅行商问题TSP
- 对于包含城市1的子集 S⊂{1,2,...,n} ,以及 j∈S ,令 C(S,j) 为由1出发、终点为j的经过s所有节点恰好一次的最短路径长度。 O(n22n)
C(S,j)=mini∈S:i≠j{C(S−{j})+dij}
function algorithm TSP (G, n)
for k := 2 to n do
C({1, k}, k) := d(1,k)
end for
for s := 3 to n do
for all S ⊆ {1, 2, . . . , n}, |S| = s do
for all k ∈ S do
{C(S, k) = min_{m≠1,m≠k,m∈S} [C(S − {k}, m) + d(m,k) ]}
end for
end for
end for
opt := min_{k≠1} [C({1, 2, 3, . . . , n}, k) + d(k,1)]
return (opt)
end6.7 树中的独立集
- 选定树中任意节点r为树根,子问题:
I(u)=u下子树的最大独立集规模I(u)=max{1+∑w为u孩子的孩子I(w),∑w为u的孩子I(w)}








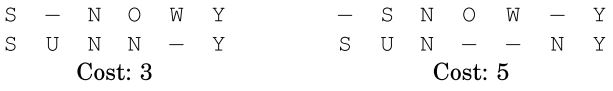
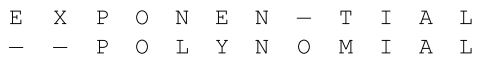













 638
638











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








