二叉树的简单应用--表达式树

表达式树

算数表达式是分层的递归结构，一个运算符作用于相应的运算对象，其运算对象又可以是任意复杂的表达式。二叉树的递归结构正好用来表示这种表达式。下面只讨论二元表达式。
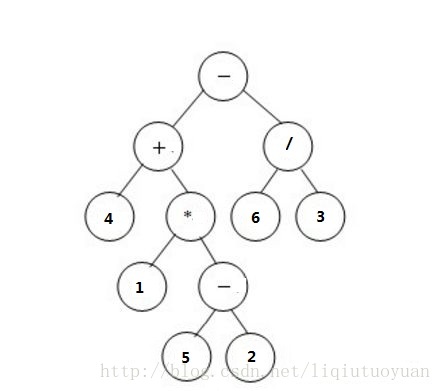
二元表达式可以很自然的联系到二叉树：以基本运算对象作为叶节点中的数据；以运算符作为非叶节点中的数据，其两棵子树是它的运算对象，子树可以是基本运算对象，也可以是复杂表达式。如图是一个表达式树。

前缀、中缀和后缀表达式

中缀表达式（中缀记法）
我们平时缩写的表达式，将运算符写在两个操作数中间的表达式，称作中缀表达式。在中缀表达式中，运算符有不同的优先级，圆括号用于改变运算顺序，这使得运算规则比较复杂，求值过程不能直接从左到右顺序进行，不利于计算机处理。

后缀表达式
将运算符写在两个操作数之后的表达式称作后缀表达式。后缀表达式中没有括号，从而运算符没有优先级。后缀表达式的求值过程能够严格按照从左到右的顺序进行，有利于计算机处理。

前缀表达式
前缀表达式是将运算符写在两个操作数之前的表达式。和后缀表达式一样，前缀表达式没有括号，运算符没有优先级，能严格按照从右到左的顺序计算。

另外，算式表达式和表达式树的关系如下：

• 表达式树的先根遍历：前缀表达式
• 表达式树的中根遍历：中缀表达式
• 表达式树的后根遍历：后缀表达式

表达式的转换

利用表达式树

给定一个表达式的中缀形式：(4+1*(5-2))-6/3
首先将每个运算加上括号，区分优先级，得到(4+(1*(5-2)))-(6/3)
括号外的-优先级最低，作为根节点，(4+(1*(5-2)))作为左子树，(6/3)作为右子树；
递归的转换4+(1*(5-2))，+最为根节点，4是左子树，(1*(5-2))是右子树。*是右子树的根节点，1是左子树，(5-2)是右子树。最后计算(5-2)，-是根节点，5是左子树，2是右子树。得到的表达式树如上图。

构造好表达式树之后，前缀表达式和中缀表达式可根据先根遍历和后根遍历得到。
前缀表达式：- + 4 * 1 - 5 2 / 6 3
后缀表达式：4 1 5 2 - * + 6 3 / -

利用栈

将中缀表达式转换为后缀表达式
step1：初始化一个栈和一个后缀表达式字符串
step2：从左到右依次对中缀表达式中的每个字符进行以下处理，直到表达式结束

• 如果字符是‘（’，将其入栈
• 如果字符是数字，添加到后缀表达式的字符串中
• 如果字符是运算符，先将栈顶优先级不低于该运算符的运算符出栈，添加到后缀表达式中，再将该运算符入栈。当‘（’在栈中是，优先级最低
• 如果字符是‘）’，将栈顶元素出栈，添加到后缀表达式中，直到出栈的是‘（’
  step3：如果表达式结束，但栈中还有元素，将所有元素出栈，添加到后缀表达式中

例如给定一个表达式的中缀形式：(4+1*(5-2))-6/3，栈中和表达式的变化如下表所示：
|扫描到的元素|栈|后缀表达式|说明|

扫描到的元素	栈	后缀表达式	说明
(	(		将(入栈，表达式空
4	(	4	将4加入表达式
+	( +	4	将+入栈
1	( +	4 1	将1加入表达式
*	( + *	4 1	将*入栈
(	( + * (	4 1	将(入栈
5	( + * (	4 1 5	将5加入表达式
-	( + * ( -	4 1 5	将-入栈
2	( + * ( -	4 1 5 2	将2 加入表达式
)	( + *	4 1 5 2 -	-出栈，加入表达式
)		4 1 5 2 - * +	*和+出栈，加入表达式，栈空
-	-	4 1 5 2 - * +	-入栈
6	-	4 1 5 2 - * + 6	6加入表达式
/	-/	4 1 5 2 - * + 6	/入栈
3	-/	4 1 5 2 - * + 6 3	3加入表达式
		4 1 5 2 - * + 6 3 / -	表达式扫描结束，将栈中元素加入表达式

最后得到后缀表达式为4 1 5 2 - * + 6 3 / -

将中缀表达式转换为前缀表达式
中缀表达式转换到前缀表达的方法和转换到后缀表达式过程一致，细节上有所变化
step1：初始化两个栈s1 和s2
step2：从右到左依次对中缀表达式中的每个字符进行以下处理，直到表达式结束

• 如果字符是‘)’，将其入栈
• 如果字符是数字，添加到s2中
• 如果字符是运算符，先将栈顶优先级不低于该运算符的运算符出栈，添加到s2中，再将该运算符入栈。当‘）’在栈中是，优先级最低
• 如果字符是‘（’，将栈顶元素出栈，添加到s2中，直到出栈的是‘）’
  step3：如果表达式结束，但栈中还有元素，将所有元素出栈，添加s2中
  step4：将栈s2中元素依次出栈，即得到前缀表达式

给定一个表达式的中缀形式：(4+1*(5-2))-6/3，其前缀形式为 - + 4 * 1 - 5 2 / 6 3

表达式的计算

中缀表达式的计算我们已经非常清楚，前缀和后缀表达式更适合计算机处理
后缀表达式的计算
后缀表达式没有括号，运算符的顺序即为实际运算顺序，在求值过程中，当遇到运算符时，只要取得前两个操作数就可以立即进行计算。当操作数出现时，不能立即求值，需要先保存等待运算符。对于等待中的操作数而言，后出现的先运算，所以需要一个栈辅助操作。
后缀表达式的运算过程如下：
step1：设置一个栈
step2：从左到右对后缀表达式中的字符进行以下处理：
- 如果字符是数字，现将其转化为数字，然后入栈
- 如果字符是运算符，出栈两个值进行计算。计算结果入栈
- 重复以上步骤，直到后缀表达式扫描结束，栈中最后一个元素就是表达式的结果。

给定后缀表达式4 1 5 2 - * + 6 3 / -，依次将4 1 5 2 入栈，当扫描到-时，2,5出栈，计算5-2=3；将3入栈，此时栈中元素为4 1 3。接着扫描到*，3 1出栈，计算1*3=3,3入栈，栈中元素为4 3,。扫描+，3 4出栈，计算4+3=7,7入栈。接着6 3 入栈，栈中该元素为7 6 3，扫描到/，3 6出栈，计算6/3=2,2入栈，栈中元素为7 2.扫描-，2 7 出栈，计算7-2=5,5入栈。表达式扫描完毕，栈中元素为5，表达式结果为5.
前缀表达式的计算
前缀表达式的计算扫描顺序从右到左，其他和后缀表达式的计算完全一致。