DirectX学习笔记（十三）：取景变换矩阵计算及3D世界摄像机的原理分析和实现

前言：

在玩3D游戏中，我们对于整个游戏场景的视野获取就是通过摄像机来完成的。由此可见摄像机的重要性。前面的所有例子都是针对于摄像机固定来说的。这一次我们来设计一个摄像机（模拟游戏场景中的摄像机）。

取景变换计算过程：

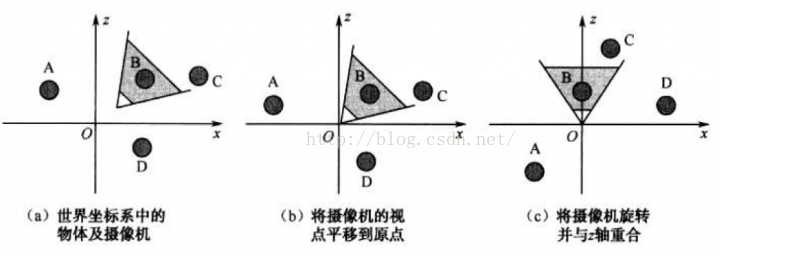
在前面我们讲过取景变换。在当摄像机的位置和朝向任意时，进行一些操作会造成效率低下很是麻烦。为了简化运算，我们将摄像机变换到世界坐标系的原点，并旋转摄像机使其光轴与世界坐标系的z轴正方向朝向一致。要特别注意的是，世界中的所有物体都会随之摄像机变换，以保证摄像机的视场恒定。

如下图：

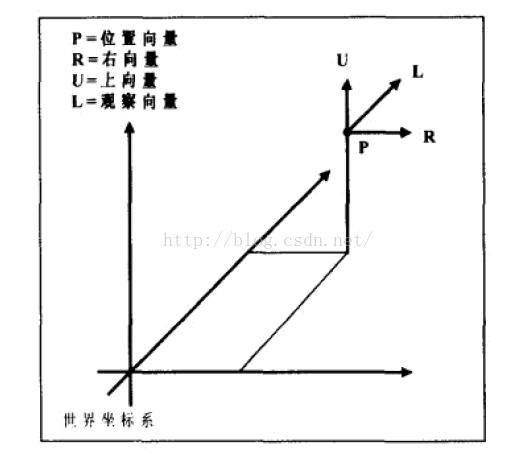
由此可见，我们要描述一个摄像机必须有四个向量：右向量（right）、上向量（up）、观察向量（look）、位置向量（position）。实际上，这些向量的定义意味着我们定义了一个局部的坐标系。

这样，我们就可以通过这四个向量来进行以下变换：

绕向量right的旋转

绕向量up的旋转

绕向量look的旋转

沿向量right方向的扫视

沿向量up的升降

沿向量look的平动

如下图所示：

那么，我们怎么才能实现这些变换呢？答案：通过矩阵运算！！

 
为了讲解方便，我们令向量

                                 p = （px,py,pz)表示位置向量，position
    r = (rx,ry,rz) 向量表示右向量， right
         u = (ux,uy,uz)  向量表示上向量，up
<