Java常用算法——迭代 & 递归篇

迭代 & 递归

迭代

(1).定义

来自维基百科:

迭代是重复反馈过程的活动，其目的通常是为了接近并到达所需的目标或结果。每一次对过程的重复被称为一次”迭代”，而每一次迭代得到的结果会被用来作为下一次迭代的初始值。

在数学中:
数学中的迭代可以指函数迭代的过程，即反复地运用同一函数计算，前一次迭代得到的结果被用于作为下一次迭代的输入。即使是看上去很简单的函数，在经过迭代之后也可能产生复杂的行为，衍生出具有难度的问题。这样的例子可以参见考拉兹猜想和杂耍者序列（Juggler sequence）。又如一个简单的二次变换x→x(1-x)，它的迭代将形成一个具有混沌性质的动力系统。
迭代在数学中的另一应用是迭代法，用来对特定数学问题作数值解估计。牛顿法就是迭代法的一个例子。

在计算机中:
在计算机科学中，迭代是程序中对一组指令（或一定步骤）的重复。它既可以被用作通用的术语（与”重复”同义），也可以用来描述一种特定形式的具有可变状态的重复。
在第一种意义下，递归是迭代的一个例子，但是通常使用一种递归式的表达。比如用0!=1，n!=n\*(n-1)!来表示阶乘。而迭代通常不是这样写的。
而在第二种（更严格的）意义下，迭代描述了在指令式编程语言中使用的编程风格。与之形成对比的是递归，它更偏向于声明式的风格。

这里是一个依赖于破坏性赋值的迭代的例子，以指令式的虚拟码写成：

 var i, a = 0        // 迭代前初始化
 for i from 1 to 3    // 循环3次
 {  
     a = a + i       // a的值增加i
 }
 print a              // 打印出数字6

在这个程序片段中，变量i的值会不断改变，依次取值1、2和3。这种改变赋值——或者叫做可变状态——是迭代的特征。

(2).示例

迭代的概念不难理解，下面是一个迭代的小例子

牛顿迭代法：

设r是$f(x)=0$的根，选取$x_0$作为r的初始近似值，过点($x_0$，$f(x_0)$)做曲线$y=f(x)$的切线L，L的方程为$y = f(x_0) + f^\prime(x_0)(x-x_0)$，求出L与x轴交点的横坐标$x_1 = x_0 - \frac{f(x_0)}{f^\prime(x_0)}$ ，称$x_1$为r的一次近似值。过点($x_1$，$f(x_1)$)做曲线$y=f(x)$的切线，并求该切线与x轴交点的横坐标$x_2 = x_1 - \frac{f(x_1)}{f^\prime(x_1)}$，称$x_1$为r的二次近似值。重复以上过程，得r的近似值序列，其中，$x_{n+1} = x_n - \frac{f(x_n)}{f^\prime(x_n)}$ 称为r的 n+1次近似值，上式称为牛顿迭代公式。

用牛顿迭代法解非线性方程，是把非线性方程$f(x)=0$线性化的一种近似方法。把$f(x)$在点$x_0$的某邻域内展开成泰勒级数:

$$f(x) = f(x_0) + f^\prime(x_0)(x-x_0) + \frac{f^{\prime\prime}(x_0)(x-x_0)^2}{2!} + ... + \frac{f^{(n)}(x_0)(x-x_0)^n}{n!} + R_n(x)$$
取其线性部分（即泰勒展开的前两项），并令其等于0，即 $f(x_0) + f^\prime(x_0)(x-x_0) = 0$，以此作为非线性方程 $f(x) = 0$的近似方程，若 $f^\prime(x_0)≠0$ ，则其解为 $x_1 = x_0 - \frac{f(x_0)}{f^\prime(x_0)}$。
这样，得到牛顿迭代法的一个迭代关系式： $x_{n+1} = x_n - \frac{f(x_n)}{f^\prime(x_n)}$。

图示:

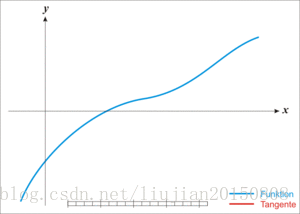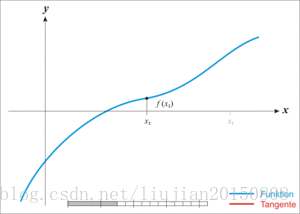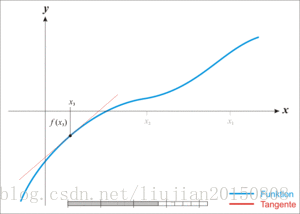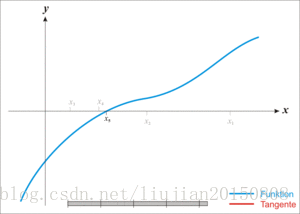
因此，有了以上的知识预备之后，我们就可以利用牛顿迭代法求算术平方根了。即求$x^2 - a = 0$的正根。
则令$f(x) = x^2 - a$因此$f(x)$求一阶导的结果为:
　　　　　　

$$f^\prime(x) = 2x$$
而牛顿迭代式为：
　　　　　　 $$x_{n+1} = x_n - \frac{x_n^2 - a}{2x_n} = {1 \over 2}(x_n + {a \over x_n})$$
因此可以任意指定一个迭代的初始值，例如 $x_0 = 1$，代入上面的式子迭代。
例如计算 $\sqrt{2}$，即此时 a=2。
$x_0 = 1$
$x_1 = {1 \over 2}(1 + {2 \over 1}) = 1.5$
$x_2 = {1 \over 2}(1.5 + {2 \over 1.5}) = 1.4166...$
$...$
因此我们在计算的时候可以设置一个迭代终止条件，即设置精度，这样的话得到的结果即是精度范围内的近似结果，可用如下方式设置精度：
$${(x * x - a) \over a }<= 指定的精度(如1e-6等)$$
因此当误差小于指定精度时，则停止迭代。
小例子:

package month12.day12;

import java.util.Scanner;

/**
 * Created by Administrator on 2016/12/12.
 */
public class TestForSqrt {
    public static void main(String args[]) {
        Scanner scanner = new Scanner(System.in);
        while(scanner.hasNextInt()) {
            int number = scanner.nextInt();
            double x = 1;
            do {
                x = 0.5 * (x + number / x);
            }while ((x * x - number) / number > 1e-6);
            System.out.println("The NewTon Method solve:" + number + "\'s sqrt is:" + x);
            System.out.println("The Math class's static method solve: " + number + "\'s sqrt is:" + Math.sqrt(number)); //number自动类型提升至double传入sqrt()方法
        }
    }
}

延伸:【用牛顿迭代法开任意次方】

求$\sqrt[k]{a}$的递推式为:
　　　　　　

$$x_{n+1} = x_n - \frac{x_n^k - a}{kx_n^{k-1}} = {{k-1} \over k}x_n + {a \over {kx_n^{k-1}}}$$

递归

(1).定义

来自维基百科:

递归（英语：recursion）在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。

[1] 递归式方法可以被用于解决很多的计算机科学问题，因此它是计算机科学中十分重要的一个概念。

[2] 绝大多数编程语言支持函数的自调用，在这些语言中函数可以通过调用自身来进行递归。计算理论可以证明递归的作用可以完全替换循环，因此在很多函数编程语言（如Scheme）中习惯用递归来实现循环。

(2).示例

1.阶乘问题

对于阶乘问题，显然可以给出如下定义：

$$n! = \begin{cases} 1 &\mbox{if n = 0}\\ n*(n-1)! &\mbox{if n $\geq$ 1 } \end{cases}$$
这样的话，就将一个 n阶问题转化成了一个 n-1阶的问题。而问题的”出口”即为 n == 0时，当问题分解至 n == 0，则可将子问题的结果一层一层迭代回其原问题，直至得出最后的结果返回主函数。示例代码:

package month12.day12;

import java.util.Scanner;

/**
 * Created by Administrator on 2016/12/12.
 */
public class TestForFac {
    public static void main(String args[]) {
        Scanner scanner = new Scanner(System.in);
        while (scanner.hasNextLong()) {
            long number = scanner.nextLong();
            System.out.println(number + "! = " + fac(number));
        }
    }
    static long fac(long num) {
        if (num == 0) {
            return 1;
        } else {
            return num * fac(num - 1);
        }
    }
}

程序运行结果:

4
4! = 24
3
3! = 6
5
5! = 120
0
0! = 1

另外可以模拟递归分解问题以及迭代回原问题的过程，加深对递归的理解，如下:

#include <stdio.h>

int Fib(int n, int step) {
    if (n == 1) {
        return 1;
    } else {
        int temp = step;
        while (temp--) {
            printf("  ");
        }
        printf("%dx%d!\n", n, n - 1);
        int value = Fib(n - 1, step + 1);
        temp = step;
        while (temp--) {
            printf("  ");
        }
        printf("%dx%d\n", n, value);
        return n * value;
    }
}

int main() {
    int n;
    while (scanf("%d", &n) != EOF) {
        printf("%d\n", Fib(n, 0));
    }
    return 0;
}

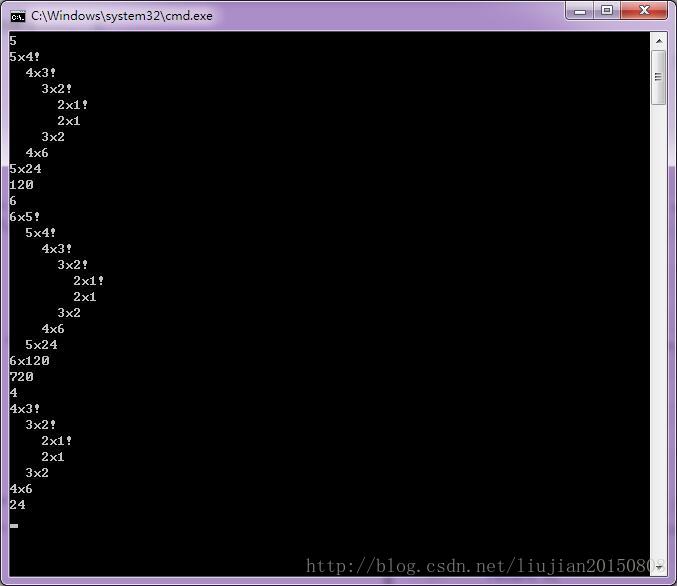
程序运行结果:

2.汉诺塔问题

汉诺塔是根据一个传说形成的数学问题：
有三根杆子A，B，C。A杆上有N个(N>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆：
　　　　每次只能移动一个圆盘；
　　　　大盘不能叠在小盘上面。
提示：可将圆盘临时置于B杆，也可将从A杆移出的圆盘重新移回A杆，但都必须遵循上述两条规则。
问：如何移？最少要移动多少次？

根据问题提示，很容易想到，我在移动n个圆盘的时候，由于大盘不能叠在小盘上面，所以我肯定想怎么样能先把最后一个盘子移到C杆去，这样的话就不用再管最大的那个盘子了。那么顺着这样的思路，我要把最后一个盘子移到C杆去，那这最后一个大盘子上的n-1个盘子要先移开才行。这n-1个盘子移开之后，然后我就可以把最后一个盘子（也就是最大的那个）移到C杆去。所以我可以先用B杆，帮我先”暂存”这上面的n-1个盘子。但是每次只能移动一个圆盘，所以我要借助剩下的杆子，也就是C杆，来协助把这n-1个盘子移到B杆上，然后才能把最大的盘子移到C杆上面去。当把最大的盘子移到C杆之后，剩下的问题就简单了，我只需要将剩下的n-1个盘子移到C杆就完成目标了(同样要借助剩下的杆子)。问题分析完毕，那么用简略的语言总结一下:

首先，以A杆作为起始杆，借助C杆作为中间杆(起协助作用)，将n-1个盘子移至B杆；
其次，将底下”最大的盘子”从A杆(起始杆)移至C杆(目标杆)；
最后，以B杆作为起始杆，借助A杆作为中间杆(起协助作用)，将n-1个盘子移至C杆；

而核心问题来了，每次只能移动一个圆盘，所以第一步移动n-1个盘子移至B杆的操作显然是不能一蹴而就的，除非当n-1等于1的时候，就可以直接移动了，因此第一步移动n-1个盘子移至B杆的操作还要继续分解，直至分解成可以直接操作的子问题。而该问题的分解过程与上述过程完全一致，因此依旧是递归这个过程分解原问题。同样的，最后一步的过程以此类推。这样，原问题就被分解成两个n-1阶的子问题和一个1阶的子问题。下面用简单的数学语言概括一下(设n阶汉诺塔问题为$f(n)$)，即为：

$$f(n) = \begin{cases} 1 &\mbox{if n = 1}\\ 2*f(n-1)+1 &\mbox{if n $\geq$ 1 } \end{cases}$$

下面简单证明为什么这样的做法是步数最小的做法:

数学归纳法证明过程如下:

当n == 1，结果显然为1。

假设$f(n-1)$确实是把n-1个盘子集体挪动的最小步数，我们要证明$f(n)$是把n个盘子集体挪动的最小步数。

1.在把n个盘子从A移动到C的过程中，必然存在一步，是把最大的盘子从A拿出来。要想把最大的盘子从A移动到别的某个柱子上（B或C），就必须保证剩下的n-1个盘子先移走，得好好堆在剩下那个柱子（C或B）上。要保证n-1个盘子都在剩下那个柱子上，至少得付出$f(n-1)$次移动。

2.在把n个盘子从A移动到C的过程中，必然存在一步，是最大的盘子被放到了C上，而且此后再也没动过。在这步实行之前，最大的盘子要么在A要么在B上，而相应地别的n-1个盘子要么在B要么在A上。在这步实施之后，我们只要花至少$f(n-1)$的步数把n-1个盘子从要么B要么A挪动到C上就行了。这些步数必然和步骤1中的步数不重叠，因为这时候最大盘子在C上，而步骤1中最大盘子在A上。

3.最大的盘子至少被挪动了一次。而且这一次肯定没被算在步骤1或步骤2的”至少$f(n-1)$步”中，因为后者只挪动较小的那n-1个盘子。

综上所述:$f(n)$的最小值即为:$f(n) = f(n-1) + 1 + f(n-1) = 2 * f(n-1) + 1$
得证

有了递推公式，那么是否可以得到通项公式呢？我们观察这个式子的前几项：
$f(1) = 1$

$f(2) = 2 * f(1) + 1 = 3$

$\begin {aligned} f(3) &= 2 * f(2) + 1 \\      &= 2 * (2 * f(1) + 1) + 1 \\      &= 2^2 * f(1) + 2^1 * 1 + 1(2^0) \\      &= 2^3 - 1 \\      &= 7 \end {aligned}$

$\begin {aligned} f(4) &= 2 * f(3) + 1 \\      &= 2 * (2 * f(2) + 1) + 1 \\      &= 2^2 * f(2) + 2^1 * 1 + 1(2^0) \\      &= 2^2 * (2 * f(1) + 1) + 2^1 * 1 + 2^0 \\      &= 2^4 - 1 \\      &= 15 \end {aligned}$

$...$
很显然，这是一个等比数列的求和问题，则：
$f(n) = 2^0 + 2^1 + 2^2 + ... + 2^{n-2} + 2^{n-1} = 2^n - 1$

即得通项公式为:

$$f(n) = 2^n - 1$$

实际上，所有原问题分解成子问题的过程，用图表示的话，是一棵三叉树，最后无法再分解的子问题即为该三叉树的叶节点，而整个原问题的规模即为所有子问题的和，即该三叉树叶节点节点总数。
示例代码:

package month12.day12;

import java.util.Scanner;

/**
 * Created by Administrator on 2016/12/12.
 */
public class TestForHanoi {
    public static void main(String args[]) {
        Scanner scanner = new Scanner(System.in);
        while (scanner.hasNextInt()) {
            int number = scanner.nextInt();
            hanoi('A','B','C', number);
            System.out.println("总的步数为:" + ((1 << number) - 1));     //加减法的运算符优先级更高
        }
    }

    static void hanoi(char startPos, char transPos, char targPos, int n) {
        if (n == 1) {
            move(startPos, targPos);
            return;
        } else {
            hanoi(startPos, targPos, transPos, n - 1);
            move(startPos, targPos);
            hanoi(transPos, startPos, targPos, n - 1);
        }
    }

    static void move(char startPos, char targPos) {
        System.out.println(startPos + " -> " + targPos);
    }
}

程序运行结果:

1
A -> C
总的步数为:1
2
A -> B
A -> C
B -> C
总的步数为:3
3
A -> C
A -> B
C -> B
A -> C
B -> A
B -> C
A -> C
总的步数为:7
4
A -> B
A -> C
B -> C
A -> B
C -> A
C -> B
A -> B
A -> C
B -> C
B -> A
C -> A
B -> C
A -> B
A -> C
B -> C
总的步数为:15

附录:四个盘子的移动过程: