这篇博客所有的数据和代码都在GitHub上可以找到,特别是编程题需要的.mat文件需要到Github上下载。下面我会把题目要求、代码和实验结果贴出来,如果有什么错误的地方,希望大家可以提出来。
1.下面的几道题可能会用到如下的程序:
(a)写一个程序产生服从d维正态分布
N(μ,Σ)
的随机样本。
(b)写一个程序计算一给定正态分布及先验概率
P(ωi)
的判别函数(
gi(x)=−12(x−μi)tΣ−1i(x−μi)−d2ln2π−12ln|Σi|+lnP(ωi)
)。
(c)写一个程序计算任意两点间的欧氏距离。
(d)在给定协方差矩阵
Σ
的情况条件下,写一个程序计算任意一点x到均值
μ
间的Mahalanobis距离。
CH2_1_a.m: Generate random vectors from the multivariate normal distribution.
function r = CH2_1_a(u, sigma, n)
% function r = CH2_1_a(u, sigma, n)
% Generate random vectors from the multivariate normal distribution.
% Inputs:
% u - Mean of distribution
% sigma - Covariance matrix of distribution
% n - Number of vectors
%
% Outputs:
% r - Matrix of random vectors
r = mvnrnd(u, sigma, n);
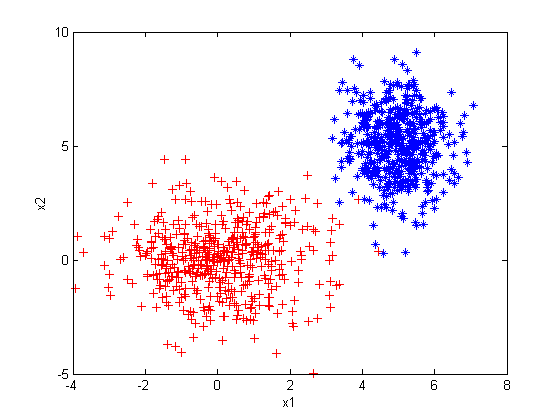
endCH2_1_a_test.m: Generate two normal distributions and plot.
% generate a normal distribution
u1 = [0, 0];
sigma1 = [2 0; 0 2];
r1 = CH2_1_a(u1, sigma1, 500);
plot(r1(:, 1), r1(:, 2), 'r+');
hold on;
% generate another normal distribution
u2 = [5, 5];
sigma2 = [.5 0; 0 2];
r2 = CH2_1_a(u2, sigma2, 500);
plot(r2(:, 1), r2(:, 2), '*');
xlabel('x1'), ylabel('x2');CH2_1_b.m: Discriminant function of a normal distribution given prior probability.
function g = CH2_1_b(x, u, sigma, P)
% function g = CH2_1_b(x, u, sigma, P)
% Discriminant function of a normal distribution given prior probability.
% Inputs:
% x - Input vector
% u - Mean of distribution
% sigma - Covariance matrix of distribution
% P - Prior probability
%
% Ouputs:
% g - Discriminant result
g = -0.5*(x - u)'*inv(sigma)*(x - u) - size(u, 1)/2.0*log(2*pi) - 0.5*log(det(sigma)) + log(P);
endCH2_1_c.m: Calculate the Euclidean distance between two vectors.
function E_dist = CH2_1_c(x1, x2)
% function E_dist = CH2_1_c(x1, x2)
% Calculate the Euclidean distance between two vectors.
% Inputs:
% x1 - Vector x1
% x2 - Vector x2
%
% Outputs:
% E_dist - Euclidean distance
E_dist = sqrt(sum((x1 - x2).^2));
endCH2_1_d.m: Calculate the Mahalanobis distance of a vector.
function M_dis = CH2_1_d(x, u, sigma)
% function M_dis = CH2_1_d(x, u, sigma)
% Calculate the Mahalanobis distance of a vector.
% Inputs:
% x - Input Vector
% u - Mean of distribution
% sigma - Covariance matrix of distribution
%
% Outputs:
% M_dis - Mahalanobis distance
M_dis = sqrt((x - u)'*inv(sigma)*(x - u));
end2.参考上机练习1(b),并考虑将上面表格中的10个样本点进行分类的问题,假设分布是正态的。
(a)假设前面两个类别的先验概率相等(
P(ω1)=P(ω2)=1/2
,且
P(ω3)=0)
,仅利用
x1
特征值为这两类判别设计一个分类器。
(b)确定样本的经验训练误差,即误分点的百分比。
(c)利用Bhattacharyya界来界定对该分布所产生的新模式进行分类会产生的误差。
(d)现在利用两个特征值
x1
和
x2
,重复以上各步。
(e)利用所有3个特征值重复以上各步。
(f)讨论所得的结论。特别是,对于一有限的数据集,是否有可能在更高的数据维数下经验误差会增加? 可能
CH2_2.m: Generate classification model of two classes, then calculate the classification error and the Bhattacharyya bound.
function [model, error, Bbound] = CH2_2(patterns, targets, c1, c2, P1, P2, dim)
% function [model, error, Bbound] = CH2_2(patterns, targets, c1, c2, P1, P2, dim)
% Generate classification model of two classes, then calculate the classification
% error and the Bhattacharyya bound.
% Inputs:
% patterns - Input matrix
% targets - Input matrix classes
% c1 - Class1
% c2 - Class2
% P1 - Prior probability of c1
% P2 - Prior probability of c2
% dim - Dimensions of input vector
%
% Outputs:
% model - Classification model
% error - Classification error
% Bbound - Bhattacharyya bound
%% Generate classification model
% matrices of two classes
x1 = patterns(1:dim, targets == c1);
x2 = patterns(1:dim, targets == c2);
% mean of two matrices
u1 = mean(x1, 2);
u2 = mean(x2, 2);
% covariance matrix of two matrices
sigma1 = cov(x1');
sigma2 = cov(x2');
% generate model
model.u1 = u1;
model.u2 = u2;
model.sigma1 = sigma1;
model.sigma2 = sigma2;
model.P1 = P1;
model.P2 = P2;
%% Calculate the classification error
col1 = size(x1, 2);
col2 = size(x2, 2);
result1 = zeros(col1, 1);
result2 = zeros(col2, 1);
% classification result
for i = 1:col1
if CH2_1_b(x1(:, i), model.u1, model.sigma1, model.P1) >= CH2_1_b(x1(:, i), model.u2, model.sigma2, model.P2)
result1(i) = c1;
else
result1(i) = c2;
end
end
for i = 1:col2
if CH2_1_b(x2(:, i), model.u2, model.sigma2, model.P2) >= CH2_1_b(x2(:, i), model.u1, model.sigma1, model.P1)
result2(i) = c2;
else
result2(i) = c1;
end
end
% classification error
error_num = size(find(result1 == c2), 1) + size(find(result2 == c1), 1);
error = error_num/(col1 + col2);
%% Bhattacharyya bound
Bbound = Bhattacharyya(u1, sigma1, u2, sigma2, P1);
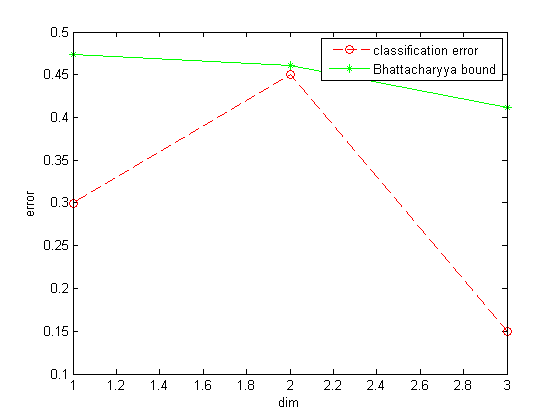
CH2_2_test.m: Plot classification error and Bhattacharyya bound.
load CH2.mat
error_vec = zeros(3, 1);
Bbound_vec = zeros(3, 1);
% calculate classification error and Bhattacharyya bound
for i = 1:3
[model, error, Bbound] = CH2_2(patterns, targets, 1, 2, 0.5, 0.5, i);
model_cell{i} = model;
error_vec(i) = error;
Bbound_vec(i) = Bbound;
end
% plot
plot(1:3, error_vec, '--ro', 1:3, Bbound_vec, '-g*');
xlabel('dim');
ylabel('error');
legend('classification error', 'Bhattacharyya bound');3.对于类别 ω1 和 ω3 重复上机题2。
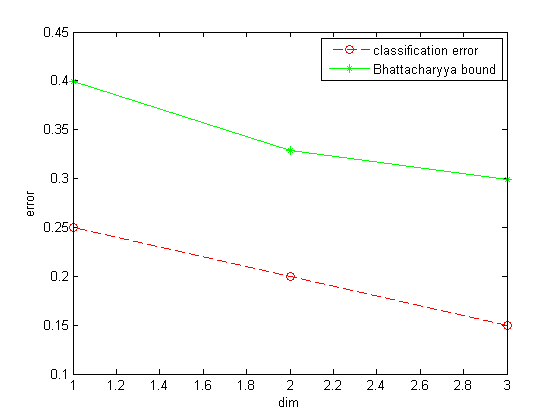
CH2_3.m: Plot classification error and Bhattacharyya bound.
load CH2.mat
error_vec = zeros(3, 1);
Bbound_vec = zeros(3, 1);
% calculate classification error and Bhattacharyya bound
% same to CH2_2_test
% modify two classes and two prior probabilities
for i = 1:3
[model, error, Bbound] = CH2_2(patterns, targets, 1, 3, 0.5, 0.5, i);
model_cell{i} = model;
error_vec(i) = error;
Bbound_vec(i) = Bbound;
end
% plot
plot(1:3, error_vec, '--ro', 1:3, Bbound_vec, '-g*');
xlabel('dim');
ylabel('error');
legend('classification error', 'Bhattacharyya bound');4.考虑上机题2中的3个类别,设
P(ωi)=1/3
。
(a)以下各测试点与上机练习2中各类别均值间的Mahalanobis距离分别是多少:
(1,2,1)t,(5,3,2)t,(0,0,0)t,(1,0,0)t
。
(b)对以上各点进行分类。
(c)若设
P(ω1)=0.8,P(ω2)=P(ω3)=0.1
,再对以上测试点进行分类。
CH2_4.m: Calculate the Mahalanobis distance with three classes, then classify the vectors.
function [M_dist, class] = CH2_4(x, patterns, targets, P)
% function [M_dist, class] = CH2_4(x, patterns, targets, P1, P2, P3)
% Calculate the Mahalanobis distance with three classes, then classify the
% vectors.
% Inputs:
% x - Input vector
% patterns - Input matrix
% targets - Input matrix classes
% P - Prior probability of class 1,2,3
%
% Outputs:
% M_dist - Mahalanobis distance
% class - classification result
%% Mahalanobis distance
m = size(patterns, 1);
for i = 1:m
p = patterns(:, targets == i);
u{i} = mean(p, 2);
sigma{i} = cov(p');
end
for i = 1:m
M_dist(i) = CH2_1_d(x, u{i}, sigma{i});
end
%% classification
class = 0; max_g = -Inf;
for i = 1:m
g = CH2_1_b(x, u{i}, sigma{i}, P(i));
if g > max_g
class = i;
max_g = g;
end
end
endCH2_4_test.m: Test CH2_4.m with four vectors.
load CH2.mat
v = [1 2 1; 5 3 2; 0 0 0; 1 0 0]';
%% P = [1/3 1/3 1/3]
P = [1/3 1/3 1/3];
fprintf('The prior probability of three classes is : [1/3 1/3 1/3]\n');
for i = 1:size(v, 2)
x = v(:, i);
[M_dist, class] = CH2_4(x, patterns, targets, P);
fprintf('The Mahalanobis distance between vector %d and three classes is %f, %f, %f\n', ...
i, M_dist(1), M_dist(2), M_dist(3));
fprintf('Vector %d belongs to class %d\n\n', i, class);
end
fprintf('\n\n\n');
%% P = [0.8 0.1 0.1]
P = [0.8 0.1 0.1];
fprintf('The prior probability of three classes is : [0.8 0.1 0.1]\n');
for i = 1:size(v, 2)
x = v(:, i);
[M_dist, class] = CH2_4(x, patterns, targets, P);
fprintf('The Mahalanobis distance between vector %d and three classes is %f, %f, %f\n', ...
i, M_dist(1), M_dist(2), M_dist(3));
fprintf('Vector %d belongs to class %d\n\n', i, class);
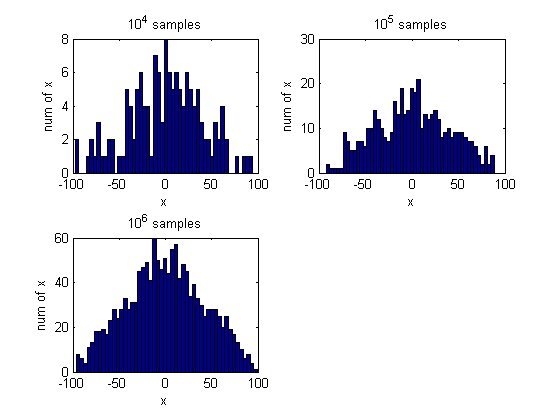
end5.通过以下步骤说明这样一个事实:大量独立的随机变量的平均将近似为一高斯分布。
(a)写一个程序,从一均匀分布U(
xl,xu
)中产生n个随机整数。(有些计算机系统在其函数库中包含了这样的函数调用。)
(b)现在写一个程序,从范围
−100≤xl<xu≤+100
中随机取
xl
和
xu
,以及在范围
0<n≤1000
中随机取n的值(样本数)。
(c)通过以上所述的方式累计产生
104
个样本点,并绘制一直方图。
(d)计算该直方图的均值和标准差,并绘图。
(e)对于
105
和
106
个样本点分别重复以上步骤,讨论所得结论。
CH2_5.m: The script is to prove that the average of a large number of independent random variables follows Gauss distribution.
% The script is to prove that the average of a large number of
% independent random variables follows Gauss distribution.
% 10^4, 10^5, 10^6 samples
% 1. randomly pick xl and xu, -100 <= xl < xu <= 100
% 2. randomly pick n, 0 <= n <= 1000
% 3. randomly pick n numbers from [xl xu]
% 4. calculate the average of the n numbers
for i = 4:6
h = zeros(1, 0);
y = zeros(1, 0);
while size(h, 2) < 10^i
x = randi([-100 100], 1, 2);
if min(x) == max(x)
continue;
end
xl = min(x);
xu = max(x);
n = randi([0 1000], 1, 1);
v = randi([xl xu], 1, n);
y = [y mean(v)];
h = [h y];
end
% hist
subplot(2, 2, i - 3);
hist(y, 50);
xlabel('x'), ylabel('num of x');
title(['10^',num2str(i),' samples']);
fprintf('10^%d samples:\n', i);
fprintf('mean:%f std:%f\n\n', mean(y), std(y));
end6.根据以下步骤测试经验误差是如何接近或不接近Bhattacharyya界的:
(a)写一个程序产生d维空间的样本点,服从均值为
μ
和协方差矩阵
Σ
的正态分布。
(b)考虑正态分布
p(x|ω1)∼N((10),I)
和
p(x|ω2)∼N((−10),I)
且
P(ω1)=P(ω2)=0.5
。说明贝叶斯判决边界。
(c)产生n = 100个点(50个
ω1
类点点,50个
ω2
类的点),并计算经验误差。
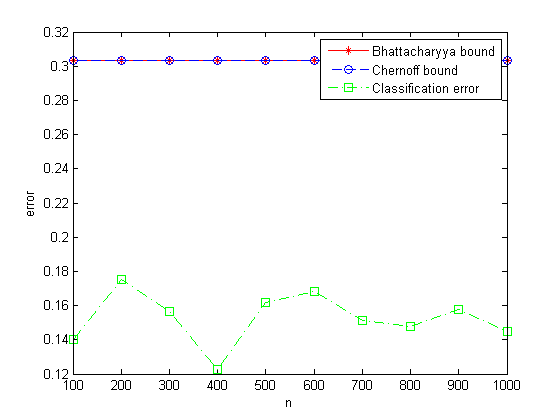
(d)对于不断增加的n值重复以上步骤,
100≤n≤1000
,步长量为100,并绘出所得的经验误差。
(e)讨论所得的结论。特别是,经验误差是否可能比Bhattacharyya或Chernoff界还大。 可能
CH2_6.m: Calculate the classification error of two classes.
function [error, Bbound, Cbound] = CH2_6(u1, sigma1, u2, sigma2, P1, P2)
% function error = CH2_6(u1, sigma1, u2, sigma2, P1, P2)
% Calculate the classification error of two classes.
% Inputs:
% u1 - Mean of class1
% sigma1 - Covariance matrix of class1
% u2 - Mean of class2
% sigma2 - Covariance matrix of class2
% P1 - Prior probability of class1
% P2 - Prior probability of class2
%
% Outputs:
% error - Classification error
% Bbound - Bhattacharyya bound
% Cbound - Chernoff bound
%% plot Gauss distribution
% Gauss distribution
[x1_1, x1_2] = meshgrid(linspace(-4, 6, 100)', linspace(-5, 5, 100)');
x1 = [x1_1(:) x1_2(:)];
p1 = P1*mvnpdf(x1, u1', sigma1);
surf(x1_1, x1_2, reshape(p1, 100, 100));
hold on;
[x2_1, x2_2] = meshgrid(linspace(-6,4,100)', linspace(-5,5,100)');
x2 = [x2_1(:) x2_2(:)];
p2 = P2*mvnpdf(x2, u2', sigma2);
surf(x2_1, x2_2, reshape(p2, 100, 100));
xlabel('x1'), ylabel('x2'), zlabel('p');
% Obviously, surf x1 = 0 is the Bayes decision boundary.
%% classification error, Bhattacharyya bound, Chernoff bound
figure;
Bbound = Bhattacharyya(u1, sigma1, u2, sigma2, P1);
Cbound = Chernoff(u1, sigma1, u2, sigma2, P1);
for n = 100:100:1000
r1 = CH2_1_a(u1, sigma1, n/2);
r2 = CH2_1_a(u2, sigma2, n/2);
% error1_2: number of class1 misclassified to class2
% error2_1: number of class2 misclassified to class1
error1_2 = 0;
error2_1 = 0;
for i = 1:size(r1, 1)
% class1 misclassified to class2
if(CH2_1_b(r1(i, :)', u1, sigma1, P1) < CH2_1_b(r1(i, :)', u2, sigma2, P2))
error1_2 = error1_2 + 1;
end
% class2 misclassified to class1
if(CH2_1_b(r2(i, :)', u2, sigma2, P2) < CH2_1_b(r2(i, :)', u1, sigma1, P1))
error2_1 = error2_1 + 1;
end
end
error(n/100) = (error1_2 + error2_1)/n;
end
plot(100:100:1000, Bbound*ones(1, 10), '-r*', ...
100:100:1000, Cbound*ones(1, 10), '--bo', ...
100:100:1000, error, '-.gs');
xlabel('n'), ylabel('error');
legend('Bhattacharyya bound', 'Chernoff bound', 'Classification error');
endCH2_6_test.m: Test CH2_6.m.
u1 = [1 0]';
sigma1 = [1 0; 0 1];
u2 = [-1 0]';
sigma2 = [1 0; 0 1];
[error, Bbound, Cbound] = CH2_6(u1, sigma1, u2, sigma2, 0.5, 0.5);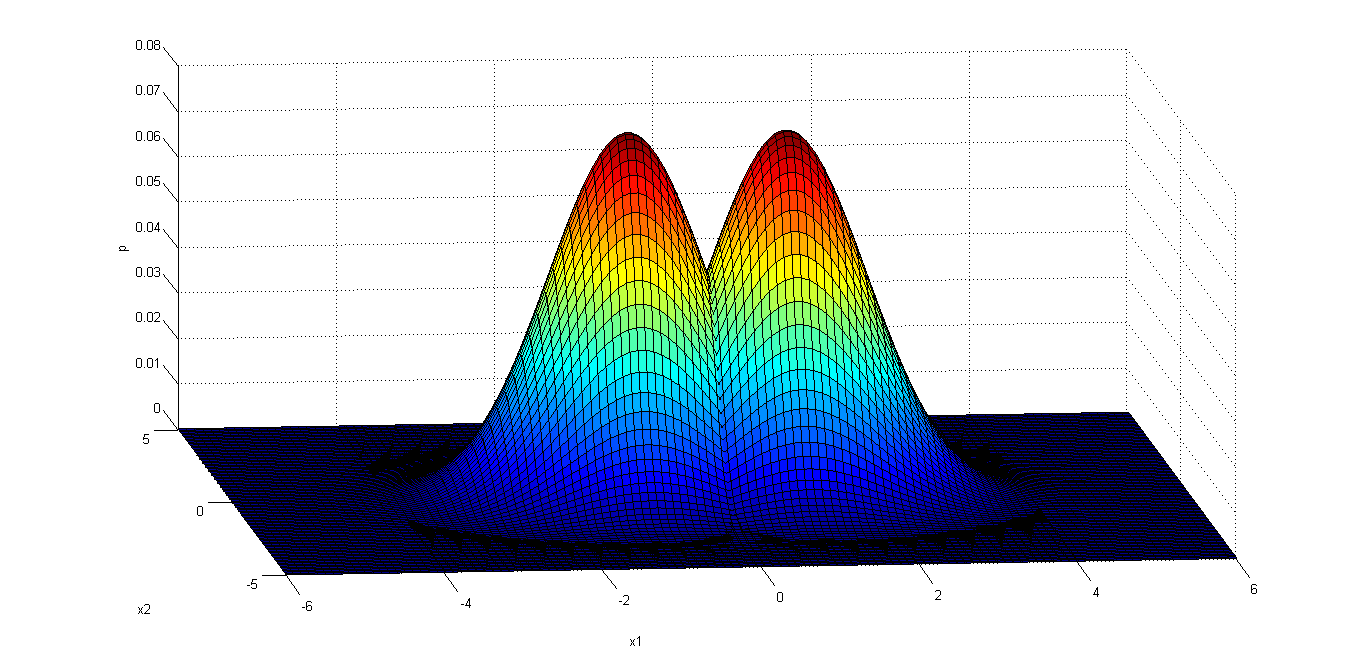
7.考虑两个一维正态分布
p(x|ω1)∼N(−0.5,1)
及
p(x|ω2)∼N(+0.5,1)
,且
P(ω1)=P(ω2)=0.5
。
(a)计算一个贝叶斯分类器的Bhattacharyya误差界。
(b)用一个误差函数
erf(⋅)
的形式表示实际误差率。
(1−erf(2√/4))/2
(c)通过数值积分(或其他方式)估计此实际误差,精确到4位有效数字。
(d)分别产生每类10个样本点,并确定用以上贝叶斯分类器进行分类时的经验误差。(必须对每一套数据重新计算判决边界)
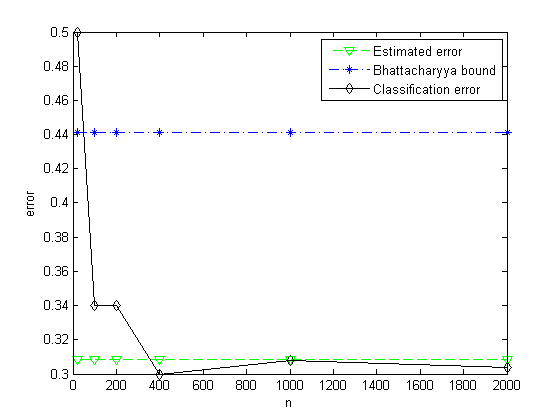
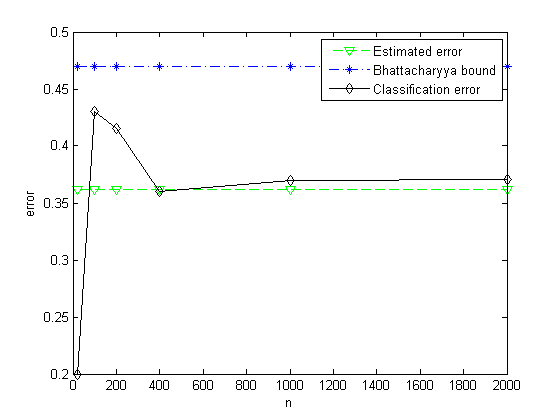
(e)通过重复前面的步骤,并分别从两种分布中各取50、100、200、500及1000个样本点,绘制出经验误差作为取自两种分布的样本点数的函数图。比较渐近于实际误差的经验误差同Bhattacharyya误差界。
CH2_7.m: Calculate the Bhattacharyya bound, estimated error and a series of classification error of two Gauss distribution.
function [Eerror, Bbound, Cerror] = CH2_7(u1, sigma1, u2, sigma2, P1, P2)
% function [Eerror, Bbound, Cerror] = CH2_7(u1, sigma1, u2, sigma2, P1, P2)
% Calculate the Bhattacharyya bound, estimated error and a
% series of classification error of two Gauss distribution.
% Inputs:
% u1 - Mean of class1
% sigma1 - Covariance matrix of class1
% u2 - Mean of class2
% sigma2 - Covariance matrix of class2
% P1 - Prior probability of class1
% P2 - Prior probability of class2
%
% Outputs:
% Eerror - Estimated error
% Bbound - Bhattacharyya bound
% Cerror - Classification error
%% calculate the curve intersection point
eq1 = ['y = ' num2str(P1) '*1/sqrt(2*pi*' num2str(sigma1) ')*exp(-(x - ' num2str(u1) ')^2/(2*' num2str(sigma1) '))'];
eq2 = ['y = ' num2str(P2) '*1/sqrt(2*pi*' num2str(sigma2) ')*exp(-(x - ' num2str(u2) ')^2/(2*' num2str(sigma2) '))'];
[inter_x, inter_y] = solve(eq1, eq2);
inter_x = double(inter_x);
inter_y = double(inter_y);
%% plot Gauss distribution
% Gauss distribution
x = (-5:0.1:5)';
y1 = P1*1/sqrt(2*pi*sigma1)*exp(-(x - u1).^2/(2*sigma1));
y2 = P2*1/sqrt(2*pi*sigma2)*exp(-(x - u2).^2/(2*sigma2));
plot(x, [y1 y2]);
hold on;
plot(inter_x, inter_y, 'rx', 'LineWidth', 2, 'MarkerSize', 10);
for i = 1:size(inter_x, 1)
text(inter_x(i) + 0.2, inter_y(i), ['\leftarrow (' num2str(inter_x(i)) ', ' ...
num2str(inter_y(i)) ')']);
end
xlabel('x'), ylabel('y');
legend(['N(' num2str(u1) ', ' num2str(sigma1) ')'], ['N(' num2str(u2) ', ' num2str(sigma2) ')'], 'intersection point');
%% Bhattacharyya bound
Bbound = Bhattacharyya(u1, sigma1, u2, sigma2, P1);
%% estimated error using numerical integration
% the intersection area of two Gauss distribution means error
syms x;
if size(inter_x, 1) == 1
Eerror = double(int(P1*1/sqrt(2*pi*sigma1)*exp(-(x - u1)^2/(2*sigma1)), inter_x, Inf)) + ...
double(int(P2*1/sqrt(2*pi*sigma2)*exp(-(x - u2)^2/(2*sigma2)), -Inf, inter_x));
else if size(inter_x, 1) == 2
Eerror = double(int(P1*1/sqrt(2*pi*sigma1)*exp(-(x - u1)^2/(2*sigma1)), inter_x(1), inter_x(2))) + ...
double(int(P2*1/sqrt(2*pi*sigma2)*exp(-(x - u2)^2/(2*sigma2)), -Inf, inter_x(1))) + ...
double(int(P2*1/sqrt(2*pi*sigma2)*exp(-(x - u2)^2/(2*sigma2)), inter_x(2), Inf));
end
end
%% classification error
m = 1;
vec = [10 50 100 200 500 1000];
for n = vec
r1 = CH2_1_a(u1, sigma1, round(P1*2*n));
r2 = CH2_1_a(u2, sigma2, 2*n - round(P1*2*n));
% error1_2: number of class1 misclassified to class2
% error2_1: number of class2 misclassified to class1
error1_2 = 0;
error2_1 = 0;
for i = 1:size(r1, 1)
% class1 misclassified to class2
if(CH2_1_b(r1(i, :)', u1, sigma1, P1) < CH2_1_b(r1(i, :)', u2, sigma2, P2))
error1_2 = error1_2 + 1;
end
end
for j = 1:size(r2, 1)
% class2 misclassified to class1
if(CH2_1_b(r2(j, :)', u2, sigma2, P2) < CH2_1_b(r2(j, :)', u1, sigma1, P1))
error2_1 = error2_1 + 1;
end
end
Cerror(m) = (error1_2 + error2_1)/(2*n);
m = m + 1;
end
figure;
plot(2*vec, Eerror*ones(1, size(vec, 2)), '--gv', ...
2*vec, Bbound*ones(1, size(vec, 2)), '-.b*', 2*vec, Cerror, '-kd');
xlabel('n'), ylabel('error');
legend('Estimated error', 'Bhattacharyya bound', 'Classification error');
endCH2_7_test.m: Test CH2_7.m.
u1 = -0.5;
sigma1 = 1;
u2 = 0.5;
sigma2 = 1;
P1 = 0.5;
P2 = 0.5;
[Eerror, Bbound, Cerror] = CH2_7(u1, sigma1, u2, sigma2, P1, P2);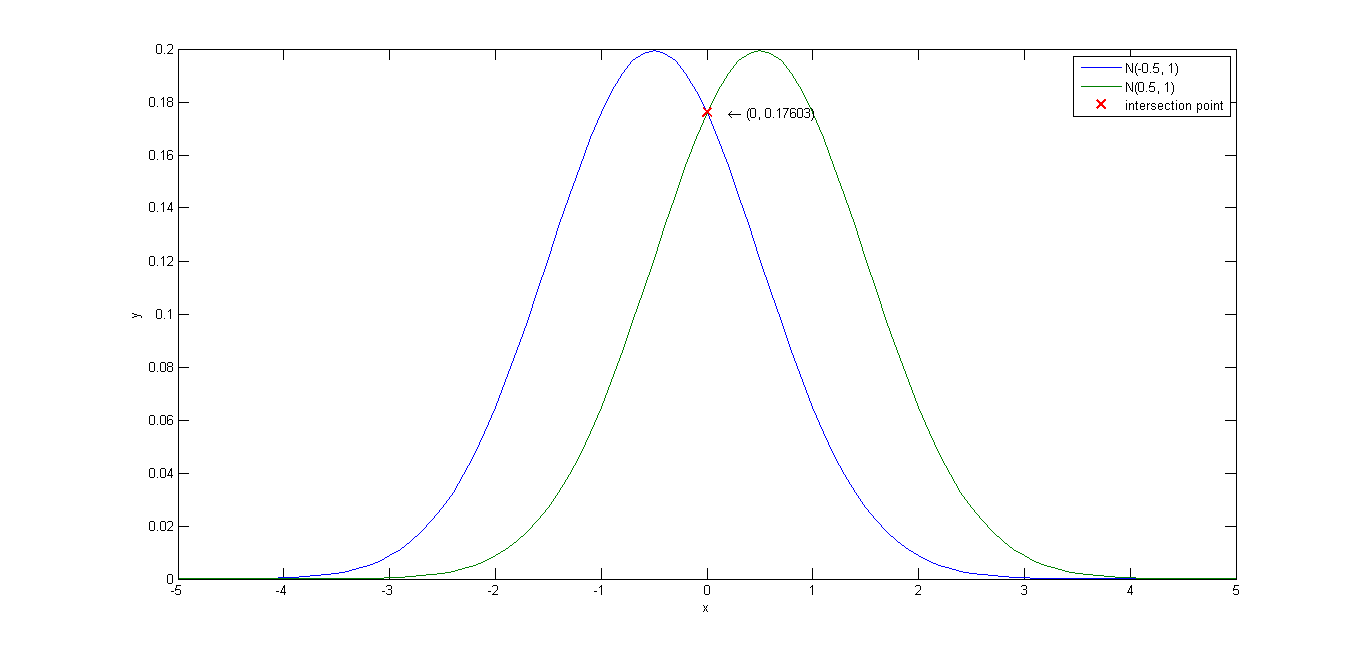
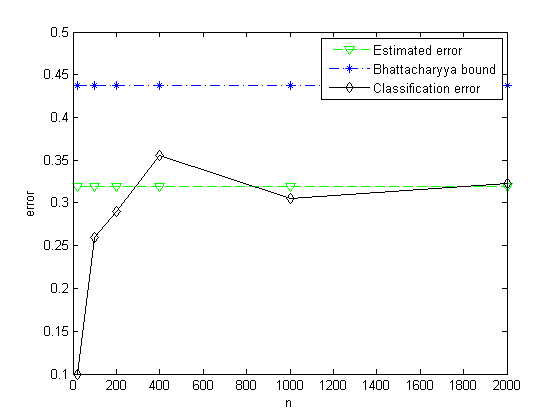
8.在以下条件下重复上机题7:
(a)
p(x|ω1)∼N(−0.5,2)
及
p(x|ω2)∼N(+0.5,2)
,
P(ω1)=2/3
及
P(ω2)=1/3
。
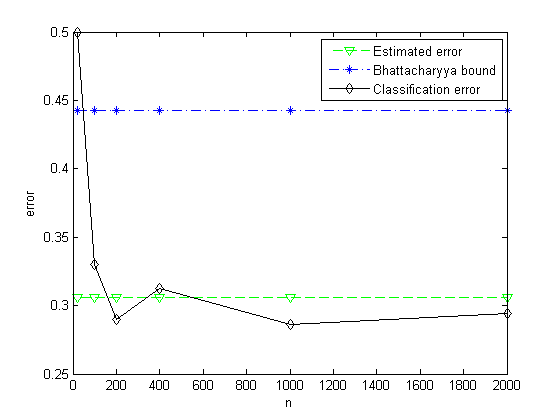
(b)
p(x|ω1)∼N(−0.5,2)
及
p(x|ω2)∼N(+0.5,2)
,
P(ω1)=1/2
及
P(ω2)=1/2
。
(c)
p(x|ω1)∼N(−0.5,3)
及
p(x|ω2)∼N(+0.5,1)
,
P(ω1)=1/2
及
P(ω2)=1/2
。
CH2_8_a.m: Test CH2_7.m with two Gauss distribution.
u1 = -0.5;
sigma1 = 2;
u2 = 0.5;
sigma2 = 2;
P1 = 2/3;
P2 = 1/3;
[Eerror, Bbound, Cerror] = CH2_7(u1, sigma1, u2, sigma2, P1, P2);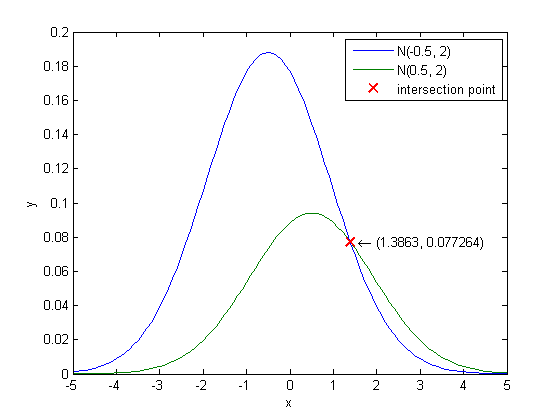
CH2_8_b.m: Test CH2_7.m with two Gauss distribution.
u1 = -0.5;
sigma1 = 2;
u2 = 0.5;
sigma2 = 2;
P1 = 1/2;
P2 = 1/2;
[Eerror, Bbound, Cerror] = CH2_7(u1, sigma1, u2, sigma2, P1, P2);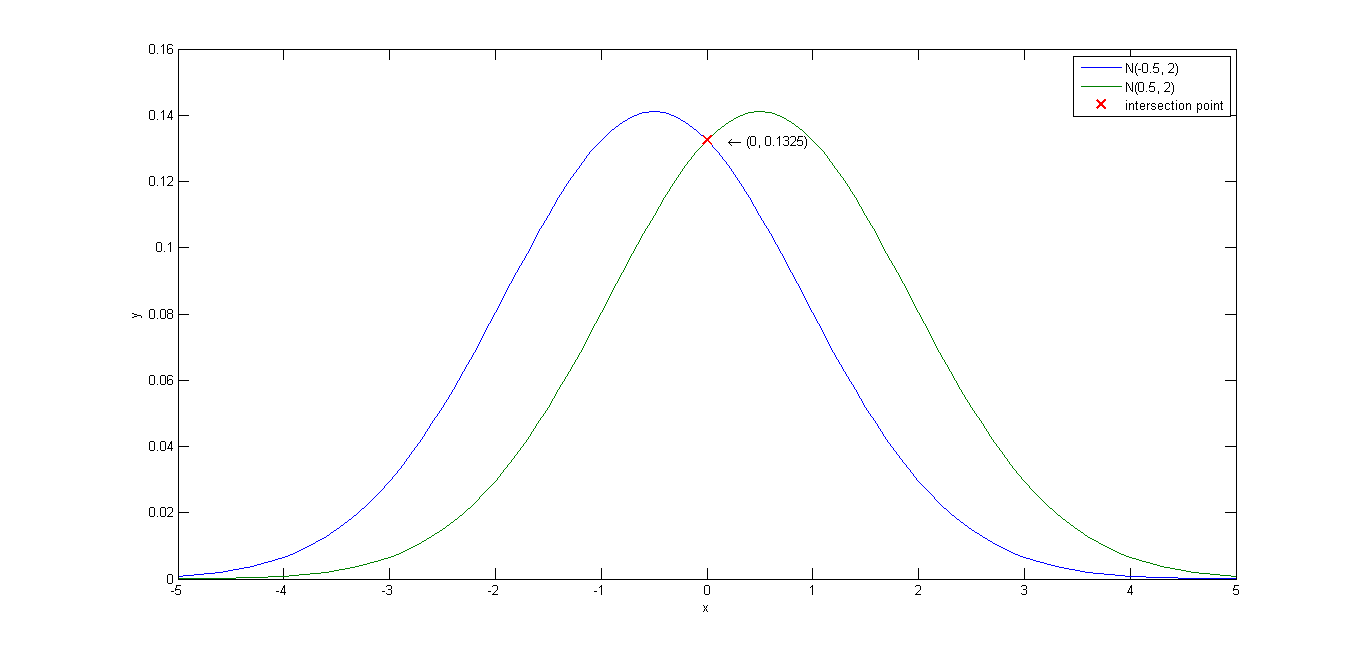
CH2_8_c.m: Test CH2_7.m with two Gauss distribution.
u1 = -0.5;
sigma1 = 3;
u2 = 0.5;
sigma2 = 1;
P1 = 1/2;
P2 = 1/2;
[Eerror, Bbound, Cerror] = CH2_7(u1, sigma1, u2, sigma2, P1, P2);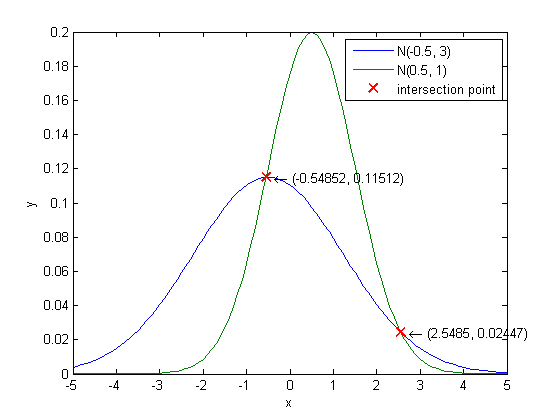
Bhattacharyya.m: Find the Bhattacharyya bound given means and covariances of single gaussian distributions.
function Perror = Bhattacharyya(u1, sigma1, u2, sigma2, P1)
% function Perror = Bhattacharyya(mu1, sigma1, mu2, sigma2, p1)
% Find the Bhattacharyya bound given means and covariances of single
% gaussian distributions.
% Inputs:
% u1 - Mean of class1
% sigma1 - Covariance matrix of class1
% u2 - Mean of class2
% sigma2 - Covariance matrix of class2
% P1 - Probability of class1
%
% Outputs
% Perror - Error bound
k_half = 1/8*(u2 - u1)'*inv((sigma1 + sigma2)/2)*(u2 - u1) + 1/2*log(det((sigma1+sigma2)/2)/sqrt(det(sigma1)*det(sigma2)));
Perror = sqrt(P1*(1 - P1))*exp(-k_half);Chernoff.m: Find the Chernoff bound given means and covariances of single gaussian distributions.
function Perror = Chernoff(u1, sigma1, u2, sigma2, P1)
% function Perror = Chernoff(u1, sigma1, u2, sigma2, P1)
% Find the Chernoff bound given means and covariances of single gaussian distributions.
% Inputs:
% u1 - Mean of class1
% sigma1 - Covariance matrix of class1
% u2 - Mean of class2
% sigma2 - Covariance matrix for class2
% P1 - Prior probability of class1
%
% Outputs
% Perror - Error bound
beta = linspace(0, 1, 100);
k = zeros(1, length(beta));
% calculate k(beta)
for i = 1:length(beta),
k(i) = beta(i)*(1 - beta(i))/2*(u2 - u1)'*inv(beta(i)*sigma1 + (1 - beta(i))*sigma2)*(u2 - u1) + ...
1/2*log(det(beta(i)*sigma1 + (1 - beta(i))*sigma2)/(det(sigma1)^beta(i)*det(sigma2)^(1 - beta(i))));
end
% find the minimum of exp(-k)
[m, index] = min(exp(-k));
min_beta = beta(index);
Perror = P1^min_beta*(1 - P1)^(1 - min_beta)*exp(-k(index));
% fprintf('min beta:%f\n', min_beta);
% plot(beta, exp(-k));




















 4868
4868











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








