广义线性模型

最新推荐文章于 2024-02-26 01:19:58 发布
最新推荐文章于 2024-02-26 01:19:58 发布
阅读量3.2k 收藏 9
点赞数 1
文章标签： R 统计学 数据科学实战 线性回归
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/lswbjtu/article/details/70767606
版权

广义线性模型

LSWBJTU
2017/4/24

前言

之前介绍了线性回归和方差分析，探索了线性模型能用于预测符合正态分布的响应变量（来自连续型和分类型预测变量）。尽管如此，仍然有很多情况，我们无法合理地假设独立变量符合正态分布，例如：

  • 输出变量是分类型。二元变量（0/1，yes／no，成功／失败），类别变量，都不属于正态分布。

  • 输出变量是个计数（统计交通事故次数），这些变量有值域上的限制，且非负。另外它们的均值和方差是相关联的，而正态分布的均值和方差是独立的，说明它们不是正态分布。

为此，我们在一般线性的基础上进行深入学习，来研究包含了非正态因变量的广义线性模型。

1.广义线性模型

这一节我们主要介绍两种重要的广义线性模型：Logistic regression（分类变量）和Possion regression（计数变量）。广义线性模型是线性模型的推广，它可以写成如下形式:

g(μr)=β0+∑pj=1βjXj 这里 g(μr) 是一个条件均值的函数，例如”logit”,”inverse”,”1/mu^2”这些在R包中称为link function.我们理解广义线性模型是通过g函数作用后变为线性模型，因而找到合适的link function g(x) 至关重要，下面是常用的link function：

这里写图片描述

  • glm()function的常用函数
summary()
coefficients();coef()
confint()
residuals()
anova()
plot()
predict()

2.Logistic regression

Logistic regression 用于从连续型和分类型预测变量中预测二元输出量，为此我们选取数据集Affairs，它记录了601组婚外情数据，变量包括性别，年龄，婚龄，是否有小孩，宗教信仰程度（1～5），学历、职业和婚姻的自我评价（1～5）。来看一些这个数据集的描述

library(AER)
data("Affairs")
attach(Affairs)
summary(Affairs)
##     affairs          gender         age         yearsmarried    children 
##  Min.   : 0.000   female:315   Min.   :17.50   Min.   : 0.125   no :171  
##  1st Qu.: 0.000   male  :286   1st Qu.:27.00   1st Qu.: 4.000   yes:430  
##  Median : 0.000                Median :32.00   Median : 7.000            
##  Mean   : 1.456                Mean   :32.49   Mean   : 8.178            
##  3rd Qu.: 0.000                3rd Qu.:37.00   3rd Qu.:15.000            
##  Max.   :12.000                Max.   :57.00   Max.   :15.000            
##  religiousness     education       occupation        rating     
##  Min.   :1.000   Min.   : 9.00   Min.   :1.000   Min.   :1.000  
##  1st Qu.:2.000   1st Qu.:14.00   1st Qu.:3.000   1st Qu.:3.000  
##  Median :3.000   Median :16.00   Median :5.000   Median :4.000  
##  Mean   :3.116   Mean   :16.17   Mean   :4.195   Mean   :3.932  
##  3rd Qu.:4.000   3rd Qu.:18.00   3rd Qu.:6.000   3rd Qu.:5.000  
##  Max.   :5.000   Max.   :20.00   Max.   :7.000   Max.   :5.000
table(affairs)
## affairs
##   0   1   2   3   7  12 
## 451  34  17  19  42  38
1).数据准备

简单来看，该数据包括女性315人，男性286人，年龄从17～57岁，其中430人有孩子。从table()函数结果来看，无婚外情包括451人。尽管婚外情次数不等，我们在这里主要关心婚外情是否存在（binary outcome），故将affairs变量转换成因子变量：

Affairs$ynaffair[affairs>0]<-1
Affairs$ynaffair[affairs==0]<-0
Affairs$ynaffair<-factor(Affairs$ynaffair,levels = c(0,1),labels = c("No","Yes"))
table(Affairs$ynaffair)
## 
##  No Yes 
## 451 150
2)运用logistic regression 模型:
fit<-glm(ynaffair~gender+age+yearsmarried+children+religiousness+education+occupation+rating,family = binomial(),data = Affairs)
summary(fit)
## 
## Call:
## glm(formula = ynaffair ~ gender + age + yearsmarried + children + 
##     religiousness + education + occupation + rating, family = binomial(), 
##     data = Affairs)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.5713  -0.7499  -0.5690  -0.2539   2.5191  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)    1.37726    0.88776   1.551 0.120807    
## gendermale     0.28029    0.23909   1.172 0.241083    
## age           -0.04426    0.01825  -2.425 0.015301 *  
## yearsmarried   0.09477    0.03221   2.942 0.003262 ** 
## childrenyes    0.39767    0.29151   1.364 0.172508    
## religiousness -0.32472    0.08975  -3.618 0.000297 ***
## education      0.02105    0.05051   0.417 0.676851    
## occupation     0.03092    0.07178   0.431 0.666630    
## rating        -0.46845    0.09091  -5.153 2.56e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 675.38  on 600  degrees of freedom
## Residual deviance: 609.51  on 592  degrees of freedom
## AIC: 627.51
## 
## Number of Fisher Scoring iterations: 4

从回归因子对应的p值看出，性别，育儿，教育，职业并不显著，因此，去除这几个变量后重新拟合。

fit.remove<-glm(ynaffair~age+yearsmarried+religiousness+rating,data=Affairs,family = binomial())
summary(fit.remove)
## 
## Call:
## glm(formula = ynaffair ~ age + yearsmarried + religiousness + 
##     rating, family = binomial(), data = Affairs)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.6278  -0.7550  -0.5701  -0.2624   2.3998  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)    1.93083    0.61032   3.164 0.001558 ** 
## age           -0.03527    0.01736  -2.032 0.042127 *  
## yearsmarried   0.10062    0.02921   3.445 0.000571 ***
## religiousness -0.32902    0.08945  -3.678 0.000235 ***
## rating        -0.46136    0.08884  -5.193 2.06e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 675.38  on 600  degrees of freedom
## Residual deviance: 615.36  on 596  degrees of freedom
## AIC: 625.36
## 
## Number of Fisher Scoring iterations: 4
3)剔除变量，调整模型

调整后的模型，每个变量均显著，我们用anova()函数来对比这两个模型的优劣。

anova(fit,fit.remove,test="Chisq")
## Analysis of Deviance Table
## 
## Model 1: ynaffair ~ gender + age + yearsmarried + children + religiousness + 
##     education + occupation + rating
## Model 2: ynaffair ~ age + yearsmarried + religiousness + rating
##   Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1       592     609.51                     
## 2       596     615.36 -4  -5.8474   0.2108

p值的结果表明，剔除变量的模型和全变量的模型预测的效果类似，即剔除的变量对模型的预测没有影响，故我们偏向于采用更加简单的模型。

4)解释模型的参数
coef(fit.remove)
##   (Intercept)           age  yearsmarried religiousness        rating 
##    1.93083017   -0.03527112    0.10062274   -0.32902386   -0.46136144

给予logistic回归的模型参数，变量都进行了对数化log(odd)，可用指数化还原变量的值：

exp(coef(fit.remove))
##   (Intercept)           age  yearsmarried religiousness        rating 
##     6.8952321     0.9653437     1.1058594     0.7196258     0.6304248
5)评估预测变量对输出结果概率的影响

利用predict()函数进行变量对模型预测结果的影响。首先创建一组随机的数据集，其中的age，yearsmarried，religiousness设为原数据集的均值，rating设置为1~5。

testdata<-data.frame(rating=c(1,2,3,4,5),age=mean(Affairs$age),yearsmarried=mean(Affairs$yearsmarried),religiousness=mean(Affairs$religiousness))
testdata$prob<-predict(fit.remove,newdata = testdata,type="response")
testdata
##   rating      age yearsmarried religiousness      prob
## 1      1 32.48752     8.177696      3.116473 0.5302296
## 2      2 32.48752     8.177696      3.116473 0.4157377
## 3      3 32.48752     8.177696      3.116473 0.3096712
## 4      4 32.48752     8.177696      3.116473 0.2204547
## 5      5 32.48752     8.177696      3.116473 0.1513079

固定其他四个变量之后，我们发现rating的值从1～5变化，导致婚外情概率从0.53降到0.15。 同样的，我们研究年龄的变化对结果的影响：

testdata<-data.frame(rating=mean(Affairs$rating),age=seq(17,57,10),yearsmarried=mean(Affairs$yearsmarried),religiousness=mean(Affairs$religiousness))
testdata$prob<-predict(fit.remove,newdata = testdata,type="response")
testdata
##    rating age yearsmarried religiousness      prob
## 1 3.93178  17     8.177696      3.116473 0.3350834
## 2 3.93178  27     8.177696      3.116473 0.2615373
## 3 3.93178  37     8.177696      3.116473 0.1992953
## 4 3.93178  47     8.177696      3.116473 0.1488796
## 5 3.93178  57     8.177696      3.116473 0.1094738

我们发现，年龄从17～57变化，婚外情概率从0.335降到0.11。可见rating的影响最大，其他的变量也可如此推断。

6)超散布性(overdispersion)

在数据分析和建模的过程中，我们通常需要假设数据变量服从某个分布，再利用数据和估计方法对参数进行估计，当分布被确定后，均值和方差也被确定，若此时观测数据的方差系统地大于分布假设条件下的方差，就出现了“超散布性”，若小于系统方差，则出现了“超聚集性”。

  • 一种用于检测超散布性的方法是比较残差偏离值(Residual deviance)和自由度的比率，如果 ϕ=Residualdeviance/Residualdf 大于1，则说明数据超散步性。 下面利用Affair数据及进行演示：
fit.remove$deviance/fit.remove$df.residual
## [1] 1.03248

值很接近1，说明“超散布性”不存在。

  • 另一种方法是，拟合模型两次，第一次family=binomial,第二次family=quasibinomial。然后进行卡方检验，原假设为 ϕ=1 。
fit.od<-glm(ynaffair~age+yearsmarried+religiousness+rating,family = binomial(),data=Affairs)
fit.new<-glm(ynaffair~age+yearsmarried+religiousness+rating,family = quasibinomial(),data=Affairs)
pchisq(summary(fit.new)$dispersion*fit.od$df.residual,fit.od$df.residual,lower=F)
## [1] 0.340122

P值结果为0.34，表明无显著性，证明“超散布性”不存在。

7)logistic 回归的扩展模型
  • 稳健logistic回归：glmRob()函数用于拟合稳健的广义线性模型，适用于拟合模型中数据存在离群点和强影响点。
  • 多项式分布回归：响应变量包含两个以上的无序类（例如已婚，寡居，离婚）时，可使用mlogit()函数拟合多项logistic回归。
  • 序数logistic回归：当响应变量是一组有序的类别（例如信用为好，良，差）时，可使用rms包中的lrm()函数拟合序数logistic回归。

2.Poisson regression

Poisson回归对于预测变量是连续型和分类型，响应变量是计数型的模型很适用。他有两个假设条件：一是具备相同特征和同时的不同对象的人时风险时同质的，其次，当样本量越来越大时，频数的均值趋近于方差。 调用Poisson模型的公式如下：

myfit<-glm(y~x1+x2+...+xn,data=,family=possion)
1)数据准备

robust包中Breslow癫痫数据记录了治疗初期八周内，抗癫痫药物对癫痫发病数的影响。响应变量为sumY（随机化后八周内癫痫发病数），预测变量为治疗条件（Trt）、年龄（Age）和前八周内的基础癫痫发病数（Base），在这个数据集中，我们感兴趣的是药物治疗能否减少癫痫发病数。

data(breslow.dat,package = "robust")
library(ggplot2)
g1<-ggplot(breslow.dat,aes(sumY))+geom_histogram(color="lightblue",binwidth = 15)
g2<-ggplot(breslow.dat,aes(Trt,sumY))+geom_boxplot()
library(gridExtra)
grid.arrange(g1,g2,nrow=1)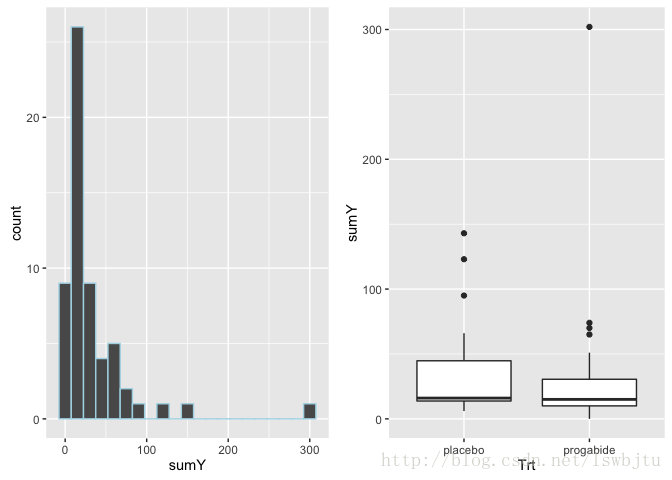

这里写图片描述
从图中可以清楚的看到因变量的偏移特性及可能的离群点。药物治疗下癫痫的发病数似乎变小，且方差也变小了。

2)构建模型
fit.Poisson<-glm(sumY~Base+Age+Trt,data=breslow.dat,family = poisson())
summary(fit.Poisson)
## 
## Call:
## glm(formula = sumY ~ Base + Age + Trt, family = poisson(), data = breslow.dat)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -6.0569  -2.0433  -0.9397   0.7929  11.0061  
## 
## Coefficients:
##                Estimate Std. Error z value Pr(>|z|)    
## (Intercept)   1.9488259  0.1356191  14.370  < 2e-16 ***
## Base          0.0226517  0.0005093  44.476  < 2e-16 ***
## Age           0.0227401  0.0040240   5.651 1.59e-08 ***
## Trtprogabide -0.1527009  0.0478051  -3.194   0.0014 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 2122.73  on 58  degrees of freedom
## Residual deviance:  559.44  on 55  degrees of freedom
## AIC: 850.71
## 
## Number of Fisher Scoring iterations: 5

结果说明治疗药物对癫痫的发病数有改善。

lswbjtu
关注
  • 1
    点赞
  • 踩
  • 9
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
5广义线性模型02.mp4
07-20
基于王斌会《多元统计分析及R语言建模》第5章。logistic模型的建立过程，分析过程，以及相关的算例。双因素方差分析的数据结构，建模和解释，以及相关的算例。
广义线性模型的matlab代码
02-09
这是一个关于广义线性模型的matlab代码，里面有说明。 (glmlab is a set of m-files for using MATLAB for analysing generalised linear models. )
全面概述：啥是广义线性模型 （GLM）？
最新发布
gongdiwudu的专栏
02-26 1460
广义线性模型 （GLM） 是一个强大的统计框架，它扩展了经典线性回归模型以处理各种数据类型和分布。1970 年代，统计学家 John Nelder 和 Robert Wedderburn 引入了 GLM，已成为从流行病学和金融学到生态学和社会科学等领域不可或缺的工具。本文全面概述了 GLM，探讨了它们的基本概念、关键组件和实际应用。
广义线性模型（陈希孺）
10-10
本讲座是2002年陈希孺先生发表在《数理统计与管理》上的系列文章合集，是广义线性模型这个题目的一个比较系统的介绍。主要分3部分：建模，统计分析与模型选择，诊断。写作时依据的主要参考资料是L. Fahrmeir等人的《Multivariate Statistical Modeling Based on Generalized Linear Models》。
广义线性模型SAS程序
09-01
本资源是用来构建广义线性回归模型的SAS程序
广义线性模型（GLM）
weixin_30843605的博客
01-29 719
一、广义线性模型概念 在讨论广义线性模型之前，先回顾一下基本线性模型，也就是线性回归。 在线性回归模型中的假设中，有两点需要提出： （1）假设因变量服从高斯分布：$Y={{\theta }^{T}}x+\xi $，其中误差项$\xi \sim N(0,{{\sigma }^{2}})$，那么因变量$Y\sim N({{\theta }^{T}}x,{{\sigma }^{2}})$。　　 ...
广义线性模型（GLMs）及算法介绍
sun_xiao_kai的博客
02-27 1万+
  一般我们了解的线性模型是针对连续性变量，并且服从正态分布的，但是在实际应用上显得非常的局限。因为我们我看到的数据很多都是离散的，而且不是服从正态分布的。针对这种情况，对传统线性模型进行推广，行成了现在的广义线性模型。广义线性模型使得变量从正态分布拓展到指数分布族，从连续型变量拓展到离散型变量，这就使得在现实中有着很好的运用，下面开始介绍广义线性模型。 ###广义线性模型（GLM）定义 由以下三...
广义线性模型（Generalized Linear Model）
weixin_44816556的博客
04-20 5363
理解广义线性模型，Softmax Regression
广义线性模型_往期精彩：广义线性模型概述
weixin_39725594的博客
12-15 4082
　　广义线性模型是一种范围更广、功能更强大的一大类模型，其组成可分为因变量、线性部分和连接函数。许多广泛应用的统计模型都可以归入其中，如一般线性模型仅是它的一个子集。因而，广义线性模型更具有普遍性，进一步扩展了一般线性模型的应用，大大扩宽了其适用范围。广义线性模型与一般线性模型区别：　　1.一般线性模型要求因变量符合正态分布，不同取值之间要相互独立，而且还要符合方差齐性。广义线性模型的因...
16 | 建模非正态分布：广义线性模型
qq_37756660的博客
10-27 498
元素的半衰期和原子的总量无关，100 个原子中衰变 50 个的时间和剩下的 50 个原子中衰变 25 个的时间是一致的。在求解时，狭义的线性模型建立在最小均方误差的意义上，其解析解可由普通最小二乘法求得，求解时的一个基本前提是因变量，也就是回归结果的误差服从正态分布。泊松分布适用于描述单位时间或空间内随机事件发生的次数，比如电话交换机接到呼叫的次数，汽车站台的候客人数，机器出现的故障数，自然灾害发生的次数等。线性模型的意义是建立了自变量和因变量的关联，当自变量变化时，因变量也会出现依照比例同等程度的变化。
广义线性模型(Generalized Linear Model)——机器学习
热门推荐
Norstc的博客
08-08 1万+
零、前言 对于条件分布(y|x;θ)，对于线性回归模型有，而对分类问题有。其实这些分布均是广义线性模型（GLM）的特殊情况。 我们通过定义广义线性模型，可以据此求出拟合函数h(x)   一、指数分布族（Exponential Family） 其定义如下 其中，η称为自然参数（natural parameter），T(y)称为充分统计量（sufficient statistic）（通...
广义线性模型_广义线性模型(GLM)从人话到鬼话连篇
weixin_39532466的博客
12-05 1376
作为一个应用者来说，要了解一个模型的顺序是：1)为什么要用这个模型解决问题？2)这个模型是什么，可以解决什么问题？3)模型怎么用？4)应用领域是什么？解决了哪些问题？5)模型的归档与应用划分？人话篇：广义线性模型到由来从逻辑回归模型开始，我们连续讲了好多集有些相似又特点各异的几种统计模型。它们有个统一的旗号，叫做「广义线性模型」(generalized linear model)。许多在...
stats | 广义线性模型（一）——广义线性模型的基本结构及与线性模型的比较...
R语言学堂
05-26 2041
前面已经介绍了线性模型，本系列将介绍广义线性模型（Generalized Linear Model，GLM）。广义线性模型的大多方法都与线性模型类似，因此本系列主要介绍它的不同之处。示例数...
广义线性模型（Generalized linear model）
weixin_42056532的博客
04-03 6476
终于，对该concept有了一个初步且较为完整的理解了！本文为学习医咖会小课堂中《广义线性模型-stata教程》记录。 对于数学原理，我没有深究，主要目的是为了理解glm是个啥？ 在广义线性模型中，相比简单线性模型，这是对因变量Y进行了变换，使变换后的Y和X呈线性关系 分类：简单广义线性回归（simple glm）；多元广义线性回归（multiple glm） 其中，X可以是各种类型的变量（连续、分类） 需要考虑的两个问题，如上图所示。平时使用的linear regression, log
广义线性模型_广义线性模型
weixin_39583013的博客
12-03 1055
1.1. 广义线性模型本章主要讲述一些用于回归的方法，其中目标值 y 是输入变量 x 的线性组合。 数学概念表示为：如果 是预测值，那么有：在整个模块中，我们定义向量 作为 coef_ ，定义 作为 intercept_ 。如果需要使用广义线性模型进行分类，请参阅 logistic 回归 。1.1.1. 普通最小二乘法LinearRegression 拟合一个带有系数 的线性模型，使得数据集实...
广义线性模型检验python
09-26
广义线性模型是一种扩展了线性模型框架的方法，可以用于分析非正态因变量。在广义线性模型中，常见的模型包括Logistic回归（用于类别型因变量）和泊松回归（用于计数型因变量）。在Python中，我们可以使用statsmodels库来进行广义线性模型的检验。 示例代码如下： ``` import statsmodels.api as sm # 准备数据 X = ... # 自变量 y = ... # 因变量 # 添加常数列到自变量矩阵中（如果需要） X = sm.add_constant(X) # 构建广义线性模型 model = sm.GLM(y, X, family=sm.families.<family_name>) # 拟合模型 result = model.fit() # 打印模型检验结果 print(result.summary()) ``` 在代码中，你需要将`<family_name>`替换为你想要使用的分布类型，例如`sm.families.Binomial()`表示使用二项分布进行Logistic回归，`sm.families.Poisson()`表示使用泊松分布进行泊松回归。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值