此处模型选择我们只考虑模型参数数量,不涉及模型结构的选择。
很多参数估计问题均采用似然函数作为目标函数,当训练数据足够多时,可以不断提高模型精度,但是以提高模型复杂度为代价的,同时带来一个机器学习中非常普遍的问题——过拟合。所以,模型选择问题在模型复杂度与模型对数据集描述能力(即似然函数)之间寻求最佳平衡。
人们提出许多信息准则,通过加入模型复杂度的惩罚项来避免过拟合问题,此处我们介绍一下常用的两个模型选择方法——赤池信息准则(Akaike Information Criterion,AIC)和贝叶斯信息准则(Bayesian Information Criterion,BIC)。
AIC是衡量统计模型拟合优良性的一种标准,由日本统计学家赤池弘次在1974年提出,它建立在熵的概念上,提供了权衡估计模型复杂度和拟合数据优良性的标准。
通常情况下,AIC定义为:
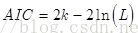
其中k是模型参数个数,L是似然函数。从一组可供选择的模型中选择最佳模型时,通常选择AIC最小的模型。
当两个模型之间存在较大差异时,差异主要体现在似然函数项,当似然函数差异不显著时,上式第一项,即模型复杂度则起作用,从而参数个数少的模型是较好的选择。
一般而言,当模型复杂度提高(k增大)时,似然函数L也会增大,从而使AIC变小,但是k过大时,似然函数增速减缓,导致AIC增大,模型过于复杂容易造成过拟合现象。目标是选取AIC最小的模型,AIC不仅要提高模型拟合度(极大似然),而且引入了惩罚项,使模型参数尽可能少,有助于降低过拟合的可能性。
BIC(Bayesian InformationCriterion)贝叶斯信息准则与AIC相似,用于模型选择,1978年由Schwarz提出。训练模型时,增加参数数量,也就是增加模型复杂度,会增大似然函数,但是也会导致过拟合现象,针对该问题,AIC和BIC均引入了与模型参数个数相关的惩罚项,BIC的惩罚项比AIC的大,考虑了样本数量,样本数量过多时,可有效防止模型精度过高造成的模型复杂度过高。
其中,k为模型参数个数,n为样本数量,L为似然函数。kln(n)惩罚项在维数过大且训练样本数据相对较少的情况下,可以有效避免出现维度灾难现象。





 本文介绍了两种常用的信息准则——AIC与BIC,在模型选择过程中如何平衡模型复杂度与数据集描述能力,避免过拟合现象。
本文介绍了两种常用的信息准则——AIC与BIC,在模型选择过程中如何平衡模型复杂度与数据集描述能力,避免过拟合现象。
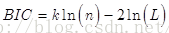
















 1504
1504

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








