Logistic回归为概率型非线性回归模型,是研究二分类观察结果
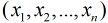
变量分析方法。通常的问题是,研究某些因素条件下某个结果是否发生,比如医学中根据病人的一些症状来判断它是
否患有某种病。
在讲解Logistic回归理论之前,我们先从LR分类器说起。LR分类器,即Logistic Regression Classifier。
在分类情形下,经过学习后的LR分类器是一组权值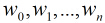
照线性加和得到
这里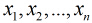
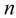
之后按照sigmoid函数的形式求出
由于sigmoid函数的定义域为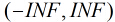
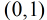
所以Logistic回归最关键的问题就是研究如何求得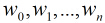
下面正式地来讲Logistic回归模型。
考虑具有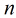
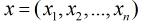
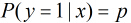
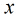
概率。那么Logistic回归模型可以表示为
这里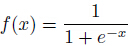
那么在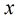

所以事件发生与不发生的概率之比为
这个比值称为事件的发生比(the odds of experiencing an event),简记为odds。
对odds取对数得到
可以看出Logistic回归都是围绕一个Logistic函数来展开的。接下来就讲如何用极大似然估计求分类器的参数。
假设有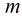
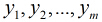
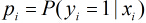
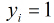
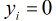
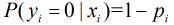
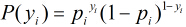
因为各个观测样本之间相互独立,那么它们的联合分布为各边缘分布的乘积。得到似然函数为
然后我们的目标是求出使这一似然函数的值最大的参数估计,最大似然估计就是求出参数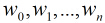
取得最大值,对函数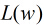
继续对这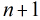
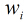
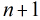
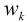
所以得到
这样的方程一共有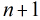
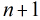
上述方程比较复杂,一般方法似乎不能解之,所以我们引用了牛顿-拉菲森迭代方法求解。
利用牛顿迭代求多元函数的最值问题以后再讲。。。
简单牛顿迭代法:http://zh.m.wikipedia.org/wiki/%E7%89%9B%E9%A1%BF%E6%B3%95
实际上在上述似然函数求最大值时,可以用梯度上升算法,一直迭代下去。梯度上升算法和牛顿迭代相比,收敛速度
慢,因为梯度上升算法是一阶收敛,而牛顿迭代属于二阶收敛。
转自:
http://blog.csdn.net/ariessurfer/article/details/41310525








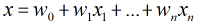
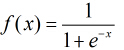
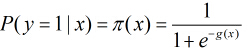
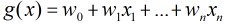
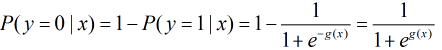
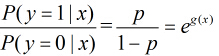
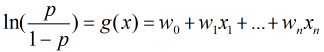
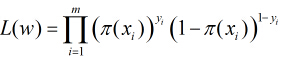
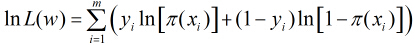
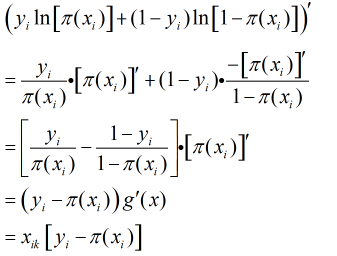
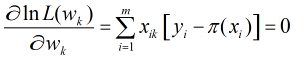













 2493
2493











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








