一、拜占庭问题的背景这里就不再介绍直接说算法:
下面的这个截图是从Lamport发表的论文中截取的:
对于这个算法需要说明的是:
(1) 在第一轮 将军会把消息发送给所有的副官,第i个副官收到的记为 Vi。如 1(这里代表的是Attack)
(2) 在第二轮里面,Li(即第i个副官)会怀疑将军发来的消息Vi是对还是错,于是他会问其余的副官。这样他就会得到剩下的(n-2)个副官的值。 i从1到n-1,所以每个副官都会得到剩余的n-2个副官手里的Vi。在这一步骤里,忠诚的副官j会直接将自己的 Vj发送给其它人。叛徒则会发假消息。
在n=7,m=2的时候 如果将军是忠臣的话,那么在第二轮忠诚的副官确实已经可以判断出要做的决定,因为他们会收到(1 1 1 0 0 )再加上将军发来的1就是 1 1 1 1 0 0 但是这个算法是递归的所有必须要到第三轮。并且如果将军是个叛徒的话,那么第二轮有情形是做不出决定的。
这里对进入第三轮的解释是,如L1收到其它L2~L6发来的Vj, 但是他要怀疑准确性,比如L1会想L2发给自己是否是正确的呢?那么就进入第三轮进行投票。
(3)在第三轮里面,接着(2)中后面的问题。L1会依次询问L3,4,5,6 ,问他们上一轮L2给他们发了什么,然后L1会得到在(2)中 L2->L3, L2->L4,L2->L5, L2->L6的值 这样再结合自己的L2->L1的值,从这5个里面用majority函数投出决定得到L2发给自己的消息值。依次再进行L3,L4,L5,L6在第二轮中发给自己的消息的确认。
这样L1就完成了第二轮的确认。之后L1再从第一步中将军发给自己的vi和第二轮中确定的5个值中投出自己的决定。
其余的L2,L3.等等也进行同样的步骤。
二、好像算法是挺绕的,如果还是没清晰的话,直接看下面的过程:
这里需要注意的是:Lamport提出的容错的两个条件
IC1:即所有的忠诚的副官要遵守同一个命令,即达成一致;
IC2:假如将军是忠诚的,那么每一个忠诚的副官都应该按照将军的意思行事。
这里将军是叛徒,所以只要满足IC1条件即可。
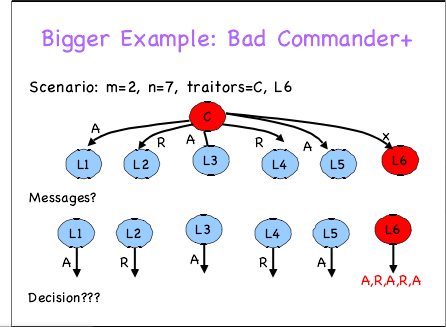
Step1 : C给L1~L6 依次发 A R A R A x (A,R代表攻击和撤退,这里因为C是叛徒,所以可以随便发给L1-L5消息,这里只是一个例子,可以用其他的值,只要最后满足IC1就可以)
截图是Step2:
Step3:其实在第三步中 L1会依次确认在step2中, L2~L6发给自己的信息. 例如确认L2时 会问L3-L6,在Step2中L2发给你们了什么
最后得到 R, R, R,X (因为L6这时候肯定又说谎) 再结合自己的R , L1确定在Step2中收到L2发来的是R,之后又确认了L3-L6。大家可以自己在草稿纸上画出。
其实因为L1-L5都是忠诚,他们不会在Step2中撒谎,所以只需投票L6即可 ,(A R A R A )是L6发给L1-L5的信息,最后投出发的是A , 将A修改到step2中L1-L5收到的
信息中其余的信息可以不用改。
最后得到L1-L5均是 4个A, 2个R。 以L1为例=R A R A A A
即L1~L5达成了一致。
三、下面来看签名时候的情形:(详细的关于签名的算法见下一篇博客)
在lamport的论文中提到:
签名就是说每次发送信息都要签署上自己的名字,然后再发给别人。而别人只可以在这条消息上复制然后再转发出去。这样就变的简单了,
而且
1)忠诚司令的签名不可伪造,内容修改可以被检测出来。
2)任何人都可以识别司令的签名,叛徒可以伪造叛徒司令的签名。
http://blog.csdn.net/michael_kong_nju/article/details/17612969 (详细介绍签名算法)
四、下面来看相关的证明。
证明1: 为什么在没有签名的情况下,n>3m即可容错?
在Lamport的论文中,在证明OM(m)在最多只有m个叛徒,以及超过3m个将军的时候可以满足IC(1)和IC(2)条件的时候,先引入了一个引理:
LEMMA1:对于 任意m 和k ,如果有超过2k+m 个将军和最多k 个背叛者,那么算法OM(m) 满足IC2 (回顾下IC2 指的是,如果将军是忠诚的,所有的副官遵守将军命令)。证明:(1)当m=0的时候,如果将军是忠诚的,因为在OM(0)的时候忠臣会遵守将军发来的命令。而此时的将军是忠臣的所以,即满足IC2
(2)当m>0的时候。用数学归纳法,通过证明OM(m-1)有效来证明。因为假设了n>2k+m,在OM(m-1)时剩余的将军数是n-1,但是叛徒数仍然是k(因为上1轮中的将军是忠臣),n>2k+m -> n-1>2k+m-1. 又m-1>=0 -> n-1>2k. 即在OM(m-1)中有忠诚的副官比叛徒多,所以可以投票得出正确结果。在O(m-1)时可证。
接着证明“证明1”中的问题:
证明:通过m的归纳法证明,我们通过假设OM(m-1) 成立来证明OM(m) m>0。
(1)首先考虑发送命令的将军是忠诚的。那么将引理中k 设为m 则OM(m) 满足IC2 ,IC1 在发令将军是忠诚的情况下也满足。
(2)如果发送命令的将军是叛徒。那么在下一轮中,总共有3m个副官,其中有m-1个副官是叛徒,有3m-(m-1)=2m+1个忠臣,
2m+1>m-1 即 在这里所有的忠臣是可以达成一致的(这一步是为了说明OM(m-1)是成立的)。下面再推出OM(m-1)的表达式:这里除去要发送命令的一个将军外还有超过3m-1个,有3m-1>3(m-1) 即 n'>3m',所以在OM(m-1)是满足条件的,得证。
在这里也同时证明了为什么是m+1轮交换。因为OM(m)满足。m->0 共 m+1;
























 3555
3555











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








