【数论】codeforce711E ZS and The Birthday Paradox

题目大意：

给n和k。

求2^n天，k个人，其中至少两人同一天生日的概率。

1 ≤ n ≤ 1018, 2 ≤ k ≤ 1018

输出分子和分母 MOD 1e6+3

求MOD前，要求分子分母互质。

题解：

看到题就蒙了，主要搬运官解。

要用到勒让德公式

p是质数，n是非负整数， 是n中不超过n的p^x的最大的x值。 表示向下取整。

  令 为n的p进制中所有位数字的和。则有：

由于要求分子分母求MOD前互质，我们还需要求出分子分母的GCD。

概率公式比较好求。

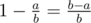  要求的概率是这个

 由于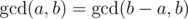，可以直接求a与b的GCD。

分母明显是2的幂次，故gcd一定是2的幂次，这里就用到了勒让德公式。

求出(2n - 1)(2n - 2)...(2n - (k - 1))这个式子中2的最大幂次，就相当于求出了gcd。

而这个式子的最大幂次相当于分别求出2n - 1； 2n - 2； ..., 2n - (k - 1)；的最大幂次并对他们的幂次求和。

神奇的来了，如果x中2的最大幂次为q且不超过n,那么2n - x中2的最大幂次仍然是q（提出2^q，显然）

所以(2n - 1)(2n - 2)...(2n - (k - 1))变成了(k - 1)! 

这是个裸的勒让德公式了。而求2进制位数和是个 .

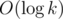分母本身就很好求，重点在于分子的部分。

更神奇的来了，

由于(2n - 1)(2n - 2)...(2n - (k - 1))这一串数是连续的，如果超过了MOD个，那么其中肯定有一个是MOD的倍数，结果是0。

如果没超过，那么复杂度最多是O(MOD)。

这样我们分子分母都求出来了。

注：

当我们计算（k-1）*n时可能会超long long，可以先算 2k - 1，再算它的n次幂。

题解中直接减去了公共gcd的幂次，因此没有超。

代码如下

#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
#define MOD 1000003

typedef long long ll;

ll multipow(ll x, ll n, ll mod)
{
	ll ans = 1;
    while(n)
    {
		if(n&1) ans = (ans*x)%mod;
		x = (x*x)%mod;
		n>>=1;
	}
    return ans;
}

int main()
{

    ll n, k;
    cin>>n>>k;

//LL足以保存10^18 即k ；LL为63位
//处理更大的k时会出错。
	if(n <= 63 && k > (1LL<<n))
	{
		cout << 1 << " " << 1;
		return 0;
	}

	ll Le_v = 0;
	int digits = __builtin_popcountll(k - 1);
	Le_v = k - 1 - digits;
    //勒让德公式

	ll ntmp = n % (MOD - 1);
	if(ntmp < 0) ntmp += (MOD - 1);

	ll ktmp = k % (MOD - 1);
	if(ktmp < 0) ktmp += (MOD - 1);

	ll Le_vt = Le_v % (MOD - 1);
	if(Le_vt < 0) Le_vt += (MOD - 1);

    //减去分子分母的gcd
	ll exponent = ntmp*(ktmp - 1) - Le_vt;
	exponent %= (MOD - 1);
	if(exponent < 0) exponent += MOD - 1;

//分母
	ll deno = multipow(2, exponent,MOD);

//分子
	ll numpart = 0;
	if(k - 1 >= MOD)
	{
		numpart = 0;
	}


	else
	{
		ll gcd = 1;
		ll ntmp2 = multipow(2, ntmp,MOD);

        gcd = multipow(2, Le_vt,MOD);
//      cout<<"pa "<<gcd<<endl;
		gcd = multipow(gcd, MOD - 2,MOD);//相当于对计算结果除以gcd
//		cout<<"p "<<gcd<<endl;

		if(gcd < 0) gcd += MOD;

		for(ll y = 1; y <= k - 1; y++)
		{
			gcd = (gcd * (ntmp2 - y))%MOD;
		}
//cout<<"pb"<<gcd<<endl;
		numpart = gcd;
	}

	ll num = (deno - numpart)%MOD;
	num %= MOD; deno %= MOD;
	if(num < 0) num += MOD;
	if(deno < 0) deno += MOD;

    cout << num << " " << deno<<endl;

	return 0;
}