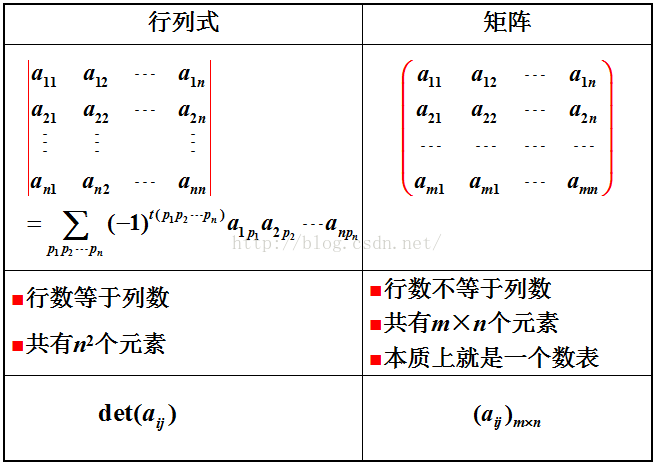
1. 行列式
1.1 二阶行列式
1.2 三阶行列式
1.3 排列的逆序数
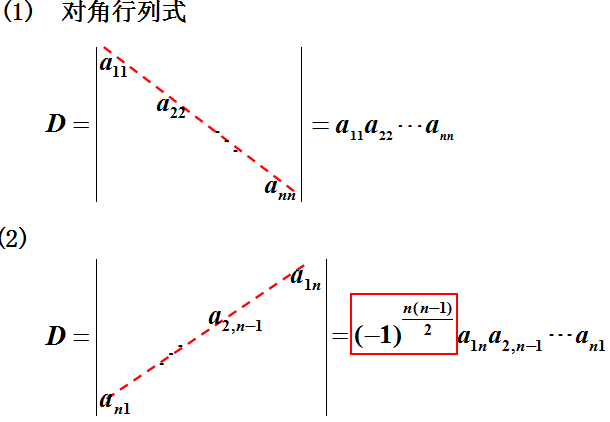
1.4 n阶行列式
2. 行列式的性质
性质1 行列式与它的转置行列式相等。
性质2 互换行列式的两行(列),行列式变号。
性质3 行列式的某一行(列)中所有的元素都乘以同一个倍数K,等于用数K乘以此行列式。
性质4 行列式中如果有两行(列)元素成比例,则此行列式为零。
行列式中行与列具有同等的地位, 凡是对行成立的性质对列也同样成立.
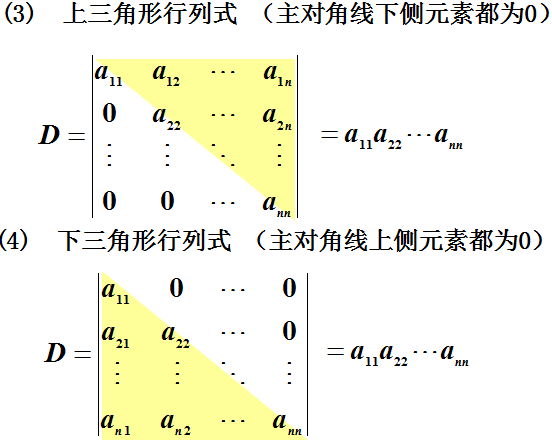
计算行列式常用方法:(1)利用定义;(2)利用性质把行列式化为上三角形行列式,从而算得行列式的值.
3. 求解方程组
3.1 克拉默法则
定理4 如果线性方程组的系数行列式不等于零,则该线性方程组一定有解,而且解是唯一的 .
定理4′ 如果线性方程组无解或有两个不同的解,则它的系数行列式必为零.
4. 矩阵
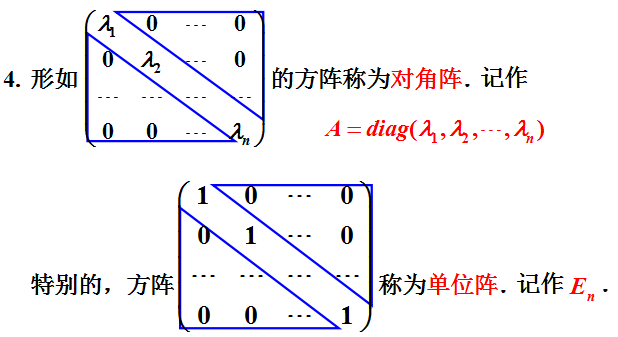
4.1 特殊矩阵
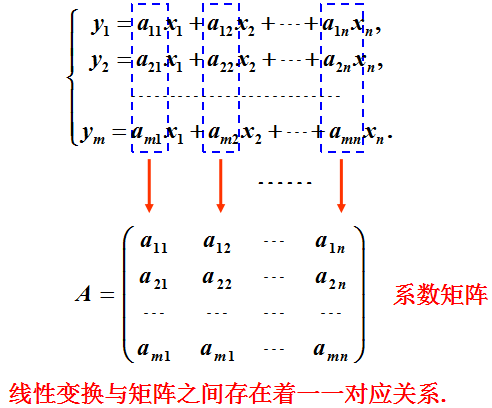
4.2 矩阵与线性变换
4.3 矩阵的运算
4.3.1 矩阵的加法
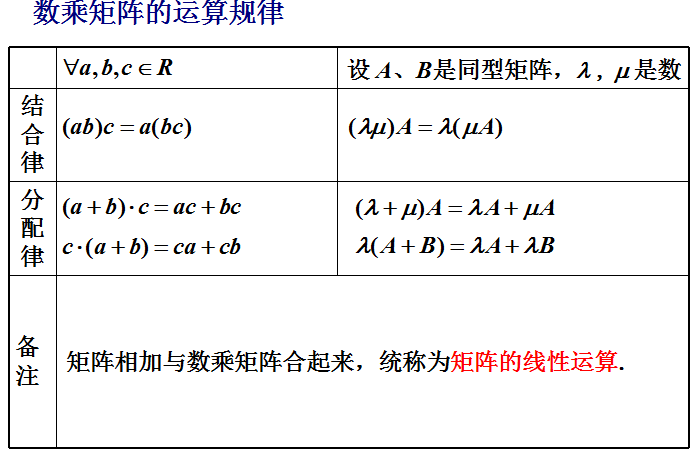
4.3.2 数与矩阵相乘
4.3.3 矩阵与矩阵相乘
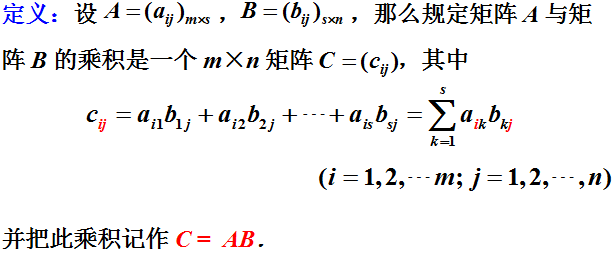
4.3.4 矩阵的转置
4.3.5 方阵的行列式
5. 范数
范数,是具有“长度”概念的函数。
5.1 向量范数



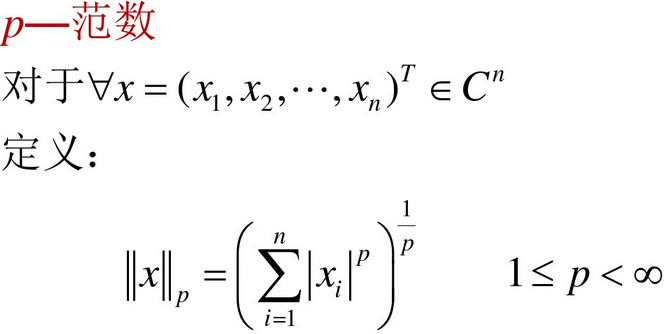
5.2 矩阵范数
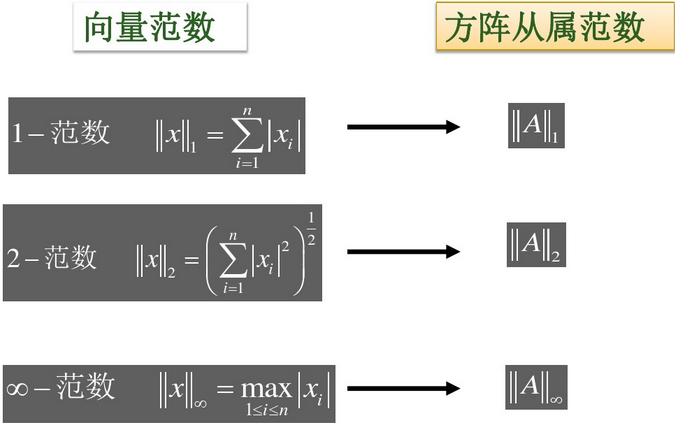
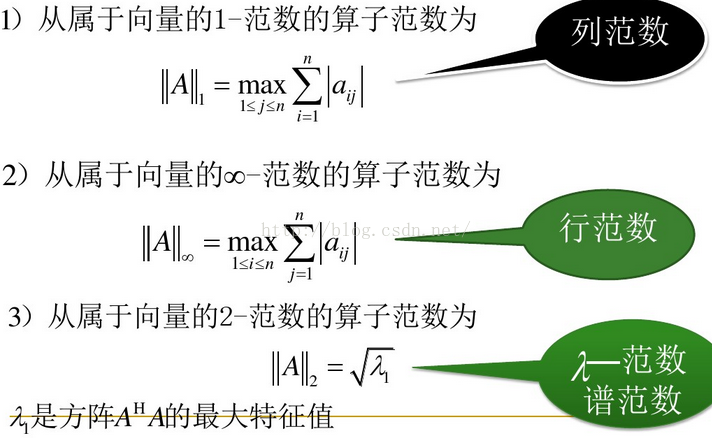
矩阵范数反映了线性映射把一个向量映射为另一个向量,向量的“长度”缩放的比例。
范数理论是矩阵分析的基础,度量向量之间的距离、求极限等都会用到范数,范数还在机器学习、模式识别领域有着广泛的应用。
理论上讲范数的概念属于赋范线性空间,最重要的作用是诱导出距离,进而还可以研究收敛性.
一个集合(向量),通过一种映射关系(矩阵),得到另外一个集合(另外一个向量),则:
1) 向量的范数:就是表示这个原有集合的大小。
2) 矩阵的范数:就是表示这个变化过程的大小的一个度量。
计算机领域:用的比较多的就是迭代过程中收敛性质的判断,一般迭代前后步骤的差值的范数表示其大小,常用的是二范数,差值越小表示越逼近实际值,可以认为达到要求的精度,收敛。
6. 向量的内积








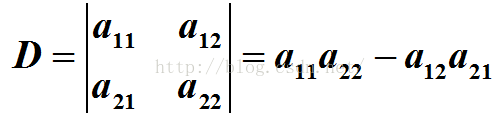
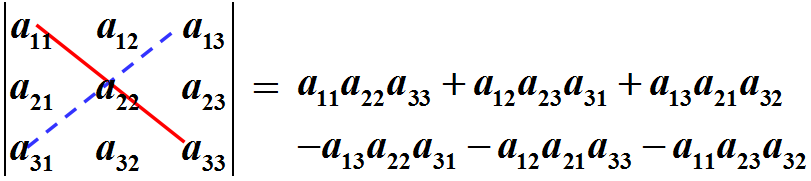













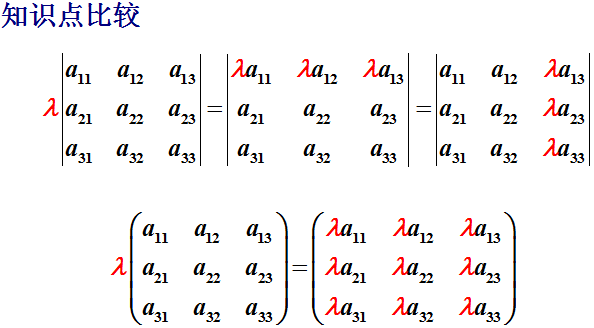






















 676
676











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








