1. 基本概念
- 视觉惯性:Visual-Inertial (VI)
- VI ORB-SLAM:视觉惯性ORB-SLAM
- VI ORB-SLAM输入:
- IMU数据(用B表示,加速度: aB;角速度:ωB ;时间间隔: △t )
- 单目图像
- 在图像中提取KeyPoints时,对像素坐标进行畸变校正,即此KeyPoint坐标可与投影点坐标进行匹配
- IMU数据(加速度和角速度)的测量除了被传感器噪声影响之外,还被缓慢变化的加速度(Accelerometer)偏差( ba )和陀螺仪(Gyroscope)偏差( bg )
- 加速度:受重力加速度( gw )影响,所在在计算运动时,需要减去重力加速度的作用。
- SO(3) :The group of rotations about the origin in 3 dimensions
- SE(3) :The group of rigid body motions (comprising rotations and translations) in 3 dimensions
2. 向量
- 向量的运处可以由坐标运算来表达;下面的a、b都为列向量。
2.1 向量加减法
2.2 向量内积/点乘(结果为实数)
2.3 向量外积/叉乘(结果为向量)
2.4 向量欧氏长度(向量2范数)
- x :为列向量
||x|| :向量欧氏长度(向量2范数)- ||x||=(xTx)1/2
3. 特殊矩阵
3.1 旋转矩阵 (特殊正交群)
- R是一个正交矩阵( RRT=I )
- R的行列式为+1 (
det(A)=+1
)
SO(n)={R∈Rn×n|RRT=I,det(A)=1}
3.2 对称矩阵 (Symmetric Matrix)
- 对称矩阵: A=AT
- 若A是实对称矩阵,则有:
A=UDUT
- U:正交矩阵
- D:实对角矩阵
- 实对称矩阵:有实特征值;且特征向量正交
- 提取实对称矩阵的特征值:雅可比方法(Jacobi′smethod)
3.3 反对称矩阵 (Skew-Symmetric Matrix)
- 反对称矩阵: A=−AT
- 若S是实反对称矩阵,则有:
S=UBUT
- B:块对角矩阵,其形式为:
diag(a1Z,a2Z,...,amZ,0,...,0),whereZ=[0−110] - S的特征向量都是纯虚数,奇数阶的反对称矩阵是奇异的(不可逆)
- B:块对角矩阵,其形式为:
-
向量的反对称矩阵
:若
a=(a1,a2,a3)T
是一个3维列向量, 其反对称矩阵为:
[a]×=⎡⎣⎢0a3−a2−a30a1a2−a10⎤⎦⎥
-
a
:是
3×1 的列向量 - [a]× :是 3×3 的反对称矩阵
- 矩阵 [a]× :是奇异矩阵(不可逆)
-
a
:是
- 向量叉乘与反对称矩阵的关系:
a×b=a∧b=⎡⎣⎢ia1b1ja2b2ka3b3⎤⎦⎥=⎡⎣⎢a2b3−a3b2a3b1−a1b3a1b2−a2b1⎤⎦⎥=⎡⎣⎢0a3−a2−a30a1a2−a10⎤⎦⎥b=[a]×b=(aT[b]×)T
4. 3D坐标系
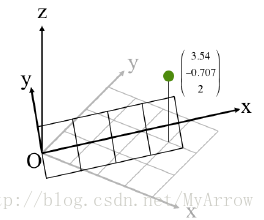
4.1 坐标系旋转
- 灰色的为坐标系1 (
V1=(322)T
),黑色的为坐标系2 (
V2=(3.54−0.7072)T
$)
- 坐标系2的x轴和y轴相对于坐标系1有旋转,其旋转矩阵为:
R=⎡⎣⎢0.707−0.70700.7070.7070001⎤⎦⎥
旋转矩阵 R 的直观理解:
R 的列对应于单位向量- 此单位向量的的值为坐标系1的对应轴的单位向量在坐标系2中值
-
R
的第一列:为坐标系1中点
(100)T 在坐标系2中的值 -
R
的第二列:为坐标系1中点
(010)T 在坐标系2中的值 -
R
的第三列:为坐标系1中点
(001)T 在坐标系2中的值
只有满足以下要求的 3×3 矩阵( R )才能表示坐标轴旋转:
- R的列向量的长度(2-范数)都为1
- R的列向量相互正交(即内积为0)
- R的行列式为1(
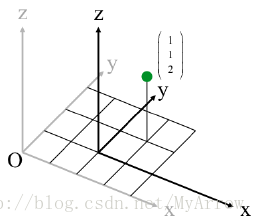
detA=1 ) 4.2 坐标系平移
- 灰色的为坐标系1 (
V1=(322)T
),黑色的为坐标系2 (
V2=(112)T
-
V2=V1+t
:
t
为坐标系1的原点在坐标系2中的位置
(−2−10)T
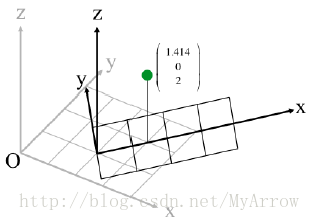
4.3 坐标系旋转与平移的组合
- 灰色的为坐标系1 (
V1=(322)T
),黑色的为坐标系2 (
V2=(1.41402)T
R=⎡⎣⎢0.707−0.70700.7070.7070001⎤⎦⎥,t=⎡⎣⎢−2.1210.7070⎤⎦⎥V2=RV1+t
4.4 齐次坐标系
- 上面的旋转和平移需要用一个方程来表示: V2=RV1+t
- 坐标系的旋转和平移能否用一个矩阵来表示呢?
-
齐次坐标系
:可把坐标系的旋转和平移用一个矩阵来表示
T4×4=[R3×301×3t3×111×1]T−14×4=[RT3×301×3−RT3×3t3×111×1]⎡⎣⎢⎢⎢0.707−0.707000.7070.707000010−2.1210.70701⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢3221⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢1.414021⎤⎦⎥⎥⎥
5. 李群与李代数(Lie Group and Lie Algebra)
5.1 引入李群与李代数的原因
- 三维世界刚体运动的描述: 旋转矩阵、旋转向量、欧拉角、四元数等
- 除了 表示 之外, 还需要对其进行 优化 和 估计
- 旋转矩阵自身带有约束( 正交且行列式为1 ),作为优化变量时,会引入额外的约束,使优化变得困难
- 李代数上可以变为 无约束优化
5.2 特殊正交群与特殊欧氏群
- 三维旋转矩阵构成了
特殊正交群(SpecialOrthogonalgroup)
SO(3)={R∈R3×3|RRT=I,det(R)=1} - 三维变换矩阵(旋转+平移)构成了
特殊欧氏群(SpecialEuclideangroup)欧氏意为刚体变换
SE(3)={T=[R0Tt1]∈R4×4|R∈SO(3),t∈R3} - 群(Group):是一种集合(
A
)加上一种运算的代数结构,此运算满足以下性质(凤姐咬你):
- 封闭性:
∀a1,a2∈A,a1⋅a2∈A - 结合律: ∀a1,a2,a3∈A,(a1⋅a2)⋅a3=a1⋅(a2⋅a3)
- 幺元: ∃a0∈A,s.t.∀a∈A,a0⋅a=a⋅a0=a
- 逆: ∀a∈A,∃a−1∈A,s.t.a⋅a−1=a0
- 封闭性:
- 旋转矩阵集合+矩阵乘法:构成群(旋转矩阵群: SO(3) (3维特殊正交群))
- 变换矩阵集合+矩阵乘法:构成群(变换矩阵群: SE(3) (3维特殊欧氏群))
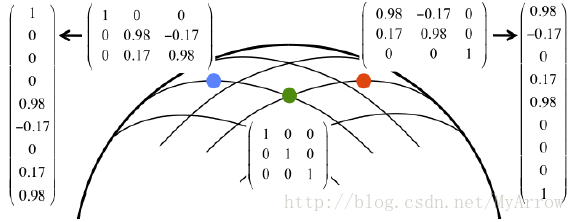
5.3 李群(Lie Group)(位于矩阵空间)
- 李群( SO(3) ):三维空间旋转矩阵的集合
李群中的旋转矩阵有9个值,所以可以把 SO(3) 看作9维空间
- 上图是SO(3)表面(流形)(surface (manifold))的一部分
- 绿点:表示单位矩阵
- 蓝点:绕 x 轴旋转了10度
- 红点:绕
z 轴旋转了10度
在 SO(3) 中,如何表示单位矩阵附近的R矩阵?
R=⎡⎣⎢1−b−cb1−fcf1⎤⎦⎥- b,c,f :无穷小
- 此矩阵有3个参数,因此在单位矩阵附近的矩阵看起来像一个三维空间
- 此矩阵的来由:
- 把R表示为在单位矩阵附近的形式:
R=⎡⎣⎢100010001⎤⎦⎥−f⎡⎣⎢0000010−10⎤⎦⎥+c⎡⎣⎢00−1000100⎤⎦⎥−b⎡⎣⎢010−100000⎤⎦⎥ - 设
α1=−f,α2=c,α3=−b
,则有:
R=I+α1G1+α2G2+α3G3(α1,α2,α3都无穷小)G1=⎡⎣⎢0000010−10⎤⎦⎥G2=⎡⎣⎢00−1000100⎤⎦⎥G3=⎡⎣⎢010−100000⎤⎦⎥
G1,G2,G3 :叫做单位矩阵附近矩阵的导数分量,即生成矩阵(Generator Matrices)。
李群的性质:
- 具有连续(光滑)性质的群
- 既是群,也是流形
- 直观上看,一个刚体能够连续地在空间中运动,所以 SO(3) 和 SE(3) 都是李群
- 局限性:李群只定义了良好的乘法,而没有加法,所以无法进行求极限、求导等操作 ,即无法进行优化
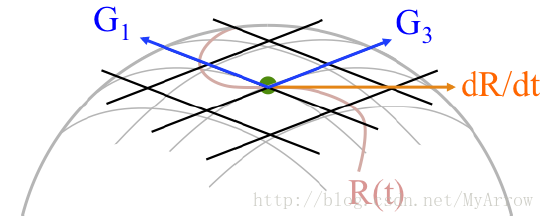
5.4 正切空间和导数:李代数(Lie Algebra)(位于向量空间)
- 正切空间:是一个向量空间,其原点在单位矩阵(identitymatrix)的位置处
- 向量空间+双线性运算 = 李代数 (Lie algebra)
- 生成矩阵(Generator Matrices( G1、G2、G3 )):是此向量空间的基
- 若
G1,G2,G3
变为非无穷小,则它们创建了一个3维平面,此平面与
SO(3)
正切于单位向量,下图是一个二维表示:
- 红色 R(t) :表示流形表面上的路径
- 橙色 dR/dt :表示当它经过单位向量时,此路径对变量t的导数
- 正切空间:可看作 SO(3) 在单位向量处可能的导数集合
- 重点:若旋转矩阵R是变量
t
(如:弧度)的函数,则当
t 取一定的值时 R(t)=I (如绿点处),在此点 dR/dt 必然位于正切空间上,且是生成矩阵( G1、G2、G3 )的线性组合:
dRdt∣R=I=∑i3αiGi 举例说明:若变量t是绕x轴旋转的弧度值,则有:
R=⎡⎣⎢1000cos(t)sin(t)0−sin(t)cos(t)⎤⎦⎥-
R
对
t 的导数为:
dRdt=⎡⎣⎢0000−sin(t)cos(t)0−cos(t)−sin(t)⎤⎦⎥ - 当t=0时,R=I,则导数为:
dRdt|t=0=⎡⎣⎢0000010−10⎤⎦⎥=G1 - G1 :对应绕 x 轴的旋转
- G2 :对应绕 y 轴的旋转
- G3 :对应绕 z 轴的旋转
-
R
对
李代数:与李群对应的一种结构,位于向量空间。
- 记作: so(3)、se(3)
- 李代数是李群单位矩阵处的正切空间
- 李代数的定义:
- 向量空间+双线性运算(特殊:三维向量+叉乘运算:构成了李代数)
- 组成:向量集合V + 数域F + 二元运算符[ , ] (叫做李括号,表示两个元素的差异)
- 李代数的通用性质:
- 封闭性: ∀X,Y∈V,[X,Y]∈V
- 双线性: ∀X,Y,Z∈V,a,b∈F则有:[aX+bY,Z]=a[X,Z]+b[Y,Z][Z,aX+bY]=a[Z,X]+b[Z,Y]
- 自反性: ∀XinV,[X,X]=0
- 雅可比恒等式: ∀X,Y,ZinV,[X,[Y,Z]]+[Y,[Z,X]]+[Z,[X,Y]]=0
- 李括号具有反对称性(anit-symmetric): ∀X,YinV,[X,Y]=−[Y,X]
- so(3)的性质(旋转向量):
- so(3)={r∈R3,S=[r]×∈R3×3}S=[r]×=⎡⎣⎢0r3−r2−r30r1r2−r10⎤⎦⎥
- se(3)的性质(刚体变换:旋转+平移向量)
- se(3)={e=[tr]∈R6,t∈R3,r∈so(3),[e]×=[[r]×0Tt0]∈R4×4}
- se(3)组成:3个平移分量+3个旋转分量
- 其旋转分量与so(3)相同
- 平移是普通的向量,但不是SE(3)上的平移分量
- [e]× 不是反对称矩阵,只是保留了相同的记法
- 把李代数理解为向量形式或矩阵形式都可以,但向量形式更加自然些
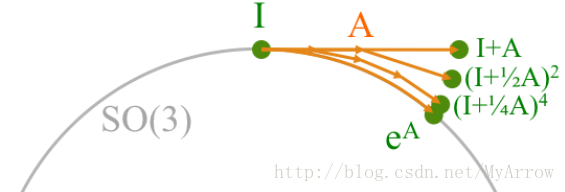
5.5 指数映射
- 设
A
是生成矩阵(导数分量)的线性组合(很明显,
A 为反对称矩阵):
A=∑i=03αiGi -
ex
的泰勒展开式:
ex=1+x+12x2+16x3+⋅⋅⋅+1n!xn -
eA
泰勒展开式:
M=eA=I+A+12A2+16A3+⋅⋅⋅+1n!An
- M以这种方式计算,它必定是 SO(3) 的成员,即M为一个旋转矩阵
- 任何SO(3)中的成员,都能以这种方式进行计算
- 为什么
M=eA
必定是
SO(3)
的成员?
eA=limn→∞(I+1nA)n
- 当n无穷大时, 1nA 变为无穷小,因此 I+1nA 成为 SO(3) 的成员(
- 因为: R=I+α1G1+α2G2+α3G3(α1,α2,α3都无穷小)
- 次数越高,
eA
越接近R,如下图所示:
- 举例说明:
- 结论:
- 指数映射:建立了在单位矩阵处的导数(如速度)与群
(SO(3)或SE(3))
成员间的关系,它可以不同的方程进行表示:
A=∑iαiGi(表示在单位矩阵处的速度)dRdt=ARR(0)=IR(t)=etAR(1)=eA
- 指数映射:建立了在单位矩阵处的导数(如速度)与群
(SO(3)或SE(3))
成员间的关系,它可以不同的方程进行表示:
-
dRdt=AR
的由来:
- 任意旋转矩阵满足:
RRT=I - 考虑R随着时间变化:
R(t)R(t)T=I - 两侧对时间求导:
dRdtR(t)T+R(t)(dRdt)T=0 - 整理得:
dRdtR(t)T=−((dRdt)R(t)T)T - 可以看出这是一个反对称矩阵,记:
dRdtR(t)T=A - 两侧右乘R(t),得:
dRdt=AR - 可以看到,对R(t)求导后,左侧多出一个反对称矩阵A
A=⎡⎣⎢0a3−a2−a30a1a2−a10⎤⎦⎥
- 任意旋转矩阵满足:
5.6 SO(3)的生成与叉乘(Corss Product
v1×v2=⎡⎣⎢abc⎤⎦⎥×⎡⎣⎢def⎤⎦⎥=[a]×b=⎡⎣⎢0c−b−c0ab−a0⎤⎦⎥⎡⎣⎢def⎤⎦⎥=⎡⎣⎢bf−cecd−afae−bd⎤⎦⎥
[a]×=⎡⎣⎢0c−b−c0ab−a0⎤⎦⎥=aG1+bG2+cG3
- 这意味着 SO(3) 中旋转矩阵可表示为: R=e[V]×
- 其参数为向量
V
中的元素,这3个参数在向量
V 与旋转矩阵 R 间建立了一个漂亮的关系 - 基于此,旋转矩阵的直观理解:
- 旋转轴:此旋转以向量
V 为旋转轴 - 旋转角度:为向量 V 的长度
- 旋转方向:沿着向量方向看,顺时针方向;沿着向量相反的方向看,逆时针方向;当
V=0 时,无旋转轴, 且旋转角度为0,即没有旋转
- 旋转轴:此旋转以向量
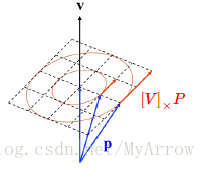
-
V与R
的关系的直观解释:
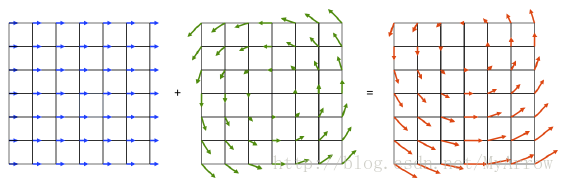
- [V]× :是在单位矩阵处的导数(即: dRdt|R=I=A=∑3iαiGi=[V]× ),且在单位时间后产生了旋转 R
[V]× :可被解释为产生一个速度向量域(velocity vector field),在空间的每一个点有一个速度向量(velocity vector)- 点P处的向量域(vector field):被定义为: [V]×P
- 在旋转轴
V
上的点没有速度,因为
V×V=0 - 在旋转轴
V
外的点有速度,它与向量
V 的长度与 [V]×P 的长度成正比 - 速度域如下图所示(由
[V]×
建立的速度域形成一个围绕V的圆形旋转)
5.7 SE(3)的生成
- SE(3)表示欧拉变换(刚体变换),在三给空间中形成了6维流形
- 它有3个平移生成矩阵和3个旋转生成矩阵
- G1,G2,G3 :分别为沿x,y,z方向的平移生成矩阵
- G4,G5,G6 :分别为绕x,y,z轴旋转的旋转生成矩阵
- 沿x方向的平移+绕z轴的旋转=沿y方向移动旋转中心
5.8 李括号(Lie bracket)
- 李代数:在群的单位矩阵处的正切空间中的向量
- 李括号:李括号=李代数+双线性反对称运算
- 指数映射:把正切空间->(映射到)群中的元素,这样可以抓住群的局部结构
-
矩阵A、B
为正切空间中的矩阵(如为生成矩阵的线性组合),则有:
eAeB≠eBeA⇒AB≠BA -
AB
与
BA
的差异叫做Commutator(换位子),即李括号, 表示为[A, B]:
[A,B]=AB−BA - 李括号是反对称的:
[A,B]=−[B,A] - 生成矩阵间的关系:
[G2,G1]=−[G1,G2]=−G3[G3,G1]=G2[G2,G3]=G1
5.9 李代数求导与扰动模型
- 在SLAM实际应用中,需要对位姿进行估计
- 李群上只有乘法,没有加法,从而无从定义导数
- 能否利用李代数上的加法,定义李群元素的导数?基本问题是:当在李代数中做加法时,是否等价于在李群上做乘法:
eA1eA2=eA1+A2:此等式当 A1、A2 为矩阵时,成立吗? - 根据BCH线性近似,可得:
1)左乘雅可比:
Jl=J=sinθθI+(1−sinθθ)aaT+1−cosθθ[a]×
J−1l=θ2cosθ2I+(1−θ2cosθ2)aaT−θ2[a]×2)右乘雅可比:
Jr(v)=Jl(−v)
3)在李群上左乘小量时,李代数上的加法相差左雅可比的逆:
e[△v]×e[v]×=e[v+J−1l(v)△v]×
4)李代数上进行小量加法时, 相当于李群上左乘一个带左雅可比的量,或右乘一个带右雅可比的量
e[v+△v]×=e[Jl△v]×e[v]×=e[v]×e[Jr△v]×
- 通过BCH线性近似,可以定义李代数上的导数
- 旋转后的点关于旋转的导数,不严谨地记为 :
∂(Rp)∂R
- 由于R没有加法,导数无法定义
- 存在两种解决办法
- R对应的李代数上加上小量,求相对于小量的变化率( 导数模型)
- 对R左乘或右乘一个小量,求相对于小量的李代数的变化率(扰动模型)
- 导数模型
- 按照定义可得:
∂(Rp)∂R=∂(e[v]×p)∂v=lim△v→0e[v+△v]×p−e[v]×p△v=−[Rp]×Jl
- 结果中含有左乘雅可比,比较复杂
- 扰动模型
- 左乘小量,令其李代数为0
∂(Rp)∂△v=lim△v→0e[△v]×e[v]×p−e[v]×p△v≈lim△v→0(1+[△v]×)e[v]×p−e[v]×p△v=lim△v→0[△v]×Rp△v=lim△v→0−[Rp]×△v△v=−[Rp]×
- 最终结果更为简洁,所以更实用5.10 总结
反对称矩阵⟺三维向量 :
- 由于 AT=−A ,所以它主对角线元素必为0,而非对角线元素则只有三个自由度。
- 可以把反对称矩阵对应到一个三维向量
- 用途:它与叉积兼容,可以直接把矩阵与任意向量的乘积 Ab 写成 a×b ,即 Ab=a×b 。
SO(3):3维旋转矩阵
- SO(3):三维旋转群,其元素为旋转矩阵
- 每对旋转矩阵求一次导数,只需左乘一个 反对称矩阵 即可
- 由于 反对称矩阵 反映了R的导数性质,故称它在SO(3)的正切空间(tangent space)上
so(3):3维旋转向量或3维反对称矩阵
- so(3):是一个由三维向量(即 旋转向量 )组成的集合,每个向量对应到一个反对称矩阵,可以表达旋转矩阵的导数
- 反映了R的导数性质
- 旋转轴:旋转向量的方向为旋转轴
- 旋转弧度:旋转向量的长度为旋转的弧度
- 描述了李群 SO(3) 中元素的局部性质
- [a,b]=AB−BA (A、B分别为向量a、b 对应的反对称矩阵)
- [A,B]=−[B,A]
- aaT=AA+||a||2I3×3
指数映射(so(3)⇒SO(3))(罗德里格斯公式)
R(t)=etA=e[V]×,A和[V]×都为反对称矩阵
1)设r为旋转向量,则旋转角度(弧度):θ=||r||
2)把r转换为单位向量:r=1θr
3)e[V]×=eθ[r]×=I+θ[r]×+12!θ2[r]2×+⋅⋅⋅+1n!θn[r]n×=rrT+(θ−13!θ3+15!θ5+⋅⋅⋅)[r]×−(1−12!θ2+14!θ4−⋅⋅⋅)[r]2×=[r]2×+I+sin(θ)[r]×−cos(θ)[r]2×=(1−cos(θ))[r]2×+I+sin(θ)[r]×=cos(θ)I+(1−cos(θ))rrT+sin(θ)[r]×4) 又根据罗德里格斯(Rodrigues)公式: R=cos(θ)I+(1−cos(θ))rrT+sin(θ)[r]×
(5)所以结论为:
R=eθ[r]×=e[V]×每个SO(3)中的元素,都可以找到so(3)一个或多个元素与之对应
so(3)与SO(3)的关系
- 三维旋转表示: 除了采用旋转矩阵描述外,还可以用旋转向量来描述
- 旋转向量的长度(模)表示绕轴逆时针旋转的角度(弧度)
-
旋转向量⇒旋转矩阵
:可以通过
罗德里格斯(Rodrigues)(指数映射)
变换进行转换
1)设r为旋转向量,则旋转角度(弧度):θ=||r||2)把r转换为单位向量:r=1θr3)则旋转矩阵R为:R=cos(θ)I+(1−cos(θ))rrT+sin(θ)[r]×4)OpenCV实现函数:intcvRodrigues2(constCvMat∗src,CvMat∗dst,CvMat∗jacobian=0); 旋转矩阵⇒旋转向量 :
1)弧度:
θ=arccos(tr(R)−12)
2)旋转轴:
Rn=n
3)旋转向量:
v=θn旋转向量可以视为旋转矩阵的导数,指导如何在旋转矩阵中进行微积分运算
- 旋转矩阵:9个自由度,有正交性和行列式值为+1的约束
- 旋转向量:3个自由度,没有约束
- 旋转向量与旋转矩阵:只是表达方式的不同,但表达的东西可以是同一个
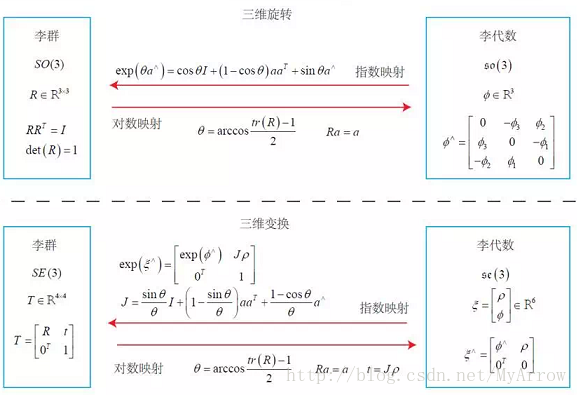
-
指数映射+对数映射关系图
6. 雅可比矩阵与海森矩阵
6.1 雅可比矩阵(Jacobian Matrix)
Reduced Jacobian matrix :降阶雅可比矩阵
雅可比矩阵 :即一阶导数矩阵( 向量对向量的一阶微分矩阵 )
重要性 :它体现了一个可微方程在给定点的最优线性逼近。因此,雅可比矩阵类似于多元函数的导数。
应用领域 :用于向量微积分
雅可比矩阵 :是函数的一阶偏导数以一定方式排列成的矩阵
雅可比矩阵相关的(函数与变量) :多个函数(m个)+多个变量(n个) (映射:Rn→Rm)
定义 :假设某函数从 Rn 映射到 Rm , 其雅可比矩阵是从 Rn 到 Rm 的线性映射,其重要意义在于它表现了一个多变量 向量函数 的最佳线性逼近。因此,雅可比矩阵 类似于单变量函数的导数 。
举例:假设 F:Rn→Rm 是一个从 n 维欧氏空间映射到到
m 维欧氏空间的函数。这个函数由 m 个实函数组成:y1(x1,...,xn),...,ym(x1,...,xn) 。这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵( m×n ),这就是所谓的雅可比矩阵:
⎡⎣⎢⎢⎢⎢⎢⎢⎢∂y1∂x1⋮∂ym∂x1⋯⋱⋯∂y1∂xn⋮∂ym∂xn⎤⎦⎥⎥⎥⎥⎥⎥⎥符号表示 :
JF(x1,⋯,xn),或者∂(y1,⋯,ym∂(x1,⋯,xn
1)F:为其映射的向量函数
2)(x1,⋯,xn):为多变量
3)JF(x1,⋯,xn) :是一个线性映射(矩阵的本质就是线性变换),表示向量函数F在P点 (x1,⋯,xn) 处的Jacobian矩阵(一阶导数矩阵)用途 :
- 如果
p
是
Rn 中的一点, F 在p 点可微分,根据高等微积分, JF(p) 是在这点( p )的导数。 - 在此情况下,
JF(p) 这个线性映射即 F 在点p 附近的最优线性逼近,也就是说当 x 足够靠近点p 时,我们有: - F(x)≈F(p)+JF(p)⋅(x−p)
- 如果
p
是
6.2 海森矩阵(Hessian Matrix)
- 海森矩阵用途:被应用于牛顿法解决的大规模优化问题。
- 海森矩阵变量与函数:一个函数+多个变量 (映射:Rn→R) 。
- 海森矩阵定义:(Hessian matrix 或 Hessian)是一个多变量实值函数的二阶偏导数组成的方块矩阵,假设有一实数函数
f(x1,x2,...,xn)
,如果
f
所有的二阶偏导数都存在,则海林矩阵H为:
- 其
x=(x1,x2,...,xn) - 当函数
f
二阶连续可导时,Hessian矩阵H在临界点
x0 上是一个 n×n 阶的对称矩阵。
- 当H是正定矩阵时,临界点 x0 是一个局部的极小值。
- 当H是负定矩阵时,临界点 x0 是一个局部的极大值。
- H=0,需要更高阶的导数来帮助判断。
- 在其余情况下,临界点 x0 不是局部极值。
6.3 雅可比矩阵与海森矩阵的比较
矩阵属性 雅可比矩阵 (Jacobian Matrix) 海森矩阵 (Hessian Matrix) 用途 1)关节型机器人:关节空间微小运动 dθ 与手部作业空间微小位移dY的关系
2)非线性最小二乘yy 方程 函数向量F由m个实值函数组成:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪y1=f1(x1,⋯,xn)y2=f2(x1,⋯,xn)⋯ym=fm(x1,⋯,xn)也可记为: Y=F(X)
Y=(y1,⋯,ym)T
F=(f2,⋯,fm)T
X=(x1,⋯,xn)T只有一个实值函数组成:
y=f(x1,⋯,xn)
X=(x1,⋯,xn)实值函数个数 m (即m个n元素函数 ) 1 (即1个n元函数) 微分方程组 ⎡⎣⎢⎢dy1⋮dym⎤⎦⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢⎢∂f1∂x1⋮∂fm∂x1⋯⋱⋯∂f1∂xn⋮∂fm∂xn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎡⎣⎢⎢dx1⋮dxn⎤⎦⎥⎥
即:dY=JF(X)dX方程组是一个关于微分的线性方程组,其系数矩阵即雅可比矩阵定义 JF(X)=⎡⎣⎢⎢⎢⎢⎢⎢⎢∂f1∂x1⋮∂fm∂x1⋯⋱⋯∂f1∂xn⋮∂fm∂xn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢∂2f∂x1∂x1∂2f∂x2∂x1⋮∂2f∂xn∂x1∂2f∂x1∂x2∂2f∂x2∂x2⋮∂2f∂xn∂x2⋯⋯⋱⋯∂2f∂x1∂xn∂2f∂x2∂xn⋮∂2f∂xn∂xn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥导数阶数 一阶偏导数 二阶偏导数 矩阵类型 m×n (一般不为方阵) n×n (方阵) 映射 Rn→RmJ为Y随X变化而变化的线性变换
- 灰色的为坐标系1 (
V1=(322)T
),黑色的为坐标系2 (
V2=(112)T








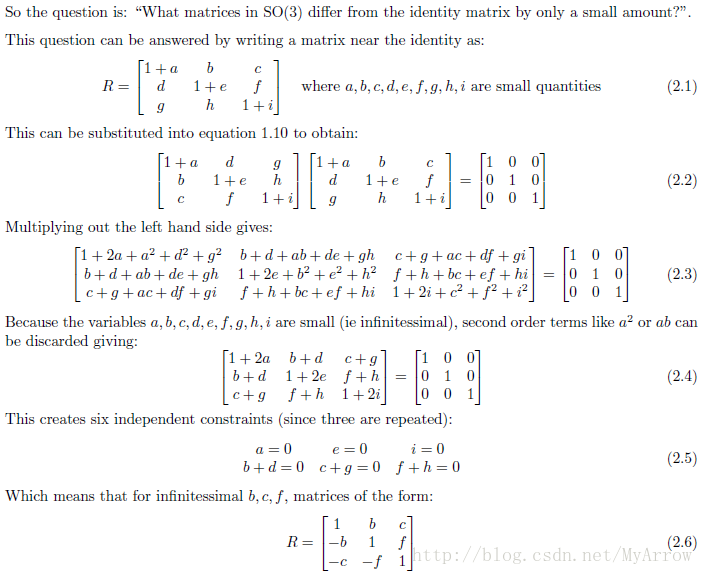

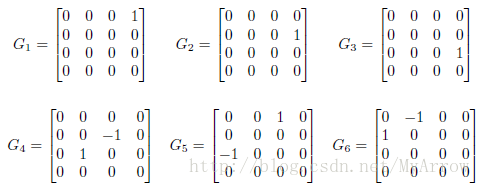














 7373
7373











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








