Fibonacci数列

中学的数学规律题目中常常见到这样的一组数：1,1,2,3,5,8,13,21,34,55,89,144,233...。这组数在数学上，常被人们称作Fibonacci数列。

1202年，意大利数学家斐波那契出版了他的《算盘全书》。他在书中提出了一个关于兔子繁殖的问题：如果一对兔子每月能生一对小兔（一雄一雌），而每对小兔在它出生后的第三个月里，又能开始生一对小兔，假定在不发生死亡的情况下，由一对出生的小兔开始，50个月后会有多少对兔子？

在第一个月时，只有一对小兔子，过了一个月，那对兔子成熟了，在第三个月时便生下一对小兔子，这时有两对兔子。再过多一个月，成熟的兔子再生一对小兔子，而另一对小兔子长大，有三对小兔子。如此推算下去，我们便发现一个规律：

时间（月）	初生兔子（对）	成熟兔子（对）	兔子总数（对）
1	1	0	1
2	0	1	1
3	1	1	2
4	1	2	3
5	2	3	5
6	3	5	8
7	5	8	13
8	8	13	21
9	13	21	34
10	21	34	55

 

 

 

 

 

 

 

由此可知，从第一个月开始以后每个月的兔子总数是：1,1,2,3,5,8,13,21,34,55,89,144,233...。若把上述数列继续写下去，得到的数列便称为斐波那契数列。数列中每个数便是前两个数之和，而数列的最初两个数都是1。

若设F₀=1, F₁=1, F₂=2, F₃=3, F₄=5, F₅=8, F₆=13...，则：当n＞1时，F_n+2 = F_n+1 + F_n，而F₀=F₁=1。
下面是一个古怪的式子：

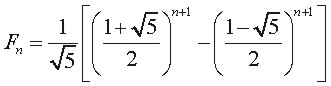
F_n看似是无理数，但当n ≧0时，F_n都是整数

利用斐波那契数列来做出一个新的数列：方法是把数列中相邻的数字相除，以组成新的数列如下：

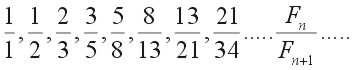
当n无限大时，数列的极限是：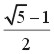

这个数值称为黄金分割比，它正好是方程式x²+x-1=0的一个根。

C++程序：

//Program to generate the first 15 Fibonacci numbers
#include<stdio.h>
int main (void)
{
    int Fibonacci[15],i;
    Fibonacci[0]=1;
    Fibonacci[1]=1;
    for(i=2;i<15;++i)
       Fibonacci[i]=Fibonacci[i-2]+Fibonacci[i-1];
    for(i=0;i<15;++i)
        printf("%i/n",Fibonacci[i]);
    return 0;
}

Fibonacci数列在很多领域都有体现，不仅是兔子的繁殖上，在一般经济的发展上，在股票等资本市场的预测上也很有用。

后记：对Fibonacci数列产生兴趣是从《越狱》开始的，片中有个人物叫Fibonacci，一开始觉得很好听，一定是个意大利人的名字，后来才知道是个数学家的名字。这会儿刚刚看了《达芬奇密码》，里面也说到Fibonacci数列，这就把这篇文章收录到自己的博客中来，因为数学也是我最近研究的课题。