回溯法---->8-皇后问题

八皇后问题

问题描述

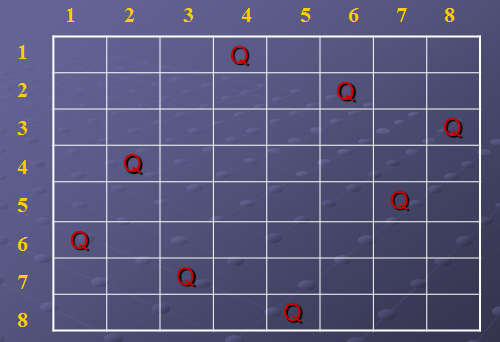
将n个皇后放置在一个n×n的棋盘上，要求使得每两个之间都不能互相“攻击”，也就是使得每两个都不能在同一行、同一列及同一条斜角线上。

分析

• 8皇后问题的解可以表示为8-元组(x₁,…,x₈) ，其中其中x_i是第i行皇后所在的列号。
• 显式约束条件是s_i={1,2,3,4,5,6,7,8}, 1≤i≤8
• 隐式约束条件是，没有两个x_i可以相同且没有两个皇后可以在同一条斜角线上。
• 解空间的大小8!个

测试两个皇后在一条斜角线的方法

假设有两个皇后被放置在(i, j)和(k,l)位置上，那么根据以上所述，仅当i – j = k - l 或 i + j = k + l时，它们才在同一条斜角线上。将这两个等式分别变换成j – l= i - k　和 j – l = k - i　 因此，当且仅当| j – l | = | i – k |时。两个皇后在同一条斜角线上。

检测放置新皇后的算法

过程PLACE(k)测试两种情况，即X(k)是否不同于前面X(1),…,X(k-1)的值以及在同一个斜角线上是否根本就没有别的皇后。

procedure PLACE(k) //如果一个皇后可以放在第k行和X(k)列，则返回true；否则返回false//     global X(1:k); integer i ,k     i ← 1 　 while i<k do        if X(i)=X(k)//在同一列有两个皇后            or ABS(X(i)-X(k))=ABS(i-k)//在同一条斜角线上              then return (false)              i ← i + 1       repeat       return (true) End PLACE

8-皇后问题求解算法

过程NQUEENS求n-皇后问题的所有解

procedure NQUEENS(n)    integer k, n, X(1:n)    X(1) ← 0; k ← 1 　　//K是当前行；X(k)是当前列     while k>0 do　　　　　 //对所有的行执行一下语句          X(k) ←X(k)+1           //移到下一列          while X(k) ≤ n and not PLACE(k) do //此处能放这个皇后吗         X(k) ←X(k)+1      repeat      if X(k) ≤ n 　　 //找到一个位置      then if k=n　　　 //是一个完整的解吗           then print (X) //是，打印这个数组           else k ← k+1 , X(k) ← 0　 //转到下一行            endif       else k ← k-1 //回溯      endif    repeat End NQUEENS