15-谜问题
一、问题描述
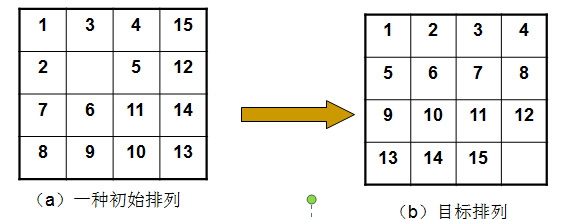
在一个分成16格的方形棋盘上放有15块编了号的牌。对于这些牌给定的一种初始排列,要求通过一系列的合法移动将初始排列转换成目标排列。
合法移动:每次将一个邻接于空格的牌移动到空格位置
(注:并不是所有的初始状态都能变换成目标状态的)
二、如何判定目标状态在初始状态的状态空间中?
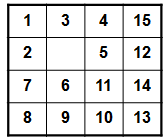
1.记POSITION(i)为编号为i的牌在初始状态中的位置;POSITION(16)表示空格的位置。
POSITION(1:16)=(1,5,2,3,7,10,9,13,14,15,11,8,16,12,4,6)
2.记LESS(i)是这样牌j的数目:j<i,但POSITION(j)> POSITION(i),即编号小于i但初始位置在i之后的牌的数目。
例:LESS(1)=0; LESS(4)=1; LESS(12)=6
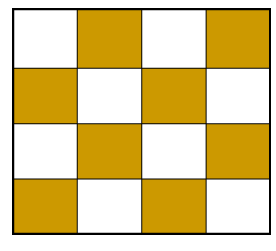
3.引入一个量X
如图所示,初始状态时,若空格落在橙色方格上,则X=1:若空格落在白色方格上,则X=0。
4.目标状态是否在初始状态的状态空间中的判别条件:
当且仅当 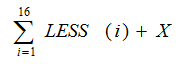
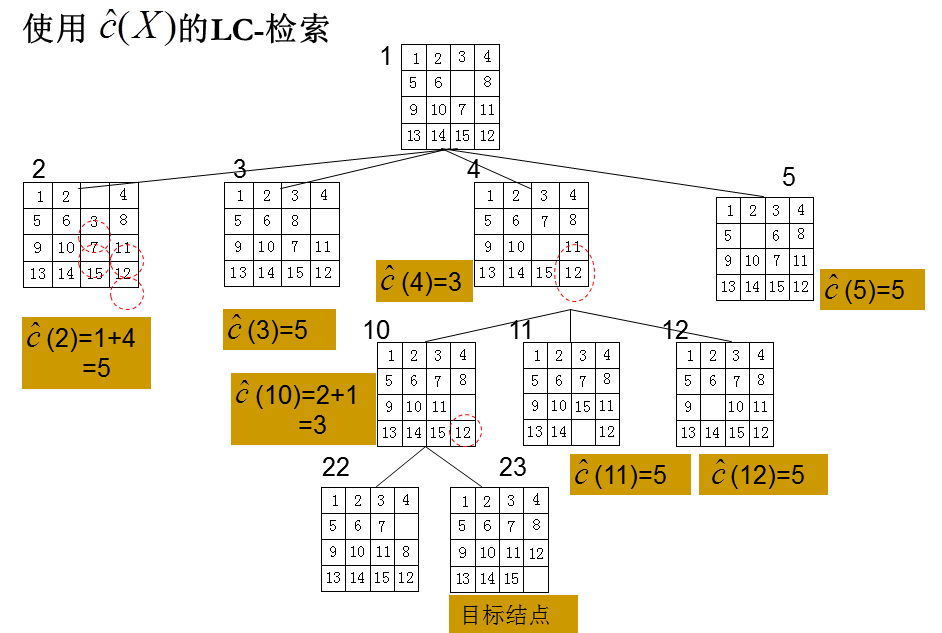
三、成本估计函数
(X)是由根到结点X的路径长度
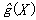
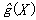
四、例子








 本文探讨了15-谜问题的基本概念与解决方法。详细介绍了如何通过合法移动将初始排列转换为目标排列,并给出了判断目标状态可达性的条件及成本估计函数。
本文探讨了15-谜问题的基本概念与解决方法。详细介绍了如何通过合法移动将初始排列转换为目标排列,并给出了判断目标状态可达性的条件及成本估计函数。

















 892
892

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








