莫比乌斯反演是数论中很重要的内容,可以优雅解决很多数论的问题。之前浅学了一下,这两天寒假专题训练又拾起来刷了些题,想总结一下。由于内容较多本文证明部分会跳过一些,更着重于莫比乌斯反演在解题中的实际应用。
预备知识:
首先介绍一下什么是莫比乌斯函数:
B - GCD
Time Limit:3000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u
Submit
Description
Please notice that, (x=5, y=7) and (x=7, y=5) are considered to be the same.
Yoiu can assume that a = c = 1 in all test cases.
Input
Each case contains five integers: a, b, c, d, k, 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000, as described above.
Output
Sample Input
2
1 3 1 5 1
1 11014 1 14409 9
Sample Output
Case 1: 9
Case 2: 736427
Hint
For the first sample input, all the 9 pairs of numbers are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 5), (3, 4), (3, 5).
在问题中我们需要求的是1<=x<=n,1<=y<=m中gcd(x,y)==k的组数,也就是
其中[x]表示sigma(x)。显然这里是可以用容斥搞的,但之后我们会发现莫比乌斯反演法的话更加好写,也快得多
那么这个地方怎么用莫比乌斯反演法呢
我们让f(n,m,k)表示1<=x<=n,1<=y<=m中gcd(x,y)==k的组数,也就是(*)式
再让F(n,m,k)表示1<=x<=n,1<=y<=m中gcd(x,y)是k的倍数的组数
F(n,m,k)很好求,显然F(n,m,k) =
而题目的目标是求f(n,m,k)
那么很显然,满足莫比乌斯反演的第二种形式
根据莫比乌斯反演法,我们得到
由于F(d)我们是知道的,所以有了这个式子f(k)就可以求出来了,只要枚举每个k的倍数作为d然后求和就可以了
到这里这道题已经可做了。
但这样还不够好:复杂度无法降低,莫比乌斯反演法很多题目对f(k)运算速度要求sqrt(n)甚至是更低,而现在这个的复杂度是min(n,m)/k。
不过幸好我们稍微转换一下思考方式就能得到一个形式更简单的算法:
考虑下面这句话:1<=x<=n 1<=y<=m中 gcd(x,y)==k 的对数相当于 1<=x<=n/k 1<=y<=m/k 中gcd(x,y) == 1的对数。
这句话是很显然的,因为gcd(x,y)==k每一对的x和y除k之后必然映射到一组1<=x<=n/k1<=y<=m/k中一组gcd(x,y) == 1的x和y,反之亦然。
这样的话,我们就可以把从gcd(x,y)==k的问题全部转换成在求gcd(x,y)==1的问题,只是上下界变动一下而已。
我们带入k=1,
我们知道f(1)表示的是gcd(x,y)==1,也就是x,y互质的对数。
结合上面的分析不难发现
那么我们就把f(k)的求解转换成了一端连续值的求和了,从编程角度比之前简单了许多。
到这一步对于解决上面一道题来说是游刃有余了。
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
#define FILL(x) memset((x),0,sizeof(x))
const int maxn = 100000+20;
bool check[maxn];
int mu[maxn];
int prime[maxn];
void Mobius(int N)
{
FILL(check);
mu[1] = 1;
int tot = 0;
for(int i=2;i<=N;i++){
if(!check[i]){
prime[tot ++] = i;
mu[i] = -1;
}
for(int j=0;j<tot;j++){
if(i * prime[j] > N)break;
check[i * prime[j]] = true;
if(i % prime[j] == 0){
mu[i * prime[j]] = 0;
break;
}else{
mu[i * prime[j]] = -mu[i];
}
}
}
}
int a,b,c,d,k;
int cases;
ll ans;
void solve()
{
ans = 0;
if(k == 0){
printf("Case %d: 0\n",cases);
return ;
}
b/=k;d/=k;
if(b>d)swap(b,d);
for(int i=1;i<=b;i++){
ans += (ll)mu[i] * (b/i) * (d/i);
}
ll ans2 = 0;
for(int i=1;i<=b;i++){
ans2 += (ll)mu[i] * (b/i) * (b/i);
}
ans -= ans2/2;
printf("Case %d: %I64d\n",cases,ans);
}
int main()
{
Mobius(100001);
int T;
scanf("%d",&T);
cases = 0;
while(T--){
cases ++;
scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
solve();
}
return 0;
}但是正如之前所说有些题目对f(k)的求解速度要求比较严格,比如下面这道题:
G -Problem b
Description
Input
第一行一个整数n,接下来n行每行五个整数,分别表示a、b、c、d、k
Output
共n行,每行一个整数表示满足要求的数对(x,y)的个数
Sample Input
2 2 5 1 5 1 1 5 1 5 2
Sample Output
14 3
Hint
100%的数据满足:1≤n≤50000,1≤a≤b≤50000,1≤c≤d≤50000,1≤k≤50000
这道题数据量很大,每组数据O(n)处理的话是不够的,我们需要分块加速,这也是转换成求f(1)的最大好处之一。
转换成gcd(x,y)==1之后我们发现d的取值是连续的,而n/d和m/d在d在一定范围的时候是不会变化的,我们称这样的区间叫不变块。我们可以把每一个不变块中的mu[i]求和之后乘上n/d和m/d加到答案里。
每个不变块中的求和工作只要预处理一下mu[i]的前缀和就能轻松搞定,这样的话我们求和时就可以每次求一块的和,而不是一个个求和了,速度大大加快,达到sqrt(n)。
而d属于[x,n/(n/x)]这个区间中时n/d的值是不变的,对m也是一样。那么假设当前块的初始点为x,这个块的末尾点就是min(n/(n/x),m/(m/x))(因为n/d和m/d都要保持不变)。然后就可以一块一块求和了。
说上去也许稍微有点复杂,但看一下代码应该就很容易理解了
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
#define FILL(x) memset((x),0,sizeof(x))
const int maxn = 100000+20;
bool check[maxn];
int mu[maxn];
int prime[maxn];
int sum[maxn];
void Mobius(int N)
{
FILL(check);
mu[1] = 1;
int tot = 0;
for(int i=2;i<=N;i++){
if(!check[i]){
prime[tot ++] = i;
mu[i] = -1;
}
for(int j=0;j<tot;j++){
if(i * prime[j] > N)break;
check[i * prime[j]] = true;
if(i % prime[j] == 0){
mu[i * prime[j]] = 0;
break;
}else{
mu[i * prime[j]] = -mu[i];
}
}
}
}
int a,b,c,d,k;
int cases;
ll calc(int b,int d)
{
ll ans = 0;
b/=k;d/=k;
if(b>d)swap(b,d);
for(int i=1,last=i;i<=b;i=last+1){//i是不变块的左边界
last = min(b/(b/i),d/(d/i));//last是不变块的右边界
ans += (ll)(sum[last]-sum[i-1]) * (b/i) * (d/i);
}
return ans;
}
void solve()
{
if(k == 0){
printf("0\n");
return ;
}
ll ans1 = calc(b,d);
ll ans2 = calc(a-1,d);
ll ans3 = calc(b,c-1);
ll ans4 = calc(a-1,c-1);
ll ans = ans1 - ans2 - ans3 + ans4;
printf("%lld\n",ans);
}
int main()
{
Mobius(100001);
sum[0] = 0;
for(int i=1;i<maxn;i++)sum[i]=sum[i-1]+mu[i];
int T;
scanf("%d",&T);
cases = 0;
while(T--){
cases ++;
scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
solve();
}
return 0;
}到这里应该能基本解决求GCD(x,y)==k的组数这类问题,也是莫比乌斯反演法最基本的应用了。更高级的用法实际上都是从这个基础出发的。更多用到的是莫比乌斯反演最初始的定义式构造函数进行推导了。
再次强烈推荐jzp大神的ppt点击打开链接,做莫比乌斯反演首先要会线性筛求出莫比乌斯函数。从他的ppt中可以看到另外一种应用方法,紧紧围绕下面两个重要公式(上下分别为莫比乌斯函数和欧拉函数):
有了这两个式子在做题时很多时候可以省去构造函数的过程,直接套用,在ppt中的应用也非常精彩,推荐推荐。
内容比较初步,后面可能带来剩下几题题解,大家请随意吐槽指教。





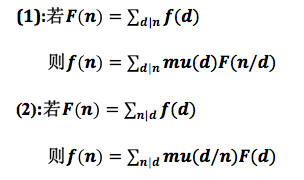
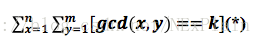
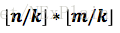
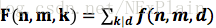
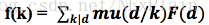
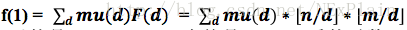
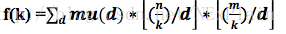
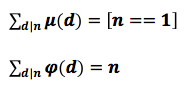
















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








