为什么使用卷积层替代CNN末尾的全连接层

最新推荐文章于 2025-06-11 21:14:44 发布
最新推荐文章于 2025-06-11 21:14:44 发布
阅读量2.3w 收藏 25
点赞数 2
CC 4.0 BY-SA版权
分类专栏： 机器学习 深度学习之为什么系列
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/nnnnnnnnnnnny/article/details/70194432
本文介绍了全卷积神经网络(FCN)的概念及其优势。详细解释了通过将传统CNN中的全连接层替换为卷积层，使网络能够处理任意大小的输入图像，并应用于语义分割等任务。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

CNN网络的经典结构是： 输入层—>（卷积层+—>池化层？）+—>全连接层+
（其中+表示至少匹配1次，？表示匹配0次或1次）

全卷积神经网络Fully Convolutional Network (FCN)

全卷积神经网络即把CNN网络最后的全连接层替换为卷积层。为什么这么做？换句话说这样会带来什么好处呢？

  1. 首先，说一下卷积层和全连接层的区别：卷积层为局部连接；而全连接层则使用图像的全局信息。可以想象一下，最大的局部是不是就等于全局了？这首先说明全连接层使用卷积层来替代的可行性。

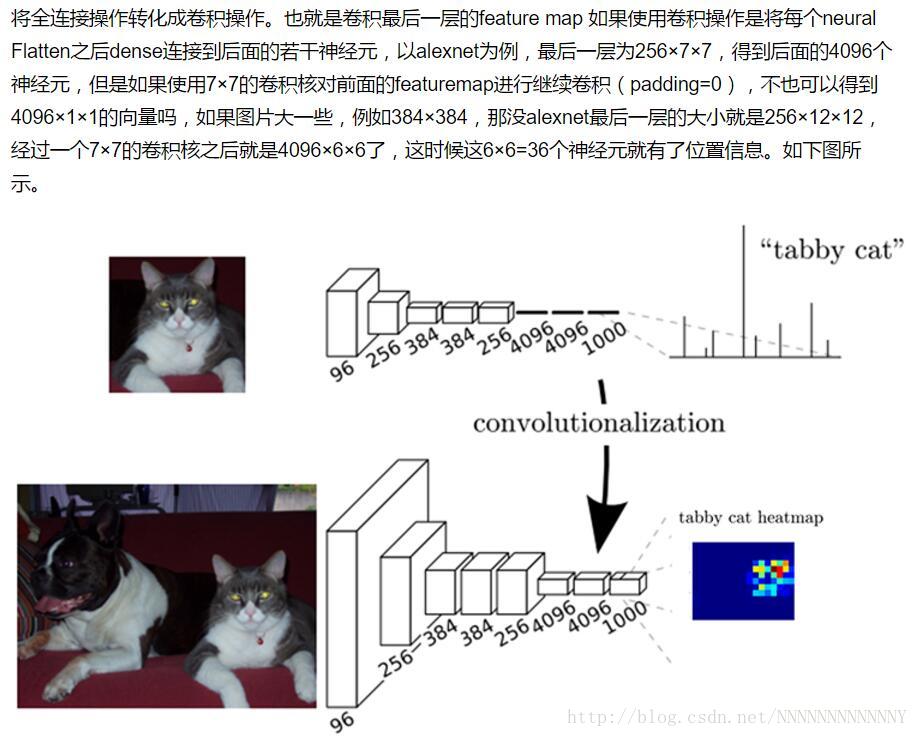
  2. 然后，究竟使用卷积层代替全连接层会带来什么好处呢？答案：可以让卷积网络在一张更大的输入图片上滑动，得到每个区域的输出（这样就突破了输入尺寸的限制）。论文里Fully Convolutional Networks for Semantic Segmentation介绍的很清楚，解读如下：
    这里写图片描述
    需要说明的是这一特性不仅可用于语义分割，在物体分类、目标检测中都可以使用。

参考：
How does the conversion of last layers of CNN from fully connected to fully convolutional allow it to process images of different size?
CS231n课程笔记翻译：卷积神经网络笔记
论文笔记–Fully Convolutional Networks for Semantic Segmentation

【图像去噪】论文精读：Multi-level Wavelet-CNN for Image Restoration（MWCNN）
主要更新底层视觉（去噪、超分等）相关的科研内容，形式为【论文精读】+【论文复现】
08-27 1782
论文题目：Multi-level Wavelet-CNN for Image Restoration —— 用于图像恢复的多级小波CNNCVPR 2018！感受野大小和效率之间的权衡是低级视觉中的关键问题。普通卷积网络 (CNN) 通常以计算成本为代价来扩大感受野。最近，已经采用扩张过滤来解决这个问题。但它受到网格效应的影响，由此产生的感受野只是具有棋盘图案的输入图像的稀疏采样。在本文中，我们提出了一种新颖的多级小波 CNN (MWCNN) 模型，以更好地权衡感受野大小和计算效率。
故障诊断 | CNN-GRU-Attention故障诊断
最新发布
机器学习之心的博客，关注并私信文章链接，获取对应文章源码和数据。
07-05 144
故障诊断 | CNN-GRU-Attention故障诊断
cnn输入层_CNN中使用卷积层替代全连接层训练
weixin_39527768的博客
11-20 291
在吴恩达的深度学习的卷积神经网络课程中，对于目标识别介绍了一种划窗方法，在该方法的实现中使用卷积层替代最后的全连接(FC)层例如，在常规的CNN中，最后的部分是FC层，由于其参数与输入数据的大小（H和W）有关，所以训练好了之后就只能预测28x28的规模的图片，如下图这样：28x28但是有时候碰到其他规模的图片的话就没办法了，比如下面的这张：60x60我希望网络能够根据这张图片给出一组预测。如果是常...
卷积层(FCN)替换全连接层(FC)的意义
帅的发光发亮的博客
05-07 2万+
1.卷积层替换全连接层的可行性： 卷积层是局部连接，它的特点是稀疏连接和权值共享；而全连接层使用了图像的全局信息，每个神经元都与上一层的所有神经元相连接。 “最大的局部”和“全局”这两个概念其实是等价的，因此卷积层替换全连接层是可行的。 2.全连接层到卷积层的转换： 下图显示了AlexNet卷积化的过程，假设执行特征提取的卷积层的最后一层输出为256×7×7，得到后面的4096个神经元；那么改为用7×7的卷积核对该256×7×7的输出特征图做卷积，也可以获得4096×1×1的向量。由于卷积核大小和输入的特征
全连接层和卷积层
Humbunklung的专栏
06-11 1165
卷积层的参数和计算方式与全连接层完全一致，能够实现相同的线性变换。因此，在实际应用中，可以通过调整卷积核的大小和参数设置，使卷积层严格等价于全连接层。 卷积层不仅能实现全连接层的功能，还能更高效地处理具有空间结构的数据，是深度学习中图像等任务的首选结构。
神经网络改进方案：全局平均池化替代全连接层
weixin_44438120的博客
11-18 1万+
基本原理 全局平均池化英文名为：global average pooling简称为GAP 其具体实现过程在原文 << Network In Network >> 中为： 可以看出其是将矩阵中的 [w,h] ,进行平均池化变为一个单元。也即进行Flattrn和FC。其详细原理的图形示例可参考下图： 其实也就是通过池化层将原有的输入为 [b,c,h,w] 减少成 [b,c,1,1] 的尺寸也即上文提到的将 [w,h] 进行平均池化变为一个单元。 与FC层区别 在常见的卷积神经网络中
为什么我们更多的使用卷积神经网络而不用全链接神经网络
weixin_38241876的博客
06-07 1489
首先全连接有一个问题就是参数量特别大，参数量一多就会占用内存，而且随着网络层数的增加会指数级的增长。 第二一点就是由于全连接将所有信息量都考虑到了，并且不分重要和不重要，会将一些噪声也学习到，容易造成过拟合，需要使用dropout来防止过拟合。 卷积的好处就是不会考虑全部信息，不会想全连接那样所有特征，不管是重要还是不重要的都一视同仁，它就像人在看东西一样会有所侧重，学到关键的特征。 在卷积...
【模型复现】Network in Network，将1*1卷积引入网络设计，运用全局平均池化替代全连接层。模块化设计网络
白水空空
04-07 851
全连接层参数量是非常庞大的，模型通常会容易过拟合，针对这个问题，Hinton提出Dropout方法来提高泛化能力，但是全连接的计算量依旧很大。基于此，论文提出。
Faster R-CNN和SSD 重点内容（内附卷积层与全连接层区别）
q199502092010的博客
12-26 6460
首先需要说明的是，本文在写时仅仅依靠着对论文的解读，具体代码的实现还没有看。最终可能也不一定会看源码，会找一个合适的进行详细的学习。通过阅读以下两篇论文及翻译，总结出一些网络的特点记录在这里，方便之后的查找。 Faster R-CNN https://arxiv.org/abs/1506.01497 翻译：https://blog.csdn.net/quincuntial/article/det...
cnn输入层_一个小改动，CNN输入固定尺寸图像改为任意尺寸图像
weixin_39888049的博客
11-20 1018
点击上方“小白学视觉”，选择“星标”公众号重磅干货，第一时间送达本文小白将和大家一起学习如何在不使用计算量很大的滑动窗口的情况下对任意尺寸的图像进行图像分类。通过修改，将ResNet-18CNN框架需要224×224尺寸的图像输入改为任意尺寸的图像输入。首先，我们澄清一个对卷积神经网络(CNN)的误解。卷积神经网络不需要固定大小的输入如果用过CNN对图像进行分类，我们需要对输入图像进行裁...
深度学习面试笔试之卷积神经网络(CNN)
算法工程师
10-21 1120
深度学习面试笔试之卷积神经网络(CNN)
卷积层代替全连接层
时光机 °的博客
08-01 1万+
为什么卷积层可以“代替”全连接层？   卷积和全连接的区别大致在于：卷积是局部连接，计算局部信息；全连接是全局连接，计算全局信息。（但二者都是采用的点积运算）   但如果卷积核的kernel_size和输入feature maps的size一样，那么相当于该卷积核计算了全部feature maps的信息，则相当于是一个kernel_size∗1kernel_size∗1kernel\_size...
全连接层的作用_CNN中使用卷积代替全连接
weixin_39847945的博客
11-30 1300
船长黑板报所有文章和代码的最新版本均在Captain1986/CaptainBlackboard​github.com维护，知乎不做维护您的Star是对我的鼓励## 引言在经典分类网络，比如LeNet、AlexNet中，在前面的卷积层提取特征之后都串联全连接层来做分类。但是近些年来，越来越多的网络，比如SSD，FasterRCNN的RPN，MTCNN中的PNet，都使用卷积层来代替全连接，也一样可...
卷积神经网络在分类层用卷积层代替全连接层的好处（附代码演示）
Amigo_1997的博客
02-25 6502
先说一下结论： 好处：可以让同一个训练batch中的图像大小的不一样，全连接层则必须输入图像的大小固定。 分析过程： 全连接层—代码演示具体操作 假设batch-size是1，最后的卷积层输出大小是5X5，通道数是512的话，如果接全连接层的话，就需要先reshape成一维的，这里的dim=12800（5X5X512），这里全连接层的权重矩阵大小就固定为了[12800,256]（全连接...
卷积神经网络全连接层详解：特征汇总、FCN替代与性能影响分析
2501_90186640的博客
05-14 1183
本文聚焦CNN的全连接层，详细介绍其将二维特征图转化为一维向量的过程，阐述全卷积网络（FCN）如何通过转置卷积替代全连接层以实现像素级分类，并分析全连接层对图像分类任务中CNN性能的具体影响
CNN中全连接层是什么样的？
热门推荐
有信念，才能走的更远
09-22 3万+
名称：全连接。意思就是输出层的神经元和输入层的每个神经元都连接。 例子： AlexNet  网络中第一个全连接层是这样的： layer {   name: "fc6"   type: "InnerProduct"   bottom: "pool5"   top:"fc6"   param {     lr_mult: 1     decay_mult: 1   }   par
cnn输入层_CNN多尺度特征提取
weixin_39945523的博客
10-21 1295
众所周知通常CNN要求输入图像尺寸是固定的，比如现有的效果比较好的pre-trained的模型要求输入为224*224，227*227等。这个要求是CNN本身结构决定的，因为CNN一般包括多个全连接层，而全连接层神经元数目通常是固定的，如4096，4096，1000。这一限制决定了利用CNN提取的特征是单一尺度的，因为输入图像是单一的。 多尺度特征（multi-scale feat...
MYSQL自然连接
xiaokkya的博客
12-03 2481
自然连接 目标：了解自然连接的特性，知道自然连接的使用方式。 概念：natural join,是一种自动寻找连接条件的连接查询。 重点： 1.自然连接包含自然内连接和自然外连接。 自然内连接： natural join 自然外连接： natural left/right join 2.自然连接条件匹配模式：自动寻找相同字段名作为连接条件（字段名相同）。 步骤： 1.需要进行连表查询结果。 2.连表查询的表字段能够直接关联（字段名字相同：非常高的表结构设计） 3.选择合适的连接方式：内连接o
深度学习基础：1x1的卷积为什么代替全连接
weixin_43507744的博客
05-18 4399
1x1的卷积作用我们肯定很好理解： 跨通道的特征整合 比如：输入的特征是32x64x64（32为通道数），我想要把32个通道的信息进行融合，最后输出8个特征，那我们就可以设计1x1的卷积核为：输入通道：32，输出通道：8。 特征通道的升维和降维 上面的例子也是一个降维的操作，我们把32通道的特征图融合成了8通道的特征图，这样做可以融合不同的特征模式（其本质是增大感受野）。 升维是把特征上升到更高维度，比如，我们设计1x1卷积核为：输入通道：32，输出通道：64，这样可以得到更多的特征模式。 减少卷积
之前提到的全连接网络是什么？
03-28
<think>好的，我现在需要回答用户关于全连接网络的问题。用户之前问过图像分割为什么输出是图片，现在接着问全连接网络是什么。首先，我得回想一下之前在图像分割的回答中提到的全连接网络（FCN），即全卷积网络，可能用户在这里有混淆，因为全连接网络（Fully Connected Network）和全卷积网络（Fully Convolutional Network）缩写都是FCN，但其实是不同的概念。我需要确认用户指的是哪一个。 根据之前的对话，在图像分割部分提到的是全卷积网络（Fully Convolutional Network），用于保持空间分辨率。但用户现在问的是“全连接网络”，这可能指的是传统的全连接神经网络，即多层感知机（MLP），或者可能混淆了全卷积网络。这时候需要先明确术语，但可能用户确实想了解传统的全连接网络，即Fully Connected Network，所以需要分情况说明。 首先，我应该解释全连接网络的基本结构，即每一层的每个神经元都与下一层的所有神经元连接，没有保留空间信息，适用于分类任务。然后对比之前在图像分割中提到的全卷积网络（FCN），说明两者的区别，避免混淆。同时要联系用户之前的提问，解释为什么在图像分割中使用全卷积而不是全连接网络，因为全连接会丢失空间信息，导致无法进行像素级预测。 接下来需要结构清晰，分点解释全连接网络的结构、应用场景、局限性，以及与全卷积网络的区别。可能还需要提到全连接层在卷积神经网络中的位置，比如在CNN末尾用于分类。同时要举例说明，比如图像分类中的全连接层将特征图展平后输出类别概率。 需要确保使用中文，术语准确，比如“全连接层”、“卷积层”、“空间维度”等。同时注意使用LaTeX格式表达公式，比如全连接层的计算可以用矩阵乘法表示，例如$y = Wx + b$。还要检查是否符合之前的系统级指令，如行内公式用$...$，独立公式用$$...$$，结构清晰，分步骤说明。 可能用户有误解，所以需要明确全连接网络和全卷积网络的不同，尤其是在处理图像数据时的差异。需要强调全连接网络在处理图像时的缺点，比如参数过多，丢失空间信息，而全卷积网络通过保持空间结构更适合分割任务。 最后总结全连接网络的定义、结构、应用及与全卷积网络的对比，确保用户能清楚区分两者，并理解为什么图像分割中使用的是全卷积网络而不是全连接网络。</think>### **全连接网络（Fully Connected Network, FCN）详解** --- #### **1. 全连接网络的基本定义** **全连接网络**（又称**多层感知机，MLP**）是一种经典的神经网络结构，其核心特点是**相邻层的所有神经元之间均存在连接**。 - **结构特性**：每个神经元的输入是前一层所有神经元的输出加权和（通过激活函数非线性化）。 - **数学表达**：对于第$l$层的输出$\mathbf{h}^{(l)}$，其计算为： $$ \mathbf{h}^{(l)} = \sigma\left( \mathbf{W}^{(l)} \mathbf{h}^{(l-1)} + \mathbf{b}^{(l)} \right) $$ 其中： - $\mathbf{W}^{(l)}$为权重矩阵，$\mathbf{b}^{(l)}$为偏置向量 - $\sigma$为激活函数（如ReLU、Sigmoid） --- #### **2. 全连接网络的结构与特点** ##### **(1) 典型结构示意图** ``` 输入层 → 隐藏层（全连接） → 隐藏层（全连接） → 输出层 ``` - **输入层**：接收一维向量（例如图像需展平为$H \times W \times 3 \rightarrow D$维向量）。 - **隐藏层**：通过全连接层逐步提取特征。 - **输出层**：根据任务需求输出结果（如分类概率、回归值）。 ##### **(2) 核心特点** | 特性 | 说明 | |---------------------|----------------------------------------------------------------------| | **全局感知** | 每个神经元与前一层的所有神经元连接，能捕捉全局特征。 | | **参数密集** | 参数量为$N_{\text{in}} \times N_{\text{out}}$，易导致过拟合（例如输入$1000$维，隐藏层$500$维 → 参数$50$万）。 | | **空间信息丢失** | 输入需展平为一维向量，破坏图像、语音等数据的空间或时序结构。 | --- #### **3. 全连接网络的应用场景** ##### **(1) 传统分类任务** - **图像分类**：早期LeNet等网络在末尾使用全连接层输出类别概率（需将卷积层输出的特征图展平）。 - **结构化数据预测**：如房价预测、用户评分预测等（输入为表格数据）。 ##### **(2) 与其他网络的结合** - **卷积神经网络（CNN）**：全连接层常作为CNN的末尾分类器（例如ResNet最后一层为全连接层）。 - **循环神经网络（RNN）**：全连接层用于处理时序数据的最终输出（如语言模型预测下一个词）。 --- #### **4. 全连接网络的局限性** ##### **(1) 对图像任务的缺陷** - **输入需展平**：例如将$256 \times 256 \times 3$的图像展平为196,608维向量，导致： - 参数爆炸（假设隐藏层1000维 → 参数量约2亿）。 - 无法保留像素间的空间相关性（如边缘、纹理等局部特征）。 - **效率低下**：大量参数计算耗时长，难以处理高分辨率图像。 ##### **(2) 与全卷积网络（Fully Convolutional Network）的对比** | 特性 | 全连接网络（MLP） | 全卷积网络（FCN） | |---------------------|---------------------------------------|---------------------------------------| | **输入处理** | 展平为一维向量 | 保留原始空间维度（如$H \times W \times C$） | | **参数效率** | 参数量大，易过拟合 | 参数共享，效率高 | | **适用任务** | 分类、回归 | 图像分割、目标检测等需空间信息的任务 | | **典型应用** | MNIST手写数字分类 | U-Net医学图像分割 | --- #### **5. 为什么图像分割不用全连接网络？** 以图像分割任务为例，需输出与输入尺寸相同的像素级标签图，全连接网络的缺陷尤为明显： 1. **空间信息丢失**：展平操作破坏像素位置关系，无法精确定位目标边界。 2. **参数不可行**：假设输入为$256 \times 256$图像，输出同尺寸标签图，则全连接层参数量为： $$ (256 \times 256 \times 3) \times (256 \times 256) \approx 3.87 \times 10^{11} $$ （完全无法训练） 3. **计算效率低**：高分辨率图像会导致计算量剧增。 --- #### **6. 全连接网络的改进与替代方案** ##### **(1) 改进方法** - **参数缩减**：通过降维（PCA、自动编码器）减少输入维度。 - **正则化**：使用Dropout、L2正则化防止过拟合。 ##### **(2) 替代方案** - **卷积神经网络（CNN）**：通过卷积核局部感知、参数共享高效提取空间特征。 - **全卷积网络（FCN）**：用转置卷积替代全连接层，保留空间信息（如图像分割任务）。 --- #### **总结** - **全连接网络**是基础的神经网络结构，适用于全局特征提取和分类任务，但**参数密集且破坏空间信息**。 - 在图像分割等需空间信息的任务中，**全卷积网络（FCN）**通过保留输入输出的空间维度，成为更优选择。 - 理解全连接网络的局限性，有助于合理选择网络结构（例如：图像任务优先使用CNN/FCN，结构化数据可使用MLP）。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值