四则混合运算表达式分析程序的原理及其实现

意义： 四则混合运算表达式可以看作一定语言中的表达式分析及求值，虽然它很小，却是一个语法分析的很好的例子！

一、目标：可以对输入的四则混合运算表达式进行分析，并求出其结果。程序须支持：整数及小数运算、支持加（+），减（-），乘（*），除（/），技术括号嵌套。

二、原理：表达式的分析过程可以看作三步，（1）分析出表达式中各个标记，包括数值、括号以及操作符，将这些标记按顺序存放起来；（2）根据步骤1所得的标记，根据四则运算规则将其转换成一棵语法树（二叉树）；（3）使用后序遍历步骤2所得语法树，按操作进行求值，得出最后结果。程序的整个核心在于语法树如何建立。

三、语法树的建立：

如：10+(5+9)/3-7*3可以解析得如下语法树：

 

使用后序遍历方式对语法树进行遍历，可以得出其值; 

尽管上面的语法树是正确的，构建上面的语法树却不是那么简单，因为在此过程中，我们需要考虑：如何使得一对括号内的数值作为一个整体优先被计算？ 如果只是按操作符的优先级进行比较，那么我们很可能得出错误的结论。比如上述的表达式换成“10+（5+9）+7*3”，在构建完“10+（5+9）+”的语法树后，此时所得的树根是“10+（”中的“+”，它的运算优先级比“7*3”中的“*”的优先级要低，如果只是按照运算符优先级规则，我们很可能得一棵错误的语法树！因此，我们要简化对问题的思考方式，如何将一个有括号的表达式转换成一个没有括号的表达式，这样，我们只须考虑操作符的优先级就可以创建正确的语法树了！方法很简单，我们首先将没有嵌套的括号内的表达式进行解析，然后对它求值，将其结果作为一个数值结点替换原来的括号表达式，如果括号外部有括号，则按上述方法重复进行，直到去掉所有括号为止。如上面的“10+（5+9）/3+（7*3）”可以转换成：“10+14/3+21”，这样就很容易创建语法表达式了。

测试:

 

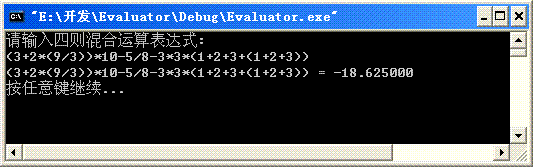
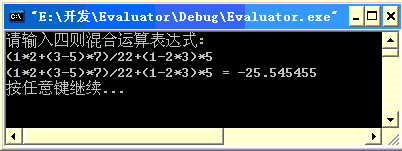
核心代码如下：

// -----------------------------------------------------------------------------
//  语法解析器的实现：
// -----------------------------------------------------------------------------

//  对一个语法树进行求值
double  SyntaxParser::Eval(SYNTAX_TREE tr,  int   & step, FILE *  pf)
... {
  double rslt = 0.0;

  if (0 == tr)  return rslt;

  if (tr->token->GetType() == Token::NUM) 
  ...{
    return (static_cast<Number*>(tr->token))->value;
  }

  double lsh = Eval(tr->lchild, step, pf);
  double rsh = Eval(tr->rchild, step, pf);
  Operator *pop = static_cast<Operator*>(tr->token);
  rslt = Operator::Calc(lsh, rsh, pop->value);

  // 写入计算过程
  fprintf(pf, 
    "%04d.  %-20.6f %-10c %-20.6f = %-20.6f ",
    step,
    lsh, 
    static_cast<char>(pop->value), 
    rsh, 
    rslt);
  ++step;
  return rslt;
}



// ----------------------------------------------------------------------------
//  对输入标记进行解析并求值
//    为简化解析过程，整个表达式可以看作是只有操作符和数值构成的标记表，
//   括号内的表达式可以在解析后进行求值，将所得的结果作为一个数值加点替
//  换原来的括号表达式。因此，整过解析过程中只需考虑操作符的优先级，遇
//  到括号时，作为一棵子树的新解析开始。表达式中只有+,-,*,/ 这个四个操作符。
//  +和-以及*和/它们的优先级是分别相等的。*、/和优先级高于+、-。
// ----------------------------------------------------------------------------
double  SyntaxParser::Solve(
                           TokenTable  & table,   //  标记表
                           TreeStack  & stack,    //  语法树栈
                           EvalFactory  & fac,    //  标记和树结点工厂
                           FILE  * pf             //  计算过程记录文件
                           )
... { 
  if (table.GetCount()==0) 
  ...{
    throw Exception("输入表达式不能为空!");
  }

  typedef Token::TokenType TokenType;
  SYNTAX_TREE tree = 0;           // 语法树
  int parSignal = 0;              // 括号配对信号量，解析结束时若parSignal须为0
  int step = 1;                   // 计算步骤
  Token* prevTok = 0;             // 前一标记
  Token* firstTok = table[0];     // 第一个标记
  Token* lastTok = table[table.GetCount()-1]; // 最后一个标记

  // 首先检查首尾是否正确
  if ((Token::OPER==firstTok->GetType() || Token::OPER==lastTok->GetType())
    || ((Token::LRP==firstTok->GetType() 
    && (static_cast<Parenthesis*>(firstTok))->value!=Parenthesis::LP))
    || ((Token::LRP==lastTok->GetType() 
    && (static_cast<Parenthesis*>(lastTok))->value!=Parenthesis::RP)))
  ...{
    throw Exception("无效表达式! 开头或结尾有误!");
  }


  // 从标记表中提取每个标记，生成语法树
  for (int i=0; i<table.GetCount(); ++i)
  ...{
    Token* token = table[i];

    if (token->GetType()==Token::LRP) // 如果输入标记是括号
    ...{
      Parenthesis* pp = static_cast<Parenthesis*>(token);
      if (Parenthesis::LP == pp->value)  // 当前标记是一个左括号
      ...{
        if (prevTok && prevTok->GetType() != Token::OPER
          && (Token::LRP==prevTok->GetType() 
          &&(static_cast<Parenthesis*>(prevTok))->value!=Parenthesis::LP))
        ...{
          throw Exception("无效表达式:'('之前只能为操作符或'('");
        }

        ++parSignal; // 信号量递增
        stack.Push(tree);
        tree = 0;
      }
      else // 当前标记是一个右括号
      ...{
        if (prevTok && (prevTok->GetType()==Token::OPER
          || (prevTok->GetType()==Token::LRP 
          && (static_cast<Parenthesis*>(prevTok))->value==Parenthesis::LP)))
        ...{
          throw Exception("无效表达式:')'之前只能为数或')'");
        }

        if (parSignal == 0) ...{ // 检查左右括号是否匹配
          throw Exception("无效表达式:'('和')'不匹配!");
        }

        // 将已解析的括号内的子树进行计算，将结果作为一个数值结点插入到语法树中
        SYNTAX_TREE_NODE *pnode = fac.CreateSyntaxTreeNode();
        Number *pnum = static_cast<Number*>(fac.CreateToken(Token::NUM));
        pnum->value = Eval(tree, step, pf);
        pnode->lchild = pnode->rchild = 0;
        pnode->token = pnum;

        SYNTAX_TREE tr = (stack.IsEmpty() ? 0 : stack.Pop());
        if (tr) 
        ...{
          if (tr->rchild) ...{
            tr->rchild->rchild = pnode;
          }
          else ...{
            tr->rchild = pnode;
          }
          tree = tr;
        }
        else ...{
          tree = pnode;
        }

        --parSignal; // 信号量递减
      }
    }
    else // 如果输入标记是操作符或数值
    ...{
      SYNTAX_TREE_NODE *pnode = fac.CreateSyntaxTreeNode();
      pnode->lchild = pnode->rchild = 0;
      pnode->token = token;

      if(token->GetType() == Token::OPER) // 如果输入标记是操作符
      ...{
        // 判断上下文是否有效
        if (prevTok->GetType()==Token::OPER
          || (prevTok->GetType()==Token::LRP 
          && (static_cast<Parenthesis*>(prevTok))->value!=Parenthesis::RP))
        ...{
          throw Exception("无效表达式:操作符之前只能是')'或一个数!");
        }

        Operator *pop = static_cast<Operator*>(token);
        if (tree->token->GetType() == Token::NUM) // 当前树根结点的类型为数
        ...{
          pnode->lchild = tree;
          tree = pnode;
        }
        else  // 当前树根结点的类型操作符
        ...{
          // 如果当前节点优先级高于当前树根结点的优先级, 替换右子树
          if (pop->Compare(static_cast<const Operator&>(*tree->token)) > 0)
          ...{
            pnode->lchild = tree->rchild;
            tree->rchild = pnode;
          }
          else
          ...{
            pnode->lchild = tree;
            tree = pnode;
          }
        }
      }
      else // 如果当前标记是数值
      ...{
        if (prevTok && ((prevTok->GetType()==Token::LRP
          && (static_cast<Parenthesis*>(token))->value==Parenthesis::RP)
          || prevTok->GetType() == Token::NUM))
        ...{
          throw Exception("无效表达式: 数之前只能是操作符或'('!");
        }

        if (0 == tree)
        ...{
          tree = pnode;
        }
        else
        ...{
          SYNTAX_TREE tr = tree;
          if (tr->rchild) ...{
            tr->rchild->rchild = pnode;
          } 
          else ...{
            tr->rchild = pnode;
          }
        }
      }
    }
    // 记录当前标记, 因为解析过程是上下文相关的
    prevTok = token;
  }

  // 检查左右括号数是否匹配
  if (parSignal != 0) ...{ 
    throw Exception("'('和')'的个数不匹配！");
  }

  // 若树栈不为空，则依次弹出一个树tree, 将root作为tree的右孩子，
  // 然后将tree保存到树根root;
  while(!stack.IsEmpty())
  ...{
    SYNTAX_TREE tr = stack.Pop();
    if (tr) ...{
      tr->rchild = tree;
      tree = tr;
    }
  }

  return Eval(tree, step, pf);
}

 

关于分析程序的具体实现，请下载代码： http://download.csdn.net/source/341787