动态规划总结

funNLPer

已于 2024-02-25 21:21:56 修改

阅读量287

点赞数

分类专栏：数据结构算法文章标签：算法动态规划

于 2020-02-11 22:18:14 首次发布

本文链接：https://blog.csdn.net/orangerfun/article/details/104270623

版权

数据结构算法专栏收录该内容

13 篇文章 1 订阅

订阅专栏

文章目录

1.动态规划三大步骤
2. 案例详解
- 2.1 案列一：简单一维DP
- 2.2 案例二：二维数组的 DP
3. 经典例题
4. 参考

1.动态规划三大步骤

动态规划，无非就是利用历史记录，来避免我们的重复计算。而这些历史记录，我们得需要一些变量来保存，一般是用一维数组或者二维数组来保存。下面我们先来讲下做动态规划题很重要的三个步骤

(1) 定义数组元素的含义
上面说了，我们会用一个数组，来保存历史数组，假设用一维数组 dp[] 吧。这个时候有一个非常非常重要的点，就是规定你这个数组元素的含义，例如你的 dp[i] 是代表什么意思？

(2) 找出数组元素之间的关系式
有一点类似于我们高中学习时的归纳法的，当我们要计算 dp[n] 时，是可以利用 dp[n-1]，dp[n-2]……dp[1]，来推出 dp[n] 的，也就是可以利用历史数据来推出新的元素值，所以我们要找出数组元素之间的关系式，例如 dp[n] = dp[n-1] + dp[n-2]，这个就是他们的关系式了。

(3) 找出初始值
数学归纳法的都知道，虽然我们知道了数组元素之间的关系式，例如 dp[n] = dp[n-1] + dp[n-2]，我们可以通过 dp[n-1] 和 dp[n-2] 来计算 dp[n]，但是，我们得知道初始值啊，例如一直推下去的话，会由 dp[3] = dp[2] + dp[1]。而 dp[2] 和 dp[1] 是不能再分解的了，所以我们必须要能够直接获得 dp[2] 和 dp[1] 的值，而这，就是所谓的初始值。

有了初始值，并且有了数组元素之间的关系式，那么我们就可以得到 dp[n] 的值了，而 dp[n] 的含义是由你来定义的，你想求什么，就定义它是什么，这样，这道题也就解出来了。

2. 案例详解

2.1 案列一：简单一维DP

问题描述
一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法

(1) 定义数组元素的含义
先我们来定义 dp[i] 的含义，我们的问题是要求青蛙跳上 n 级的台阶总共由多少种跳法，那我们就定义 dp[i] 的含义为：跳上一个 i 级的台阶总共有 dp[i] 种跳法。这样，如果我们能够算出 dp[n]，不就是我们要求的答案吗？

(2) 找出数组元素间的关系式
我们的目的是要求 dp[n]，动态规划的题，如你们经常听说的那样，就是把一个规模比较大的问题分成几个规模比较小的问题，然后由小的问题推导出大的问题。也就是说，dp[n] 的规模为 n，比它规模小的是 n-1, n-2, n-3…. 也就是说，dp[n] 一定会和 dp[n-1], dp[n-2]….存在某种关系的
对于这道题，由于青蛙可以选择跳一级，也可以选择跳两级，所以青蛙到达第 n 级的台阶有两种方式

一种是从第 n-1 级跳上来

一种是从第 n-2 级跳上来

由于我们是要算所有可能的跳法的，所以有 dp[n] = dp[n-1] + dp[n-2]。

(3) 找出初始条件
当 n = 1 时，dp[1] = dp[0] + dp[-1]，而我们是数组是不允许下标为负数的，所以对于 dp[1]，我们必须要直接给出它的数值，相当于初始值，显然，dp[1] = 1。一样，dp[0] = 0.（因为 0 个台阶，那肯定是 0 种跳法了）。于是得出初始值：

dp[0] = 0.
dp[1] = 1.
即 n <= 1 时，dp[n] = n.
注意：当 n = 2 时，dp[2] = dp[1] + dp[0] = 1。这显然是错误的，你可以模拟一下，应该是 dp[2] = 2

所以该题的动态规划程序为：

int f( int n ){
    if(n <= 1)
    return n;
    // 先创建一个数组来保存历史数据
    int[] dp = new int[n+1];
    // 给出初始值
    dp[0] = 0;
    dp[1] = 1;
    dp[2] = 2
    // 通过关系式来计算出 dp[n]
    for(int i = 3; i <= n; i++){
        dp[i] = dp[i-1] + dp[i-2];
    }
    // 把最终结果返回
    return dp[n];
}

2.2 案例二：二维数组的 DP

DP 的算法题，可以说，80% 的题，都是要用二维数组的，所以下面的题主要以二维数组为主

问题描述
一个机器人位于一个 m x n 网格的左上角 （起始点在图中标记为“Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
问总共有多少条不同的路径？

（1）定义数组元素的含义
由于我们的目的是从左上角到右下角一共有多少种路径，那我们就定义 dp[i] [j]的含义为：当机器人从左上角走到(i, j) 这个位置时，一共有 dp[i] [j] 种路径。那么，dp[m-1] [n-1] 就是我们要的答案了。

（2）找出关系数组元素间的关系式
由于机器人可以向下走或者向右走，所以有两种方式到达

一种是从 (i-1, j) 这个位置走一步到达

一种是从(i, j - 1) 这个位置走一步到达

因为是计算所有可能的步骤，所以是把所有可能走的路径都加起来，所以关系式是 dp[i] [j] = dp[i-1] [j] + dp[i] [j-1]。

（3）找出初始值
显然，当 dp[i] [j] 中，如果 i 或者 j 有一个为 0，那么还能使用关系式吗？答是不能的，因为这个时候把 i - 1 或者 j - 1，就变成负数了，数组就会出问题了，所以我们的初始值是计算出所有的 dp[0] [0….n-1] 和所有的 dp[0….m-1] [0]。这个还是非常容易计算的，相当于计算机图中的最上面一行和左边一列。因此初始值如下：

dp[0] [0….n-1] = 1; // 相当于最上面一行，机器人只能一直往左走

dp[0…m-1] [0] = 1; // 相当于最左面一列，机器人只能一直往下走

代码为：

public static int uniquePaths(int m, int n) {
    if (m <= 0 || n <= 0) {
        return 0;
    }

    int[][] dp = new int[m][n]; // 
      // 初始化
      for(int i = 0; i < m; i++){
      dp[i][0] = 1;
    }
      for(int i = 0; i < n; i++){
      dp[0][i] = 1;
    }
        // 推导出 dp[m-1][n-1]
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
        }
    }
    return dp[m-1][n-1];
}

在这就讲两个稍微简单的例题，更多例题见LeetCode题库，github上也有一些动态规划讲解【click here】

3. 经典例题

3.1 最小路径

题目描述
给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小；每次只能向下或者向右移动一步

输入:grid = 
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
          ]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

思路
由于我们的目的是从左上角到右下角，最小路径和是多少，那我们就定义 dp[i] [j]的含义为：当机器人从左上角走到(i, j) 这个位置时，最小的路径和是 dp[i] [j]。那么，dp[m-1] [n-1] 就是我们要的答案了。
显然有

p[i] [j] = min(dp[i-1][j]，dp[i][j-1]) + arr[i][j];// arr[i][j] 表示网格种的值

找出初始值

dp[0] [j] = arr[0] [j] + dp[0] [j-1]; // 相当于最上面一行，机器人只能一直往左走
dp[i] [0] = arr[i] [0] + dp[i] [0];  // 相当于最左面一列，机器人只能一直往下走

完整程序

public static int uniquePaths(int[][] arr) {
      int m = arr.length;
      int n = arr[0].length;
    if (m <= 0 || n <= 0) {
        return 0;
    }

    int[][] dp = new int[m][n]; // 
      // 初始化
      dp[0][0] = arr[0][0];
      // 初始化最左边的列
      for(int i = 1; i < m; i++){
      dp[i][0] = dp[i-1][0] + arr[i][0];
    }
      // 初始化最上边的行
      for(int i = 1; i < n; i++){
      dp[0][i] = dp[0][i-1] + arr[0][i];
    }
        // 推导出 dp[m-1][n-1]
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + arr[i][j];
        }
    }
    return dp[m-1][n-1];
}

3.2 编辑距离

题目描述
给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数。你可以对一个单词进行如下三种操作：
插入一个字符
删除一个字符
替换一个字符

示例 1:
输入: word1 = "horse", word2 = "ros"
输出: 3
解释: 
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

思路
（1）定义数组元素的含义
定义 dp[i][j] 的含义为：当字符串word1的长度为 i，字符串 word2 的长度为 j 时，将 word1 转化为 word2 所使用的最少操作次数为 dp[i] [j]

（2）递推关系式
如果我们 word1[i] 与 word2 [j] 相等，这个时候不需要进行任何操作，显然有 dp[i] [j] = dp[i-1] [j-1] 。
如果我们 word1[i] 与word2 [j] 不相等，这个时候我们就必须进行调整，而调整的操作有 3 种，我们要选择一种。三种操作对应的关系试如下（注意字符串与字符的区别）：

（a）如果把字符 word1[i] 替换成与word2[j]相等，则有 dp[i] [j] = dp[i-1] [j-1] + 1;

（b）、如果在字符串 word1末尾插入一个与 word2[j] 相等的字符，则有 dp[i] [j] = dp[i] [j-1] + 1;

（c）、如果把字符 word1[i] 删除，则有 dp[i] [j] = dp[i-1] [j] + 1;

那么我们应该选择一种操作，使得 dp[i] [j] 的值最小，显然有

dp[i] [j] = min(dp[i-1] [j-1]，dp[i] [j-1]，dp[[i-1] [j]]) + 1

（3）初始值
初始值是计算出所有的 dp[0] [0….n] 和所有的 dp[0….m] [0]。这个还是非常容易计算的，因为当有一个字符串的长度为 0 时，转化为另外一个字符串，那就只能一直进行插入或者删除操作了

完整程序

public int minDistance(String word1, String word2) {
    int n1 = word1.length();
    int n2 = word2.length();
    int[][] dp = new int[n1 + 1][n2 + 1];
    // dp[0][0...n2]的初始值
    for (int j = 1; j <= n2; j++) 
        dp[0][j] = dp[0][j - 1] + 1;
    // dp[0...n1][0] 的初始值
    for (int i = 1; i <= n1; i++) dp[i][0] = dp[i - 1][0] + 1;
        // 通过公式推出 dp[n1][n2]
    for (int i = 1; i <= n1; i++) {
        for (int j = 1; j <= n2; j++) {
              // 如果 word1[i] 与 word2[j] 相等。第 i 个字符对应下标是 i-1
            if (word1.charAt(i - 1) == word2.charAt(j - 1)){
                p[i][j] = dp[i - 1][j - 1];
            }else {
               dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;
            }         
        }
    }
    return dp[n1][n2];  
}

3.3 最长公共子串

求两个字符串中最长连续相同的子串长度

例1：
str1 = "1AB2345CD", str2 = "12345EF",则str1，str2的最长公共子串为2345
例2：
A = "hellowworld"   B="loop",  则A和B的最长公共子串是“lo”

（1）定义数组含义
res[i][j] 是以 A[i] 和 B[j] 为最后一个元素的最长公共子串的长度
以例2 为例：
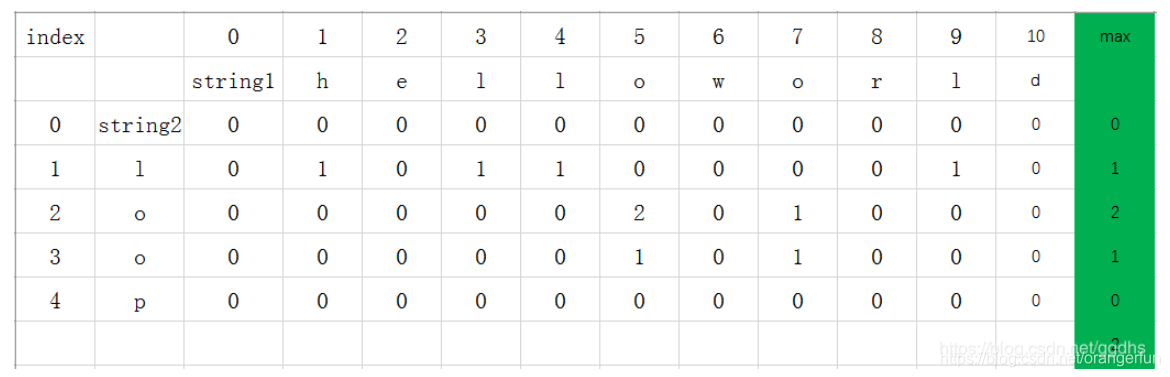
在这里插入图片描述
（2）递推公式

当 i=0 或 j=0，res[i][j] = 0
当 A[i] = B[j]时，res[i][j] = res[i-1][j-1]+1
当 A[i] != B[j]时，res[i][j] = 0

完整程序

def longestString(s1,s2):
	m = [[0 for _ in range(len(s1)+1)] for _ in range(len(s2)+1)]
	flag = 0
	maxlength = 0
	for i in range(1,len(s2)+1):
		for j in range(1,len(s1)+1):
			if s1[j-1] == s2[i-1]:
				m[i][j] = m[i-1][j-1]+1
				# 使用maxlength实时更新最大子串长度
				if maxlength < m[i][j]:
					maxlength = m[i][j]
					# 使用flag记录公共子串结束的索引
					flag = i
			else:
				m[i][j] = 0
	return maxlength, s2[i-maxlength:i]

if __name__ == '__main__':
	string1 = input("please input a string:")
	string2 = input("please input another string:")
	print(longestString(string1,string2))

3.4 最长公共子序列

题目
子序列和子字符串不同，子序列可以是由母字符串中不同位置的元素组成（各元素之间的相对位置不变），子字符串必须是相邻的元素组成

例1：
A = "HellowWord"     B = "Loop"
则 A 和 B 的最长公共子序列为 "loo" ，长度为3

思路
（1）状态定义
res[i][j] 为截止到字符串 A 的第i个元素和字符串B的第j个元素的公共子序列的最大长度
（2）状态转移
如果 A[n] = B[m], 即A、B的最后一个元素相同，则该元素必定在公共子序列中，因此只需找res[n-1][m-1](即A前n-1个元素和B中前m-1个元素的最长公共子序列)
如果 A[n] != B[m], 将产生两个子问题，res[n-1][m]和res[n][m-1],此时最大子序列就在两者之间查找即max{res[n-1][m], res[n][m-1]}

when i = 0 or j = 0, res[i][j] = 0;
when A[i] = B[j], res[i][j] = res[i-1][j-1] + 1;
when A[i] != B[j], res[i][j] = max{res[i][j-1], res[i-1][j]}

（3）如何找到具体子序列
假设有如下两个字符串： S1 = “123456778” S2 = “357486782” 其最终的动态规划填表结果如下：
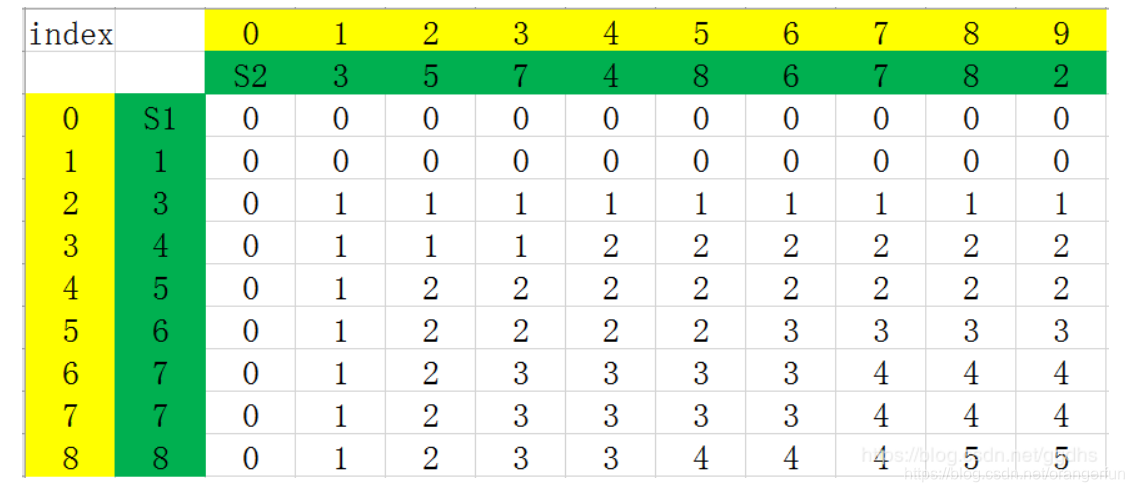
在这里插入图片描述
根据上面的状态转移公式，从最后一个元素到推出S1和S2的LCS(最长公共子序列)

res[8][9] = 5，且S1[8] != S2[9]，所以倒推回去，res[8][9]的值来源于c[8][8]的值(因为res[8][8] > res[7][9])
res[8][8] = 5, 且S1[8] = S2[8], 所以倒推回去，res[8][8]的值来源于 res[7][7]
以此类推，如果遇到S1[i] != S2[j] ，且res[i-1][j] = res[i][j-1] 这种存在分支的情况，这里都选择一个方向（之后遇到这样的情况，也选择相同的方向，要么都往左，要么都往上）

使用上面方法可以得到如下递推图
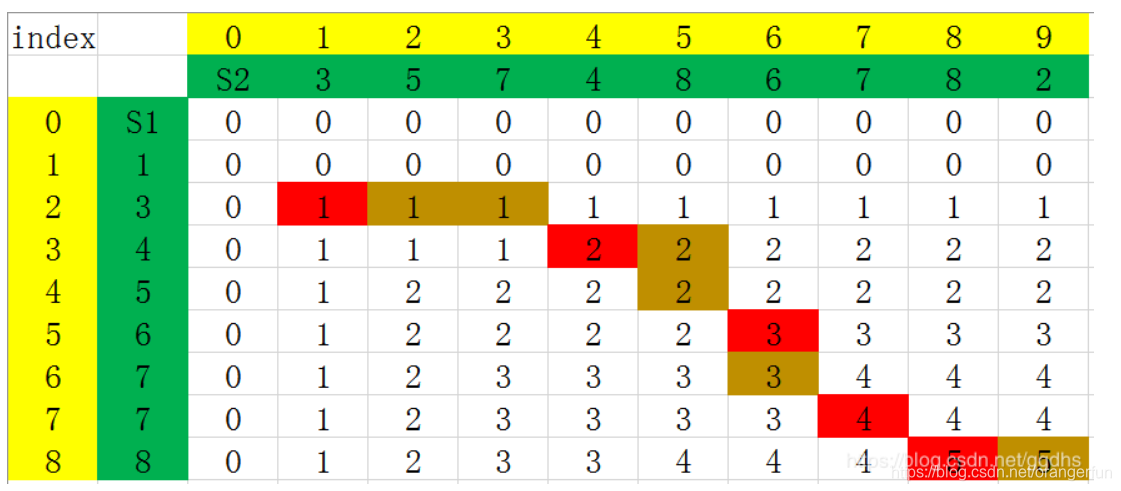
在这里插入图片描述
注意：红色方块就是最长子序列中的元素，他们一起组成最长子序列
在从最后一个元素向前寻找最长子序列时，首先将方向固定（如都选择向上），然后当碰到s1[i]==s2[j]时，将该元素append到列表中，当遍历完整个表时，将该列表reverse就得到最长公共子序列

完整程序

def LCS(s1, s2):
	#定义两个矩阵，一个用于计算最长子序列；一个用于最后回溯求解最长子序列（记录方向）
	m = [[0 for _ in range(len(s1)+1)] for j in range(len(s2)+1)]
	flag = [["q" for _ in range(len(s1)+1)] for j in range(len(s2)+1)]

	for i in range(len(s2)):
		for j in range(len(s1)):
			if s1[j] == s2[i]:
				m[i+1][j+1] = m[i][j] + 1
				flag[i+1][j+1] = "done"

			elif s1[j] != s2[i] and (m[i][j+1]>m[i+1][j]):
				m[i+1][j+1] = m[i][j+1]
				flag[i+1][j+1] = "up"

			elif s1[j] != s2[i] and (m[i][j+1] <= m[i+1][j]):
				m[i+1][j+1] = m[i+1][j]
				flag[i+1][j+1] = "left"
	# print(m)
	# print(flag)

	i, j = len(s2), len(s1)
	result = []
	while m[i][j]:
		if flag[i][j] == "done":
			result.append(s1[j-1])
			i -= 1
			j -= 1

		elif flag[i][j] == "left":
			j -= 1

		elif flag[i][j] == "up":
			i -= 1
	result.reverse()
	return "".join(result)

if __name__ == '__main__':
	s1 = "123456778"
	s2 = "357486782"
	print("result:",LCS(s1, s2))

3.5 最长回文子串

题目描述
给定一个字符串 s，找到 s 中最长的回文子串
注意：回文子串是指一个字符串正着读与反着读都一样

例1：
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案

例2：
输入: "cbbd"
输出: "bb"

思路
（1）定义状态
记号 s[L, r] 表示原始字符串的一个子串，L、r 分别是区间的左右边界的索引值，使用左闭、右闭区间表示左右边界可以取到。举个例子，当 s = 'babad' 时，s[0, 1] = 'ba' ，s[2, 4] = 'bad'
dp[L][r] 表示子串 s[L, r]（包括区间左右端点）是否构成回文串，是一个二维布尔型数组

（2）状态转移

当子串只包含 1 个字符，它一定是回文子串
当子串包含 2 个以上字符的时候：如果 s[L, r] 是一个回文串，那么这个回文串两边各往里面收缩一个字符（如果可以的话）的子串 s[L + 1, r - 1] 也一定是回文串，即：如果 dp[L][r] == true 成立，一定有 dp[L + 1][r - 1] = true 成立

因此：给出一个子串 s[L, r] ，如果 s[L] != s[r]，那么这个子串就一定不是回文串如果 s[L] == s[r] 成立，就接着判断 s[L + 1] 与 s[r - 1]，就这样一直循环下去

当原字符串的元素个数为 3 个的时候，如果左右边界相等，那么去掉它们以后，只剩下 1 个字符，它一定是回文串，故原字符串也一定是回文串
当原字符串的元素个数为 2 个的时候，如果左右边界相等，那么去掉它们以后，只剩下 0 个字符，显然原字符串也一定是回文串
由上面两点，只要 s[L + 1, r - 1] 至少包含两个元素，就有必要继续做判断，否则直接根据左右边界是否相等就能得到原字符串的回文性。而“s[L + 1, r - 1] 至少包含两个元素”等价于 L + 1 < r - 1，整理得 L - r < -2，或者 r - L > 2

完整程序

def longestPalindrome(s):
	size = len(s)
	#当s只有1个或者0个（空）元素时，其本身就是回文串
	if size <= 1:
		return s

	maxlength = 1
	longestline = []

	m= [[False for _ in range(size)] for _ in range(size)]
	for r in range(1,size):
		for l in range(r):
			if s[r] == s[l] and (m[l+1][r-1] or r-l<=2):
				m[l][r] = True
				if r-l+1 >maxlength:
					maxlength = r-l+1
					longestline = s[l:r+1]
	return longestline

if __name__ == "__main__":
	s = input("please input a string:")
	print(longestPalindrome(s))

3.6 正则表达式匹配

给定一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖整个字符串 s的，而不是部分字符串。
说明
s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

输入:
s = "mississippi"
p = "mis*is*p*."
输出: false

思路
（1）状态
设dp[i][j]表示s的前i个字符能否被p的前j个字符匹配
（2）状态转移
(a)s[i]==p[j]或者p[j]=='.'时，dp[i][j]=dp[i-1][j-1]
(b)p[j]=='*' and p[j-1]!=s[i]，dp[i][j]=dp[i][j-2]如下例子：

s= ab
p= abd*

(c) p[j]=='*' and (p[j-1]==s[i]或者p[j-1]==".")时，dp[i][j]=(dp[i][j-2] or dp[i-1][j-1] or dp[i-1][j])因为这种情况下，可能需要匹配一次或者多次，也可能需要匹配零次，如下例子

1. 匹配零次
s=abb
p=abbb*
2.匹配1次
s=abb
p=ab*
3.匹配多次
s=abbbbb
p=ab*

综上，总的状态转移如下：

if s[i]==p[j] or p[j]=='.':      
	dp[i][j]=dp[i-1][j-1]
if p[j]=='*':
	if p[j-1]==s[i] or p[j-1]==".":     
		dp[i][j]=(dp[i][j-2] or dp[i-1][j-1] or dp[i-1][j])
	else:   # p[j-1] != s[i] 的情况    
		dp[i][j]=dp[i][j-2]

完整程序

class Solution:
    def isMatch(self, s, p):
        # 特殊情况处理
        if s==None or p==None:
            return False
        
        # dp矩阵初始化
        dp = [[False for j in range(len(p)+1)]for i in range(len(s)+1)]
        dp[0][0] = True
        for i in range(2,len(p)+1):
        	# 当存在*的时候是可以匹配空字符串，因此特殊处理，没有*时，默认为False
            if p[i-1] == "*":
                dp[0][i] = dp[0][i-2]

        # 动态规划
        for i in range(1, len(s)+1):
            for j in range(1, len(p)+1):
                if s[i-1]==p[j-1] or p[j-1]==".":
                    dp[i][j] = dp[i-1][j-1]
                elif p[j-1]=="*":
                    if p[j-2]==s[i-1] or p[j-2]==".":
                        dp[i][j] = (dp[i][j-2] or dp[i-1][j-1] or dp[i-1][j])
                    else:
                        dp[i][j]=dp[i][j-2]
                        
        return dp[len(s)][len(p)]

if __name__=="__main__":
    s = "mississippi"
    p = "mis*is*p*."
    soulution = Solution()
    result = soulution.isMatch(s, p)
    print(result)

3.7 戳气球

题目描述
有 n 个气球，编号为0 到 n-1，每个气球上都标有一个数字，这些数字存在数组 nums 中。

现在要求你戳破所有的气球。每当你戳破一个气球 i 时，你可以获得 nums[left] * nums[i] * nums[right] 个硬币。这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后，气球 left 和气球 right 就变成了相邻的气球。

求所能获得硬币的最大数量。

输入: [3,1,5,8]
输出: 167 
解释: nums = [3,1,5,8] --> [3,5,8] -->   [3,8]   -->  [8]  --> []
     coins =  3*1*5      +  3*5*8    +  1*3*8      + 1*8*1   = 167

说明：可以假设 nums[-1] = nums[n] = 1，但注意它们不是真实存在的所以并不能被戳破。0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100

思路
回溯法

	TODO...

动态规划
题目说可以认为nums[-1] = nums[n] = 1，那么我们先直接把这两个边界加进去，形成一个新的数组points

问题可以换成：在一排气球points中，请你戳破气球0和气球n+1之间的所有气球（不包括0和n+1），使得最终只剩下气球0和气球n+1两个气球，最多能够得到多少分？

定义dp数组含义
dp[i][j] = x表示，戳破气球i和气球j之间（开区间，不包括i和j）的所有气球，可以获得的最高分数为x

根据这个定义，题目要求的结果就是dp[0][n+1]的值，而 base case 就是dp[i][j] = 0，其中0 <= i <= n+1, j <= i+1，因为这种情况下，开区间(i, j)中间根本没有气球可以戳

我们需要「反向思考」，想一想气球i和气球j之间最后一个被戳破的气球可能是哪一个？
其实气球i和气球j之间的所有气球都可能是最后被戳破的那一个，不防假设为k

你不是要最后戳破气球k吗？那得先把开区间(i, k)的气球都戳破，再把开区间(k, j)的气球都戳破；最后剩下的气球k，相邻的就是气球i和气球j，这时候戳破k的话得到的分数就是points[i]*points[k]*points[j]；而戳破开区间(i, k)和开区间(k, j)的气球最多能得到的分数就是dp[i][k]和dp[k][j]；状态转移如下：

dp[i][j] = dp[i][k] + dp[k][j] + points[i]*points[k]*points[j]

对于一组给定的i和j，我们只要穷举i < k < j的所有气球k，选择得分最高的作为dp[i][j]的值即可

注意
状态转移所依赖的状态必须被提前计算出来，dp[i][j]所依赖的状态是dp[i][k]和dp[k][j]，那么我们必须保证：在计算dp[i][j]时，dp[i][k]和dp[k][j]已经被计算出来了（其中i < k < j）
对于任一dp[i][j]，我们希望所有dp[i][k]和dp[k][j]已经被计算，画在图上就是这种情况：
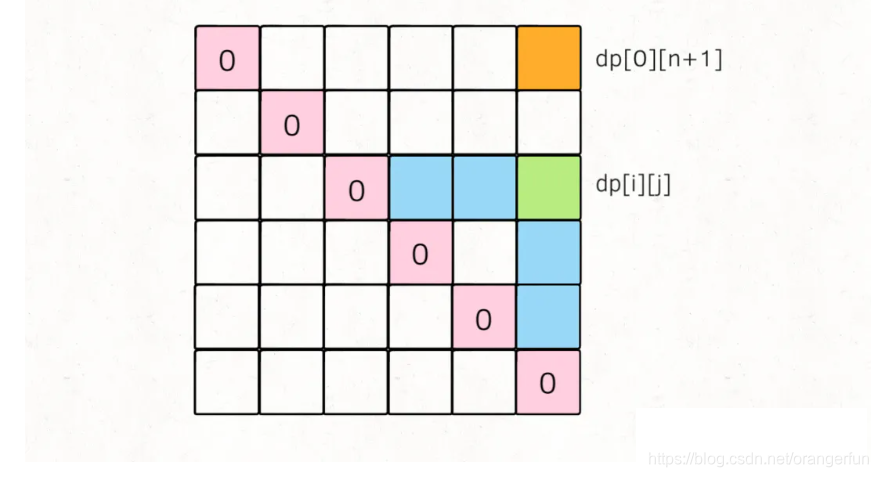
在这里插入图片描述
因此我们需要从下往上遍历

完整程序

class Solution:
    def maxCoins(self, nums: List[int]) -> int:
        length = len(nums)
        coins = [1]*(length+2)
        coins[1:length] = nums
        dp = [[0 for _ in range(length+2)] for _ in range(length+2)]

        for i in range(length, -1, -1):
            for j in range(i+1, length+2):
                for k in range(i+1, j):
                    dp[i][j] = max(dp[i][j], dp[i][k]+dp[k][j]+coins[i]*coins[k]*coins[j])
        return dp[0][length+1]

参考
经典动态规划：戳气球问题

3.8 凑零钱

题目描述
给你k种面值的硬币，面值分别为c1, c2 ... ck，每种硬币的数量无限，再给一个总金额amount，问你最少需要几枚硬币凑出这个金额，如果不可能凑出，算法返回 -1

动态规划
确定dp函数的定义函数 dp(n)表示，当前的目标金额是n，至少需要dp(n)个硬币凑出该金额
明确 base case 显然目标金额为 0 时，所需硬币数量为 0；当目标金额小于 0 时，无解，返回 -1
状态转移

dp[n]=0, n=0
dp[n]=-1, n<0
dp[n] = min([dp[n-coin]+1 for coin in coins])

程序

def solution(amount, coins):
    dp = [amount+1]*(amount+1)
    dp[0] = 0

    for i in range(0, amount+1):
        for coin in coins:
            if i-coin<0:
                continue
            dp[i] = min(dp[i], dp[i-coin]+1)
    return dp[amount] if dp[amount] != amount+1 else -1

if __name__ == '__main__':
    result = solution(10, [1,2,5])
    print(result)

参考
动态规划详解（修订版）

3.9 高楼扔鸡蛋

题目描述
你面前有一栋从 1到N共N层的楼，然后给你K个鸡蛋（K至少为 1）。现在确定这栋楼存在楼层0 <= F <= N，在这层楼将鸡蛋扔下去，鸡蛋恰好没摔碎（高于F的楼层都会碎，低于F的楼层都不会碎）。现在问你，最坏情况下，你至少要扔几次鸡蛋，才能确定这个楼层F呢？

输入：K = 1, N = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，我们肯定知道 F = 0 。
否则，鸡蛋从 2 楼掉落。如果它碎了，我们肯定知道 F = 1 。
如果它没碎，那么我们肯定知道 F = 2 。
因此，在最坏的情况下我们需要移动 2 次以确定 F 是多少。

思路
注意这里两个关键词最坏和最少
假设我们有7层楼，线性扫描：我先在 1 楼扔一下，没碎，我再去 2 楼扔一下，没碎，我再去 3 楼……最坏情况应该就是我试到第 7 层鸡蛋也没碎（F = 7），也就是我扔了 7 次鸡蛋

在第i层楼扔了鸡蛋之后，可能出现两种情况：鸡蛋碎了，鸡蛋没碎。注意，这时候状态转移就来了：
如果鸡蛋碎了，那么鸡蛋的个数K应该减1，搜索的楼层区间应该从[1..N]变为[1..i-1]共i-1层楼；
如果鸡蛋没碎，那么鸡蛋的个数K不变，搜索的楼层区间应该从 [1..N]变为[i+1..N]共N-i层楼
因为我们要求的是最坏情况下扔鸡蛋的次数，所以鸡蛋在第i层楼碎没碎，取决于那种情况的结果更大：
因此可以得到递归程序，递归结束的条件很简单，当楼层数N等于 0 时，显然不需要扔鸡蛋；当鸡蛋数K为 1 时，显然只能线性扫描所有楼层
递归程序

memory = dict()
def recursion(k, n):
# 递归结束条件
    if k==1:
        return n
    if n==0:
        return 0
# 这里我们加入了备忘录，防止重复计算
    if (k, n) in memory:
        return memory[(k, n)]

    res = float("inf")
    for i in range(1, n+1):
        res = min(res, max(recursion(k-1, i-1), recursion(k, n-i))+1)
    memory[(k, n)] = res
    return res

print(recursion(2, 6))

时间复杂度： $O(N*KN)=O(KN^2)$
空间复杂度： $K N$
参考： 经典动态规划：高楼扔鸡蛋

优化1
根据 dp(K, N) 数组的定义（有 K 个鸡蛋面对 N 层楼，最少需要扔几次），很容易知道 K 固定时，这个函数随着 N 的增加一定是单调递增的
那么注意 dp(K - 1, i - 1) 和 dp(K, N - i) 这两个函数，其中 i 是从 1 到 N 单增的，如果我们固定 K 和 N，把这两个函数看做关于 i 的函数，前者随着 i 的增加应该也是单调递增的，而后者随着 i 的增加应该是单调递减的：
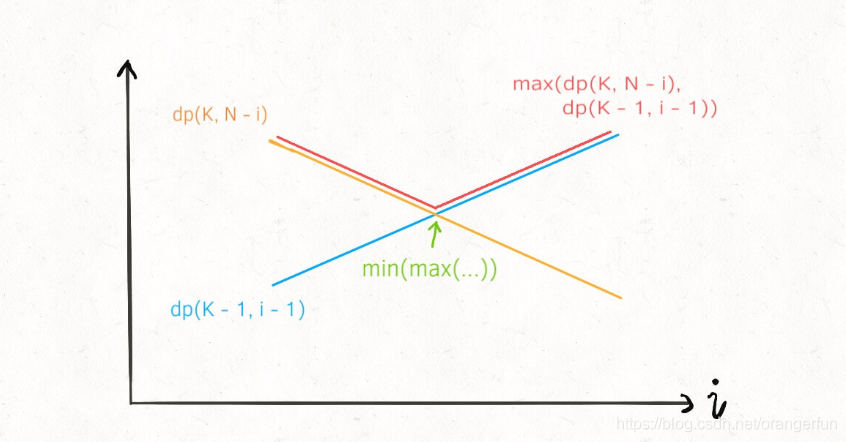
在这里插入图片描述
这时候求二者的较大值，再求这些最大值之中的最小值，其实就是求这两条直线交点，也就是红色折线的最低点
要找的最低点其实就是这种情况:

for (int i = 1; i <= N; i++) {
    if (dp(K - 1, i - 1) == dp(K, N - i))
        return dp(K, N - i);
}

熟悉二分搜索的肯定敏感地想到了，这不就是相当于求 Valley（山谷）值嘛，可以用二分查找来快速寻找这个点的，直接看代码吧，整体的思路还是一样，只是加快了搜索速度：

memory = dict()
def recursion(k, n):
    if k==1:
        return n
    if n==0:
        return 0
    if (k, n) in memory:
        return memory[(k, n)]

    left = 1
    right = n
    res = float("inf")
    
    while left<=right:
        mid = (left+right)//2
        if recursion(k-1, mid-1)<recursion(k, n-mid):
            left = mid+1
            res = min(res, recursion(k, n-mid)+1)
        else: 
            right = mid-1
            res = min(res, recursion(k-1, mid-1)+1)
    memory[(k, n)] = res
    return res
print(recursion(2, 6))

时间复杂度： $O (K Nl o g N)$

优化2
原题目是给你 K 鸡蛋，N 层楼，让你求最坏情况下最少的测试次数 m
现在将题目换个说法：给你 K 个鸡蛋，测试 m 次，最坏情况下最多能测试 N 层楼
有两个事实:

无论你在哪层楼扔鸡蛋，鸡蛋只可能摔碎或者没摔碎，碎了的话就测楼下，没碎的话就测楼上
无论你上楼还是下楼，总的楼层数 = 楼上的楼层数 + 楼下的楼层数 + 1（当前这层楼）

根据这个特点，可以写出下面的状态转移方程：

dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1

dp[k][m - 1] 就是楼上的楼层数，因为鸡蛋个数 k 不变，也就是鸡蛋没碎，扔鸡蛋次数 m 减一；
dp[k - 1][m - 1] 就是楼下的楼层数，因为鸡蛋个数 k 减一，也就是鸡蛋碎了，同时扔鸡蛋次数 m 减1。

def superEggDrop(k, n):
    dp = [[0 for _ in range(n+1)]for _ in range(k+1)]
    m = 0
    while dp[k][m]<n:
        m+=1
        for i in range(1, k+1):
            dp[i][m] = dp[k][m-1]+dp[k-1][m-1]+1
    return m
print(superEggDrop(2,6))

时间复杂度： $O (K N)$

3.10 背包问题

给你一个可装载重量为W的背包和N个物品，每个物品有重量和价值两个属性。其中第i个物品的重量为wt[i]，价值为val[i]，现在让你用这个背包装物品，最多能装的价值是多少？

举个简单的例子，输入如下：

N = 3, W = 4
wt = [2, 1, 3]
val = [4, 2, 3]

算法返回 6，选择前两件物品装进背包，总重量 3 小于W，可以获得最大价值 6

dp[i][w]的定义如下：对于前i个物品，当前背包的容量为w，这种情况下可以装的最大价值是dp[i][w]

在计算dp[i][w]时，如果你没有把这第i个物品装入背包，那么很显然，最大价值dp[i][w]应该等于dp[i-1][w]。你不装嘛，那就继承之前的结果。

如果你把这第i个物品装入了背包，那么dp[i][w]应该等于dp[i-1][w-wt[i-1]] + val[i-1]。

首先，由于i是从1开始的，所以对val和wt的取值是i-1。

而dp[i-1][w-wt[i-1]]也很好理解：你如果想装第i个物品，你怎么计算这时候的最大价值？换句话说，在装第i个物品的前提下，背包能装的最大价值是多少？

显然，你应该寻求剩余重量w-wt[i-1]限制下能装的最大价值，加上第i个物品的价值val[i-1]，这就是装第i个物品的前提下，背包可以装的最大价值。

状态转移

dp[i][w] = max(dp[i-1][w], dp[i-1][w-wt[i-1]]+val[i-1])

完整程序

def bagProblem(N, W, wt, val):
	dp = [[0 for w in range(W+1)] for j in range(N+1)]
	for i in range(1, N+1):
		# 如果背包总重量大于当前物品种量 ，当前物品只能不装
		for w in range(1, W+1):
			if w - wt[i-1]<0:
				dp[i][w] = dp[i-1][w]
			else:
				dp[i][w] = max(dp[i-1][w-wt[i-1]]+val[i-1], dp[i-1][w])
	return dp[N][W]

N, W = 3, 4
wt = [2, 1, 3]
val = [4, 2, 3]
print(bagProblem(N, W, wt, val))

参考
经典动态规划：0-1 背包问题

3.11 分割等和子集

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1:
输入: [1, 5, 11, 5]
输出: true

解释: 数组可以分割成 [1, 5, 5] 和 [11].
 

示例 2:
输入: [1, 2, 3, 5]
输出: false

解释: 数组不能分割成两个元素和相等的子集.

参考
leetcode 416
经典动态规划：0-1背包问题的变体

对于这个问题，我们可以先对集合求和，得出sum，把问题转化为背包问题：
给一个可装载重量为sum/2的背包和N个物品，每个物品的重量为nums[i]。现在让你装物品，是否存在一种装法，能够恰好将背包装满？

状态定义
dp[i][j] = x表示，对于前i个物品，当前背包的容量为j时，若x为true，则说明可以恰好将背包装满，若x为false，则说明不能恰好将背包装满。

根据这个定义，我们想求的最终答案就是dp[N][sum/2]，base case 就是dp[..][0] = true和dp[0][..] = false，因为背包没有空间的时候，就相当于装满了，而当没有物品可选择的时候，肯定没办法装满背包

状态转移
如果不把nums[i]算入子集，或者说你不把这第i个物品装入背包，那么是否能够恰好装满背包，取决于上一个状态dp[i-1][j]，继承之前的结果。

如果把nums[i]算入子集，或者说你把这第i个物品装入了背包，那么是否能够恰好装满背包，取决于状态dp[i - 1][j-nums[i-1]]

动态规划1

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        if sum(nums)%2 != 0:
            return False
        temp = sum(nums)//2

        dp = [[False for i in range(temp+1)] for j in range(len(nums)+1)]
        for i in range(len(nums)+1):
            dp[i][0] = True
        
        for i in range(1, len(nums)+1):
            for j in range(1, temp+1):
                if nums[i-1] > j:
                    dp[i][j] = dp[i-1][j]
                else:
                    dp[i][j] = dp[i-1][j-nums[i-1]] or dp[i-1][j]
        return dp[len(nums)][temp]

状态压缩的动态规划(未懂)

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        temp = sum(nums)
        if temp % 2 != 0:
            return False
        temp = temp//2
        dp = [False]*(temp+1)
        dp[0] = True
        for i in range(len(nums)):
            for j in range(temp, -1, -1):
                if j>=nums[i]:
                    dp[j] = dp[j]|dp[j-nums[i]]
        return dp[temp]

4. 参考

funNLPer

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
1
评论
动态规划总结

1.动态规划三大步骤动态规划，无非就是利用历史记录，来避免我们的重复计算。而这些历史记录，我们得需要一些变量来保存，一般是用一维数组或者二维数组来保存。下面我们先来讲下做动态规划题很重要的三个步骤(1) 定义数组元素的含义上面说了，我们会用一个数组，来保存历史数组，假设用一维数组 dp[] 吧。这个时候有一个非常非常重要的点，就是规定你这个数组元素的含义，例如你的 dp[i] 是代表什么意思...
复制链接

扫一扫