算法系列之十：直线生成算法

最新推荐文章于 2023-02-04 01:20:55 发布

王晓华-吹泡泡的小猫

最新推荐文章于 2023-02-04 01:20:55 发布

阅读量3.1w

点赞数 17

分类专栏：算法系列文章标签：算法图形网格出版扩展工作

本文链接：https://blog.csdn.net/orbit/article/details/7185982

版权

本文介绍了几种常见的直线生成的光栅扫描转换算法，包括数值微分法（DDA法）、Bresenham算法、对称直线生成算法以及两步算法。Bresenham算法因其高效性在计算机图形学中广泛应用，而DDA算法虽然简单但效率较低。对称直线生成算法和两步算法则进一步优化了效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在欧氏几何空间中，平面方程就是一个三元一次方程，直线就是两个非平行平面的交线，所以直线方程就是两个三元一次方程组联立。但是在平面解析几何中，直线的方程就简单的多了。平面几何中直线方程有多种形式，一般式直线方程可用于描述所有直线：

Ax+By+C = 0 （A、B不同时为0）

当知道直线上一点坐标（X₀，Y₀）和直线的斜率K存在时，可以用点斜式方程：

Y-Y₀ = K(X – X₀) （当K不存在时，直线方程简化成X = X₀）

当知道直线上的两个点(X₀,Y₀)和(X₁,Y₁)时，还可以用两点式方程描述直线：

除了这三种形式的直线方程外，直线方程还有截距式、斜截式等多种形式。

在数学范畴内的直线是由没有宽度的点组成的集合，但是在计算机图形学的范畴内，所有的图形包括直线都是输出或显示在点阵设备上的，被成为点阵图形或光栅图形。以显示器为例，现实中常见的显示器（包括CRT显示器和液晶显示器）都可以看成由各种颜色和灰度值的像素点组成的象素矩阵，这些点是有大小的，而且位置固定，因此只能近似的显示各种图形。图（1）就是对这种情况的一种夸张的放大：

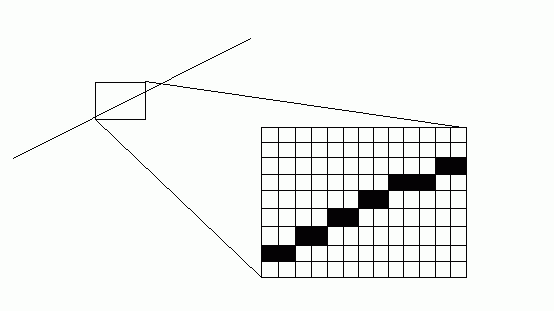
图（1）直线在点阵设备上的表现形式

计算机图形学中的直线生成算法，其实包含了两层意思，一层是在解析几何空间中根据坐标构造出平面直线，另一层就是在光栅显示器之类的点阵设备上输出一个最逼近于图形的象素直线，而这就是常说的光栅图形扫描转换。本文就是介绍几种常见的直线生成的光栅扫描转换算法，包括数值微分法（DDA法）、Bresenham算法、对称直线生成算法以及两步算法。

数值微分法（DDA法）

数值微分画线算法（DDA）法是直线生成算法中最简单的一种，它是一种单步直线生成算法。它的算法是这样的：首先根据直线的斜率确定是以X方向步进还是以Y方向步进，然后沿着步进方向每步进一个点（象素），就沿另一个坐标变量k，k是直线的斜率，因为是对点阵设备输出的，所以需要对每次计算出来的一对坐标进行圆整。

具体算法的实现，除了判断是按照X方向还是按照Y方向步进之外，还要考虑直线的方向，也就是起点和终点的关系。下面就是一个支持任意直线方向的数值微分画线算法实例：

12 void DDA_Line(int x1, int y1, int x2, int y2)
13 {
       
14     double k,dx,dy,x,y,xend,yend;
15 
16     dx = x2 - x1;
17     dy = y2 - y1;
18     if(fabs(dx) >= fabs(dy)) 
19     {
       
20         k = dy / dx;
21         if(dx > 0)
22         {
       
23             x = x1;
24             y = y1;
25             xend = x2;
26         }
27         else
28         {
       
29             x = x2;
30             y = y2;
31             xend = x1;
32         }
33         while(x <= xend) 
34         {
            
35             SetDevicePixel((int)x, ROUND_INT(y)); 
36             y = y + k; 
37             x = x + 1; 
38         }
39 
40     }
41     else
42     {
       
43         k = dx / dy; 
44         if(dy > 0)
45         {
       
46             x = x1;
47             y = y1;
48             yend = y2;
49         }
50         else
51         {
       
52             x = x2;
53             y = y2;
54             yend = y1;
55         }
56         while(y <= yend) 
57         {
            
58             SetDevicePixel(ROUND_INT(</