给一个数列A,长度可达2*10^5,1=<A[i]<=10^6,问数列中任意两个元素Ai,Aj,满足Ai>=Aj时候,Ai%Aj 的最大值是多少
比赛时没做出来,后来过了很久终于理解了。
将A[i]从小到大排序,对于每个A[i],若没访问过,我们访问它2*A[I] , 3*A[I] , ...... ,nA[i],知道nA[I]>maxi为止,maxi为A数列中所有元素最大值
这个复杂度是多少呢?很多人认为有两层for循环,所以是O(n^2),其实不然。分析这个复杂度和素数筛法类似。
我们考虑最坏情况,从1到10^6次方,每个数都从 i, 2i ,3i .... ni, 这样子访问。
假设最大元素是n,那么,对于 1 访问了 n/1 次,对于2,访问了 n/2次,......,对于n,访问了n/n次。所以总体访问时间为:n/1+n/2+n/3+....+n/n次
将n提出来,得到n*(1/1+1/2+1/3+......+1/n),令S=1/1+1/2+1/3+......+1/n,可以证明S与logn是高级无穷小的关系,即S与logn是一个级别的,最多差一个常数
则总体访问时间为nlogn.
将A[i]从小到大排序,对于每个A[i],若没访问过,我们访问它2*A[I] , 3*A[I] , ...... ,nA[i],知道nA[I]>maxi为止,maxi为A数列中所有元素最大值
对于A[I]-2A[i] 中所有数,越靠近2A[i](当然,不可等于)的,其模A[i]的值在这个区间中一定是最大的
对于2A[i]-3A[I]中所有数,越靠近3[I](当然,不可等于)的,其模A[i]的值在这个区间中一定是最大的
......
有了先前的nlogn复杂度分析,我们可以放心的对于每个区间进行二分查找最靠近 nA[i] 的值(当然,不可以等于)
那么,总体复杂度为O(nlognlogn)。不过这是一个可以再优化的做法。在cf上,最快test跑了600-700ms,如果是区域赛丧心病狂的所case数据,可能就会T
怎么样优化成O(nlogn)呢?不难发现,数的范围不大,1=<A[i]<=10^6..用一个数组来记录每个数在A数列中,比它小的第一个数是多少即可,就可以把二分查找O(logn)的步骤转化为数组查询O(1)的步骤了。不过,要注意上界的时候,最后一个数必须要加入讨论。
代码如下:
//Hello. I'm Peter.
#include<cstdio>
#include<iostream>
#include<sstream>
#include<cstring>
#include<string>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<functional>
#include<cctype>
#include<ctime>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
using namespace std;
typedef long long ll;
typedef long double ld;
#define peter cout<<"i am peter"<<endl
#define input freopen("data.txt","r",stdin)
#define randin srand((unsigned int)time(NULL))
#define INT (0x3f3f3f3f)*2
#define LL (0x3f3f3f3f3f3f3f3f)*2
#define gsize(a) (int)a.size()
#define len(a) (int)strlen(a)
#define slen(s) (int)s.length()
#define pb(a) push_back(a)
#define clr(a) memset(a,0,sizeof(a))
#define clr_minus1(a) memset(a,-1,sizeof(a))
#define clr_INT(a) memset(a,INT,sizeof(a))
#define clr_true(a) memset(a,true,sizeof(a))
#define clr_false(a) memset(a,false,sizeof(a))
#define clr_queue(q) while(!q.empty()) q.pop()
#define clr_stack(s) while(!s.empty()) s.pop()
#define rep(i, a, b) for (int i = a; i < b; i++)
#define dep(i, a, b) for (int i = a; i > b; i--)
#define repin(i, a, b) for (int i = a; i <= b; i++)
#define depin(i, a, b) for (int i = a; i >= b; i--)
#define pi 3.1415926535898
#define eps 1e-6
#define MOD 1000000007
#define MAXN 1001000
#define N 200100
#define M
int n,maxi,ans;
int a[N],g[MAXN];
int main()
{
cin>>n;
repin(i,1,n){
scanf("%d",a+i);
g[a[i]]=a[i];
}
sort(a+1,a+1+n);
maxi=a[n];
repin(i,1,maxi){
if(g[i]!=i) g[i]=g[i-1];
}
ans=0;
repin(i,1,n){
if(i&&a[i-1]==a[i]) continue;
for(int j=a[i]<<1;j<=maxi;j+=a[i]){
ans=max(ans,g[j-1]%a[i]);
}
ans=max(ans,maxi%a[i]);
}
printf("%d\n",ans);
}







 本文介绍了一种算法,用于寻找给定整数序列中任意两个元素Ai和Aj(Ai≥Aj)之间的模运算最大值。通过对序列进行排序,并采用特定遍历策略,实现了O(nlogn)的时间复杂度。
本文介绍了一种算法,用于寻找给定整数序列中任意两个元素Ai和Aj(Ai≥Aj)之间的模运算最大值。通过对序列进行排序,并采用特定遍历策略,实现了O(nlogn)的时间复杂度。
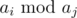 (integer
remainder of
(integer
remainder of 
















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








