算法：计算机几何算法

        这里讨论计算机2D空间内的一些几何算法。讨论的主题包括：两条线段之间的方向、折线在某个顶点上的转向、点是否在线段上的判定、线段是否相交的判定、凸包、给定点组成的多边形是否构成凸多边形的判定、凸多边形面积的计算以及判断点是否在一个多边形(包括凹凸两种多边形) 当中的算法。

        在讨论这些主题之前，首先确定点在计算机内的表示使用一个数对(整数或者浮点数，看具体需求)<X,Y>来表示，而线段使用线段的两个端点来表示。在后面的所有主题讨论之中我们经常会用到一个几何术语：叉积，具体的几何意义表示由两个向量及其平移得到的向量围城的平行四边形的面积，而其算法是这样表示的：向量a=(x1,y1)向量b=(x2,y2)，叉积a×b=x1*y2 + x2*y1；为了这些主题讨论的方便线段l我们有时也会表示成向量，表示的方法是：假设线段l上的两个端点p1(x1,y1),p2(x2,y2)那么表示出来的向量p1p2=(x2-x1,y2-y1)。

一、两条线段的方向

        这个主题要求的就是线段l2在给定线段l1的顺时针或者逆时针方向上。正如上面所说的，我们把两条线段表示成向量的方式，这样转化而来的向量都以共同顶点原点为出发点。这样我们求得两个向量的叉积m，如果m<0说明线段l2在线段l1的逆时针方向上；m>0说明在顺时针方向上；m==0表示两条线段共线。

二、折线在某个顶点上的转向

        假设折线上依次有点p1、p2、p3，求在顶点p2上折线是向左转或者向右转。如图：

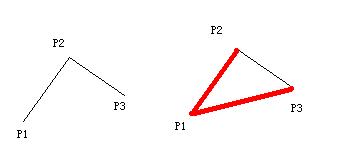
        显然如果我们要求在P2点上的折向我们只需要把P1、P2、P3表示成第二张图上红色部分表示的两个向量P1P2和P1P3，如果向量P1P3在向量P1P2的顺时针方向那么在P2点上就是向右转，否则就是左转，而判断两个向量（或者线段）方向的算法就是第一个主题当中提到的内容。

三、点在线段上的判断

        点是否在线段上的判断有两种方式，第一种计算出线段的方程然后判断，但是这种方式当中由于存在大量除法运算，因此不但效率较差而且存在着精度的问题。而另一种判断方式则是，设线段l上两个顶点p1p2，要求判断的点为p3，我们前面讲到过如果两个向量的叉积为0那么两个向量共线，因此我们首先判断向量p1p3和向量p1p2是否共线，这样我们可以确定点p3是否在线段l确定的直线上，接着我们判断点p3是否在点p1p2确定的矩形当中（判断方式很简单，点p3满足x1<=x3<=x2 && y1<=y3<=y2，切记不可省略两个条件中的任意一个）。

四、判断两条线段是否相交

       这个判断我们当然也可以使用两个线段方程联立求解的方式来判断，但是同样存在性能和精度上的问题。而改进的算法是这样的思想，如果线段l1和l2相交那么线段l1的两个顶点必然在线段l2的两端，同理l2的两个端点也必然在l1的两端，如图：

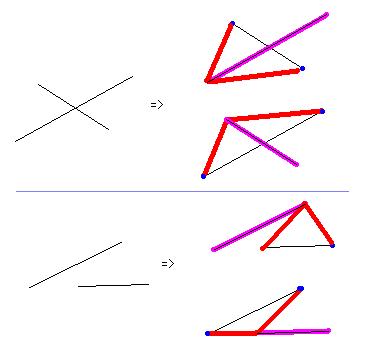
这张图中包括了两种情况相交与不相交，可以看到我们每次都是判断一条线段上的两个点(蓝色表示)是否在另一条线段(用紫色加粗)的两侧，而判断方法很简单，我们使用了两个向量(红色表示)是否在那条线段(紫色加粗)的两端，判断很简单，用叉积，如果两个叉积的积为负表示两个叉积不同号，红色向量在紫色向量的两侧，如果两次判断都满足上面的条件那么可以确定两条线段相交。下面的部分表示了不相交的情况这时求出的两个叉积的积必然为正。当然我们还要考虑下面的边界条件。还是用图来表示

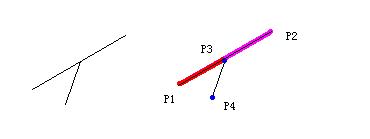
用同样方法来计算叉积的时候在处理叉积m1 = P1P3 * P1P2 与m2 = P1P4 * P1P2时由于m1 == 0 所以 m1*m2 == 0这时说明有线段的端点在另一条线段上的情况出现，通过m1==0我们可以知道P3在线段P1P2上或者在其延长线上，这时需要判断的是点P3是否在线段P1P2上，这时判断回到了第三个主题的情况下。千万要注意的是当叉积等于0的时候并不意味着两条线段相交的情况出现，因为所谓的交点可能出现在延长线上。

五、凸包问题

        所谓凸包就是这样一个问题给定一组点，求用这组点集中的某些点组成的一个最小凸多边形能够包围点集当中所有的点。算法如下：

1、取得一个角点，作为开始点。开始点为最左下点(即y坐标最小，如果有多个相同点则再取x坐标最小)。
2、对所有其他的点，按照倾斜角递增的顺序排序，形成一个闭合的多边形

      这个部分需要注意的有两点，第一、在给对象排序的过程中最重要的是比较两个对象的大小问题，即compareLT(obj1,obj2)算法的实现，在这里由于是按倾斜角来排序，我们可以采用这样的一种比较方式，给定点p1、p2，从原点出发到这两个点的向量也为p1、p2，那么求这两个向量的叉积得到m，如果m<0那么说明向量p2在向量p1的逆时针方向，p2的倾斜角较大，compareLT(p1,p2)应该返回true；第二、对于倾角相同点的处理方式，即m相同的点，对于一组倾角相同的点我们只取其中离第一步当中确定的点距离最远的点，其他的点删除掉。
3、根据第二部排序及预先处理好的一个点集我们以此对除第一步确定的点p0外其他的点做扫描，这里要用到一个堆栈，首先初始化堆栈并将p0以及排序好的点集当中的前两个点入栈，接着扫描剩余的点，每次扫描到一个点则查看堆栈顶部的两个点Pi和Pj，确定在Pi点的转向，如果是向左转则入栈当前点Pm，否则出栈Pi，然后继续查看栈顶两点，比较栈顶点到当前点的转向，知道转向为左Pm点入栈为止。

       这一步当中所说的确定转向部分的算法又回到第二个主题所描述的算法当中。

六、判断给定点所组成的多边形是否为凸多边形

       首先假定给定的点按照某个顺序排定(或者顺时针或者逆时针)，对于给定的点序列<P1,P2,P3,P4...Pm>当中的任意三个点Pi,Pj,Pk，如果满足折线在Pj处的转向都相同(或都为左或都为右)，那么即可判断多边形为凸，判断折线转向的问题又回到主题2所讨论的算法。而事实上如果给定的点位逆时针序，那么转向必然为左；如果为顺时针序必然为右。

七、凸多边形面积的计算

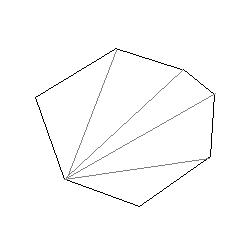
        根据向量叉积的意义我们知道对于三角形P1P2P3，我们求得叉积m=P1P2 * P1P3的绝对值：abs(m)就等于三角形面积的两倍，基于这样的原因我们可以根据给定凸多边形上按逆时针排列的顶点几何选定一点，依次求该点到连续两点组成三角形的面积并最终求和即得到凸多边形的面积，如图：

八、判断点是否在多边形内

        判断点是否在多边形内的方法为将点像左做一条射线(实际只要做一条线段，线段的右端点的x值只要比所有可能点小即可y值与给定点相同)，然后求这条所谓射线与多边形各个边交点的总和count，如果count为偶数则在多边形外否则在多边形内

        但是这里需要注意的是这么几种情况：1.如果多边形的某条边为水平(与X轴平行)则这条边不放入比较；2.如果边与射线的交点在顶点，那么分两种情况，如果该顶点是这条边两个顶点当中y值较大者count++否则count不变；3.如果点P直接在多边形某条边上那么直接判断点在多边形内(当然也要看程序要求)。

        因此该判断的程序流程应该是：

0.count <- 0

1.从多边形依次取出每条边

    Y:有边，转2

    N:无边，转6

2.判断点是否在边上

   Y：返回true

   N：继续

3.判断边是否水平(y1 == y2)

   Y:从1继续执行

   N:继续

4.边的两个顶点是否在射线上

   Y:  4-1-1 判断该顶点是否是y值较大者

              Y:count++;

    N: 判断射线与边是否相交

         Y:count++

5.转1执行

6.结束，输出count