通常聚类算法的结果总是依赖于预先给定的距离度量,而如果预先设定的聚类度量无法抓住数据中的对于使用者来说有用的特征,唯一的挽救方法就是手动地改变距离度量,直到能够得到好的聚类结果了。
如果能有一个系统的方法来帮助使用者告别人工尝试,又能得到合适的距离度量,就是一件很棒的事情了。
因为最近关注谱聚类算法,读到了国内今年初发表的一篇文章,其中就使用了2002年由NJW谱聚类算法的三个设计者其中两个(Andew Y.Ng, Michael I. Jordan)和Eric P. Xing(第一作者)、Stuart Russell提出的一种利用数据的边信息(Side Information)来学习距离度量的方法来提高聚类的准确性。
于是把原始文献翻出来读了一遍,觉得确实有值得思考的地方,就把主要的方法及其思路、实验效果等内容总结一下,写在这里,希望能给读者也带来一些启发吧。
一、聚类中的困扰
聚类嘛,有时候确实是一个让人头疼的问题,因为它可能本就没有正确答案:如果用三个聚类算法来对一些文档组成的集合进行聚类,第一个算法根据作者进行聚类、第二个算法根据主题进行聚类,第三个算法则根据写作风格进行聚类,那么谁能说哪种是正确答案呢?
还可能有更糟糕的情况呢,如果一个算法已经把数据根据主题进行了聚类,而我们现在又想把聚类的方式改为根据写作风格聚类,怎么办呢?——几乎没有什么技术能够帮助我们得到这样神奇的算法,于是仍然只能通过手工改变距离度量(distance metric)来解决。
而这篇文章,就在某种程度上提出了一种解决方案,能够让使用者不必再费心于距离度量的选择,开开心心地玩耍~(≧▽≦)/~啦啦啦~。
文章中,讨论如下的问题:假设用户已经指出在输入空间中(即
Rn
)哪些点被认为是相似的,能否自动地习得
Rn
上的距离度量,使得在该度量下,保持数据点之间的相似关系?(而这些已知的点之间的相似关系,就是待会儿要利用的边信息了。)
好吧,回到刚才的文档分类问题,问题就变成了这样:通过给出哪些被判断为类型相似的文档对,来学习出决定文档类型的关键特征。
其实有一类无监督算法也(潜在地)学习度量,它们利用输入数据集,并找到它到某个空间的一个嵌入。比如说多维尺度分析(MDS, Multidimensional Scaling)和局部线性嵌入(LLE, Local Linear Embedding)。但接下来要谈的方法与它们还是有一定区别的,因为我们不再只关注训练集中的数据(为之找到嵌入),而是从整个输入空间中去学习一个完整的度量。¥因此能够更容易地推广到之前没有学习过的数据上来。
在有监督学习中,为了更好地解决分类问题(如最近邻分类),也有很多寻求局部或全局度量的尝试。这些方法虽然能在分类中学习到不错的度量, 我们却并不知道它们能否适用于其它算法(如K-means),尤其是当可用信息不如它们期望的传统、均匀的训练集那么结构化时。¥
在聚类中,Wagstaff等人提出了一种根据相似信息聚类的方法:如果已经被告知哪些确定的点对是相似或不相似的,这一算法能得到把相似对放到相同聚类、非相似对放到不同聚类的中的聚类结果。但它存在与刚才提到的MDS、LLE类似的缺陷,即无法把结果推广到未经学习的数据上来(如果这些数据与训练集的相似/不相似性是未知的)。¥
二、距离度量的学习
假设我们有一个点的集合
{xi}i=1,...,m⊆Rn
,并且已经知道哪些点之间是相似的:
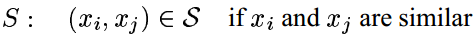
那么如何学习距离度量呢?文章给出的思路是这样的,学习如下形式的距离度量(即马氏距离,Mahalanobis distance):
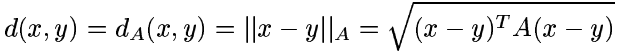
为了确保上式给出的是距离度量(为方便表述,下皆称距离),还要注意到距离应满足的性质(非负性、三角不等式),而这要求矩阵
A
是半正定的,即
注1:当 A=I 时,上述距离就退化为欧式距离;当 A≠I 是对角阵时,上述距离意味着距离对不同的方向赋以不同的权重。事实上,矩阵 A 的习得就对应着将一族马氏距离参数化的过程。
注2:习得上述距离也等价于将输入数据中的每个点
下面我们来为距离的习得设定目标函数了。
一个直接的想法就是,对于已知相似的数据点,要求它们的距离平方和尽量地小,即
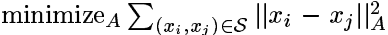
当 A=0 时,问题是平凡的,并且没有实际应用价值,因此我们增加一条限制条件
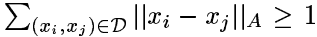 ,以保证矩阵
A
不会把输入数据集聚拢到一个独立点上。当数据信息清晰时,这里的
,以保证矩阵
A
不会把输入数据集聚拢到一个独立点上。当数据信息清晰时,这里的到这里,我们需要求解的优化问题就浮现了:
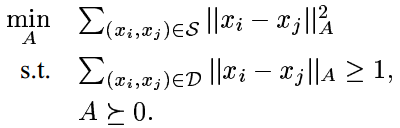
注3:上述第二式右端常数
注4:这一优化问题对于参数 A 来说是线性的,并且两个限制条件都很容易验证是凸的。因此这是一个凸优化问题,这使得我们可以得到高效且避免陷入局部最优解的算法来解决它。
注5:有的人可能会觉得对于限制条件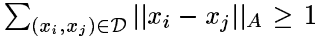
接下来分两种情况讨论矩阵
1.学习对角矩阵
A
这时,希望得到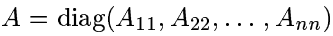
定义
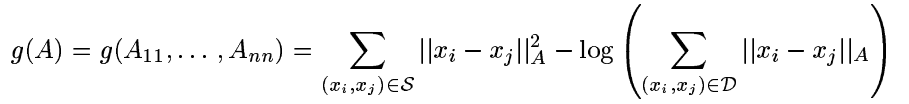
可以知道,最小化函数值 g(A) (满足 A⪰0 )等价于求解刚才我们提到的凸优化问题(至多所得与 A 相差一个正常数倍)。因此可以使用
2.学习一般的矩阵
在这种情况下,
A⪰0
的条件略难满足,
Newton
的方法也不再高效(当参数个数为
n2
时,得到全局最小解的复杂度为
0(n6)
)。这时,使用
梯度上升法和
迭代投射的思想,我们得到一种与刚才不同的算法。
伪代码如下:

注6:上面的
∥⋅∥F
是矩阵的
Frobenius
范数(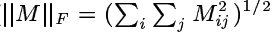
我们提出与之等价的优化问题:
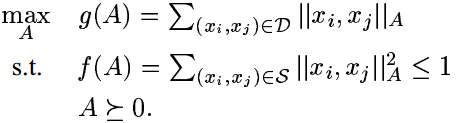
为使第一式函数的值增大,我们对
g(A)
实施梯度上升;接着通过迭代投射的方法来保证满足后两式的限制条件。具体地,梯度上升步骤即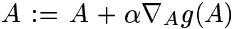
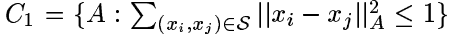
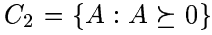
对于这一优化问题,选择上述的形式的限制条件的原因在于,将矩阵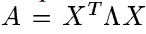
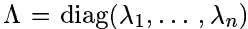
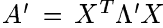
至此,学习距离的方法阐述完毕,可以看一看试验结果了。
三、实验和例子
在这一部分,先展示一下在人工数据集上,距离学习的效果;再看看使用这一方法对于聚类算法有多大的效果增强。
3.1距离学习的例子
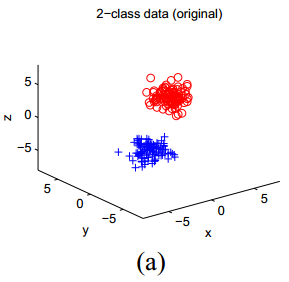
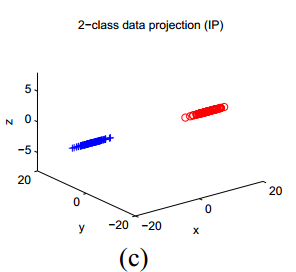
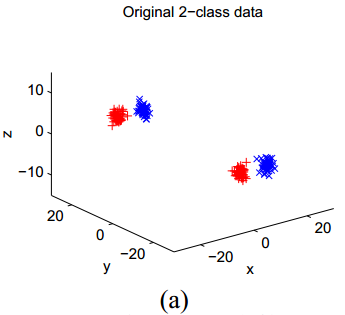
考虑上图(a)中的数据,它们被分为两类(按照不同的颜色和符号展示)。假设每一类中的点之间是相似的,就能根据这一假设来给出点对集合

利用刚才我们提到的对数据重新尺度化数据的方法,可以把这一结果可视化,见上图(b)、(c)。
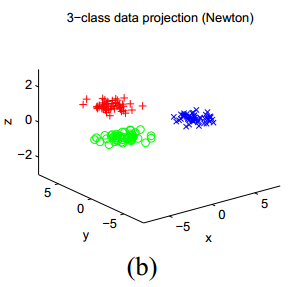
再来看下图,展示了另一组人工数据的结果:
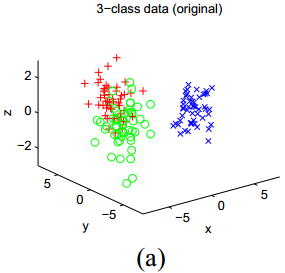
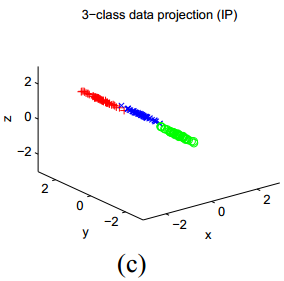
在这一数据中,有3个聚类,它们的中心的坐标在
x
轴和
3.2在聚类中的应用
要把我们提出的距离学习方法应用的聚类上,当然是很简单的一件事情啦~~~在最坏的情况下,我们只要找出一些描述相似点的信息,利用它们构造出包含相似点对的集合
注7 :有时我们还加一个条件,即属于集合 S 中的点对在聚类的结果中仍应该属于同一聚类。
对于K-means算法,现在我们来考虑4个可能的聚类应用:
1.(K-means)使用欧氏距离的标准K-means算法,不考虑集合
2.(Constrained K-means) 使用欧氏距离的标准K-means算法,考虑集合
S
提供的信息,要求属于集合
3.(K-means + metrix) K-means算法,使用通过
S
习得的距离进行聚类
4.(Constrained K-means + metric) K-means算法,使用通过
现在我们要比较这几种不同算法在实际应用中的效果了。
令
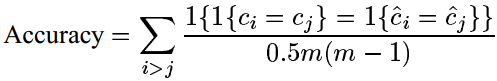
其中 1{⋅} 表示指示函数 1{True}=1,1{False}=0 。这一准确度式子等价于从数据集中随机地抽取出两个点 xi , xj ,聚类算法给出的结果 cˆ 与真实情况 c 符合的概率(无论
下图展示了一个简单的例子。在这一例子中
x
轴的坐标其实就指示了聚类的归属,但是原始数据集看起来更像是按照
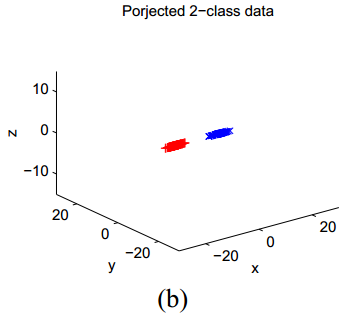
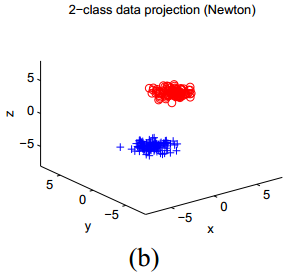
来看一看对这一数据集使用不同的聚类算法,分别得到怎样的结果:

可以看到,使用原始距离的K-means算法得到的聚类效果并不好,但通过距离学习,实现了精确聚类。









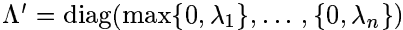
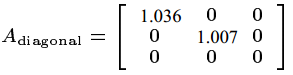













 4072
4072











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








