树状数组的改段求段详解

以下是对于如何利用树状数组进行区间修改和区间查询的简介

可以代替不需要lazy tag的线段树，且代码量和常数较小

首先你需要学会树状数组，如果不会的话以下先讲解黑匣子使用树状数组的姿势

首先定义一个数组 int c[N]; 并清空 memset(c, 0, sizeof c);

1、单点修改 ： c[x] += y; 对应的函数是 change(x, y);

2、求前缀和 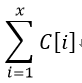：  对应的函数是 int sum(x)

两种操作的复杂度都是O(logn)

模版如下

int c[N], maxn;
inline int Lowbit(int x){return x&(-x);}
void change(int i, int x)//i点增量为x
{
	while(i <= maxn)
	{
		c[i] += x;
		i += Lowbit(i);
	}
}
int sum(int x){//区间求和 [1,x]
	int ans = 0;
	for(int i = x; i >= 1; i -= Lowbit(i))
		ans += c[i];
	return ans;
}

如何运用树状数组进行区间操作

先定义两个树状数组 X, Y

现在我们需要对一个数组 int a[N]; 进行区间操作：[L, R] += val 即 for i:L to R a[i] += val; 

再定义一个 int size = R-L+1 , 即区间长度

对应的修改是 

1、X[L] += val;   X[R+1] -= val;

2、Y[L] += -1 * val * (L-1);   Y[R+1] += val * R;

对应的查询是

当我们求和 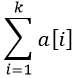 时在树状数组中操作是 ans = X.sum(k) * k + Y.sum(k)

分类讨论一下k分别在 [1,L-1] , [L, R] , [R+1, +]

1、k[1,L-1]  

显然 X.sum(k) == 0 且 Y.sum(k) == 0 -> ans = X.sum(k)*k + Y.sum(k) = 0*i+0 = 0 结果与实际相符。

2、k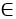[L, R] 

X.sum(k) * k = X[L] * k = val * k,   Y.sum(k) = Y[L] =  -1 * val * (L-1) 

ans = val * k - val * (L-1) = val * ( k - (L-1) ); 

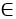
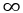
3、k[R+1, ]

X.sum(k) * k = ( x[L] + x[R] ) * k = 0 * k = 0;

Y.sum(k) = Y[L] + Y[R] = -val * (L-1) + val * R = val * (R-L+1) = val * size

X.sum(k) * k + Y.sum(k) = val * size

证毕

以下模版中两个树状数组c[0], c[1] 对应上述的X, Y

区间修改：add(L, R, val)

求 int a[N]的前缀和 get_pre(R)

区间查询：get(L,R)

const int N = 4e5 + 100;
template<class T>
struct Tree{
	T c[2][N];
	int maxn;
	void init(int x){
		maxn = x+10; memset(c, 0, sizeof c);
	}
	inline int lowbit(int x){ return x&-x; }
	T sum(T *b, int x){
		T ans = 0;
		if (x == 0)ans = b[0];
		while (x)ans += b[x], x -= lowbit(x);
		return ans;
	}
	void change(T *b, int x, T value){
		if (x == 0)b[x] += value, x++;
		while (x <= maxn)b[x] += value, x += lowbit(x);
	}
	T get_pre(int r){
		return sum(c[0], r) * r + sum(c[1], r);
	}
	void add(int l, int r, T value){//区间加权
		change(c[0], l, value);
		change(c[0], r + 1, -value);
		change(c[1], l, value * (-l + 1));
		change(c[1], r + 1, value * r);
	}
	T get(int l, int r){//区间求和
		return get_pre(r) - get_pre(l - 1);
	}
};
Tree<ll> tree;