图之最小生成树 Kruskal算法 Prim算法

一.实际问题

最小生成树一般应用在网（带权的图）问题中，实际问题一般比如：
　　假设要在n个城市间建立通信联络网，则联通n个城市只需要n-1条线路，但是每两个城市间都可以建设路线，而且城市与城市间建设代价是不同的，这就需要我们考虑一种经济的联络方式。
将问题转换成图的话，就如下图（圆圈代表城市，线代表线路，线上数值代表建设的代价），我们需要从中选择一条代价最小的建设方式。

二.基本思想

　　一般情况下这类问题归于动态规划中的贪心算法（不一定是但大多数情况下是最优解）。
　　
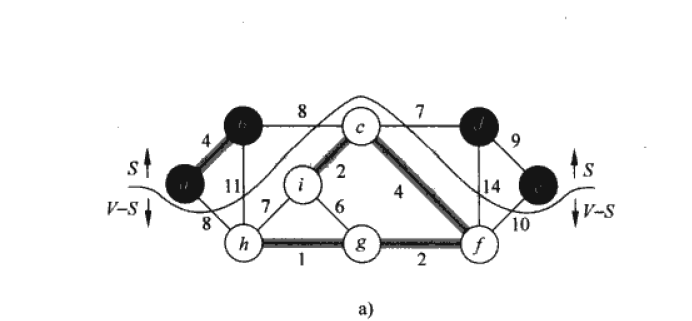
　　跟动态规划一样，我们假设上图弧线以下部分（白色圆圈c，i，h，g，f部分）已经找到最优解的话，那么我们考虑添加一个黑色圆圈时，只需要考虑白色圆圈c，i，h，g，f部分到黑色园圈所有线路中代价最小的线路与黑色园圈相连组成新的子问题最优解（比如白色圆圈c，i，h，g，f部分到最左边黑色圆圈有代价8或11线路，显然我们选择线路代价为8）。接下来介绍的Kruskal和Prim算法其基本思想大抵如此。

三.Kruskal算法

适合求解边稀疏网的最小生成树

克鲁斯卡尔算法首先把每一个节点当成一最小生成棵树，把所有的边从代价小到大排列。
然后逐个选择边（从小到大）：
　　判断边是否连接两个最小生成树，如果能够连接则把两棵最小生成树连接起来生成一个最小生成树； 　　如果这条边连接的是一棵树内两个节点的话就抛弃它，为什么呢？因为我们是从小到大选择的边，如果把当前这条边加入这棵树的话，树内必定会生成一个回路，就需要抛弃一条边，然而先前选择的所有的边都比当前这条边代价小，所以只能抛弃当前这条边。
　　
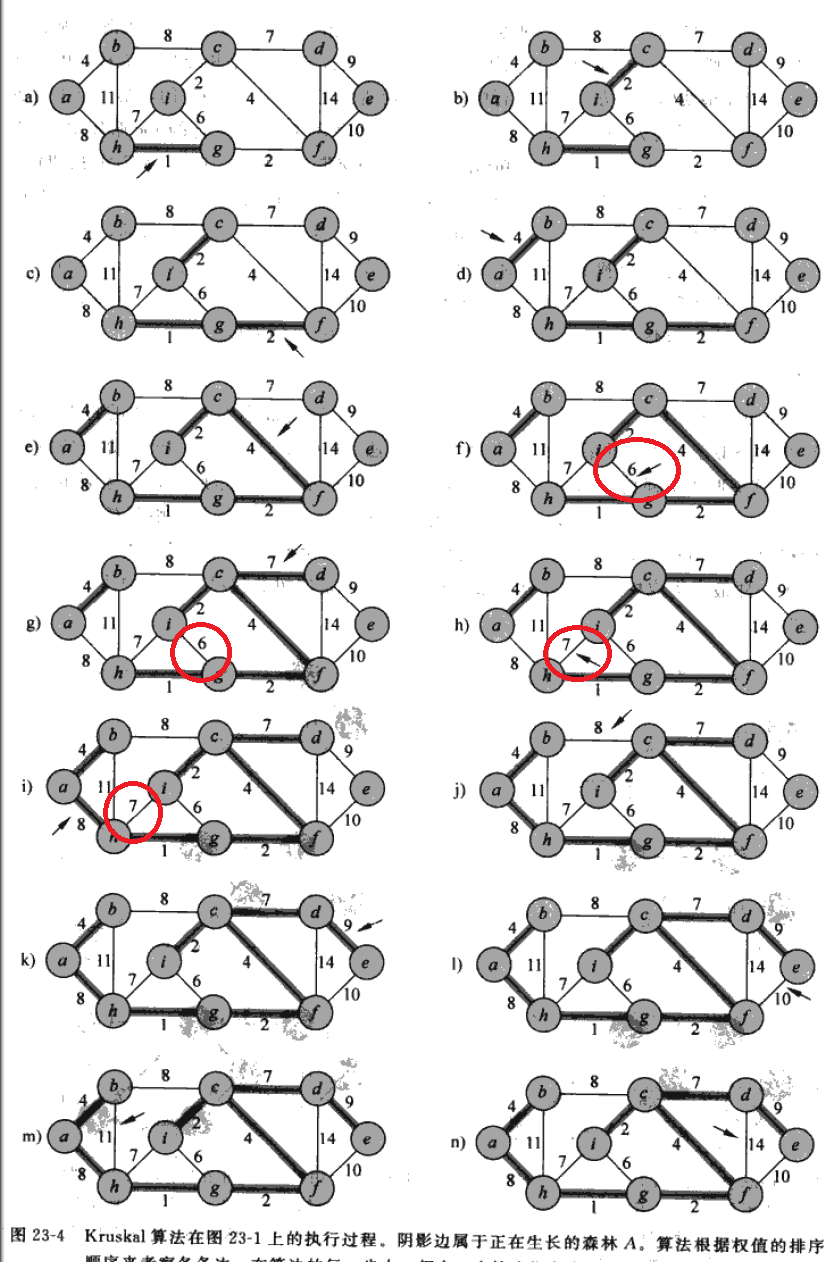
看上述示意图中，红圈部分就是代价高的线路被抛弃了。
算法实例：CCF 地铁修建

四.Prim算法

适合求解边稠密网的最小生成树

普西姆算法与克鲁斯卡尔算法不同，普西姆算法从始到终都只有一棵树。
首先选择任意一个顶点当成一棵树，把（树）和（其他节点）当成两个集合；
然后我们从（其他节点）到（树）线路中选择代价最小的线路，这条线路的端节点必然一个在（树）中，一个在（其他节点）中。把该条最小代价线路在（其他节点）集合中的节点转移到（树）中，从而形成新的最小生成树。重复上述步骤，到最后所有的节点都在（树）集合中。

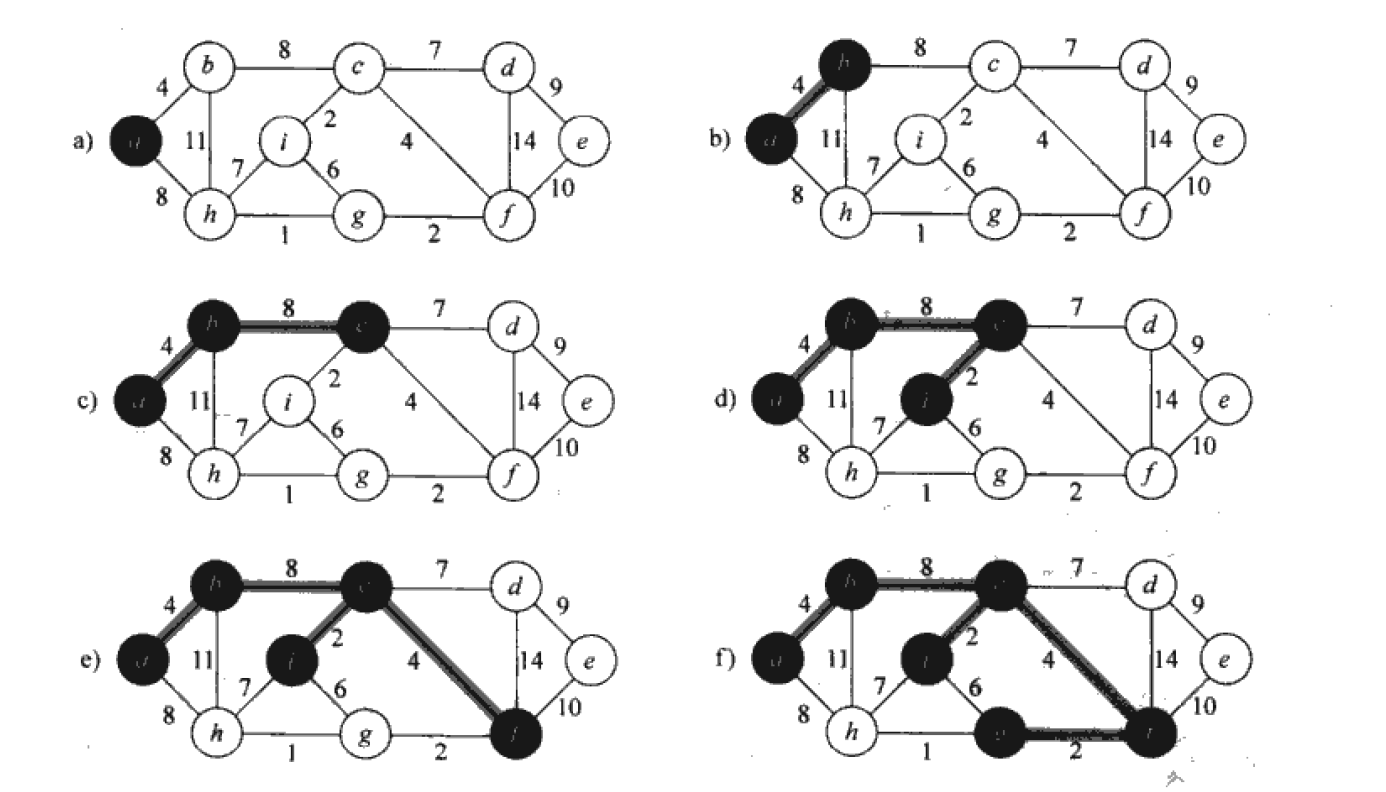
看上述示意图中，始终只有黑色圆圈组成的（树），在只有一个黑点（图1）时，（树）与（其他集合）有两条线路，代价分别为4或8，显然选择4；
然后（树）与（其他集合）间线路就有8或11或8，按贪心算法，我们只需考虑一个子问题，所以选择其中一条代价为8的线路即可。
CCF 最优灌溉
算法实例：CCF 交通规划