回顾前面的知识,我们学了二叉树,而二叉树有很多种存储方式,比如一维数组存储,
链表存储,在刚刚学习建立二叉树的时候,我们用的是链表存储的方式,也就是利用结构体定义一个二
叉树节点,然后将这些节点连接起来。现在为了更好地存储二叉树,我们学习了堆,即将二叉树存储在
一个一维数组里面,由于按照不同的存储顺序,可以将一个堆分为最大堆和最小堆。
最大堆:每个父节点必须大于左右孩子,而每个孩子所代表的子树也是最大堆
最小堆:每个父节点必须小于左右孩子,而每个孩子所代表的子树也是最小堆
那么如何将一个堆变成一个最大堆或者最小堆呢,就是通过向下调整法或者向上调整法,下面会做详细的说明。
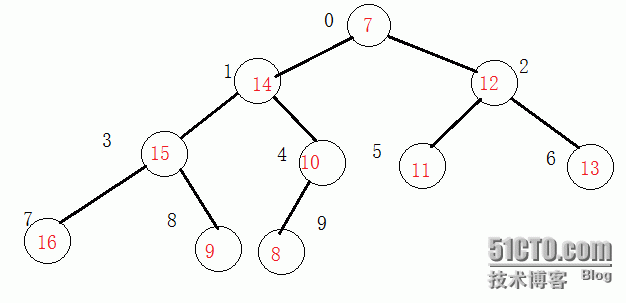
首先我们来举一个栗子,给出如下一棵二叉树:

首先我们需要一个数组将这个二叉树存储起来,因为vector的操作与顺序表相似,为了简便,我们调用
库里的vector来存储二叉树,只不过存储类型为模板类T,此时我们默认建最大堆,所以要提供过向下调
整法来调整,为了使每棵子树都是父节点最大,我们先从最后一个节点找起,然后找到该节点的父节
点,比较父节点和两个子节点的大小,若左右节点有一个比父节点大,则和父节点交换值,然后依次
往前比较,直到整个堆调整为最大堆。
代码如下:
#pragma once
#include<assert.h>
#include<vector>
using namespace std;
template<class T>
class Heap
{
public:
Heap()
{}
//建堆
Heap(const T* a,size_t size)
{
for (size_t i = 0; i < size; i++)//将数组中的数据放到堆里去
{
_a.push_back(a[i]);
}
for (int j = (_a.size() - 2) / 2; j >= 0; j--) //第一个非叶子结点的父亲开始
{
AdjustDown(j);
}
}
protected:
void AdjustDown(size_t parent)
{
int child = parent * 2 + 1;; //找到左孩子
while (child< _a.size())
{
if ((child + 1 < _a.size())&&_a[child] < _a[child + 1] ) //找到左右孩子较大的一个
{
++child;
}
if (_a[child] > _a[parent]) //如果孩子比父亲大,交换孩子和父亲的值
{
swap(_a[child], _a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
protected:
vector<T> _a;
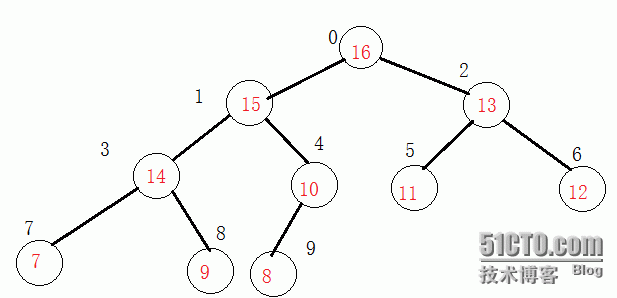
};通过调整整个堆变为最大堆,调整后的二叉树如下所示
那么建立好堆之后,在对数据进行操作的时候对堆也有一定的影响,所以下面我们来简单写一下堆的pop和push。
push:可以直接调用vector的push_back(),然后再通过向上调整法调整变成最大堆
pop:由于vector没有从堆前面直接pop的,所以要将堆的第一个元素与最后一个元素调换位置,再通过pop_back()pop出去,再通过调整变成最大堆。
具体代码如下:
void push(const T& x)
{
_a.push_back(x);
AdjustUp(_a.size() - 1);
}
void pop()
{
assert(!_a.empty());
swap(_a[0], _a[_a.size() - 1]); //由于没有头删函数,将第一个数据和最后一个交换,再尾删
_a.pop_back();
for (int j = (_a.size() - 2) / 2; j >= 0; j--) //调整为最大堆
{
AdjustDown(j);
}
}
protected:
void AdjustDown(size_t parent)
{
int child = parent * 2 + 1;; //找到左孩子
while (child< _a.size())
{
if ((child + 1 < _a.size())&&_a[child] < _a[child + 1] ) //找到左右孩子较大的一个
{
++child;
}
if (_a[child] > _a[parent]) //如果孩子比父亲大,交换孩子和父亲的值
{
swap(_a[child], _a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void AdjustUp(size_t child)
{
int parent = (child - 1) / 2;
while (child>0)
{
if (_a[child]>_a[parent])
{
swap(_a[child], _a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}以上便是堆的建立以及简单的操作,小伙伴们看明白了么?
下面给出测试代码:
#include"Heap.h"
void test()
{
int array[10] = { 7, 14, 12, 15, 10, 11, 13, 16, 9, 8 };
Heap<int> hp1(array, 10);
hp1.push(17);
hp1.pop();
}
int main()
{
test();
return 0;
}由于这里只给出了具体方法,类的成员没有给完全,小伙伴们可以下去自行补全哦,重要的是方法,可能我给出的方法也有一定的不足之处,还希望大家指出共同进步!
本文出自 “福大馨” 博客,转载请与作者联系!





















 2900
2900

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








